
- •Конспект лекций по дисциплине «основы дискретной математики»
- •Лекция № 1. Дискретное и непрерывное
- •Лекция № 2. Системы счисления
- •Лекция № 3. Фракталы
- •3.1. Канторово множество
- •3.2. Ковер Серпинского и снежинка Коха
- •3.3. Стохастические фракталы
- •3.4. Энтропийная размерность
- •3.5. Фрактал Мандельброта
- •Лекция № 4. Основы математической логики
- •Набор истинностных значений 0001 в первой строке таблицы соответствует результатам операций:
- •Основные эквивалентности:
- •X(баскетболист(X)высокий(X))
- •X(личность(х)любит(х, грибы))
- •X любит(х, платить(налоги))
- •X(человек(X)смертный(X)),
- •Лекция № 5. Множества и подмножества
- •Лекция № 6. Математическая индукция
- •Лекция № 7. Комбинаторика
- •Лекция № 8. Числа фибоначчи и простые числа
- •Лекция № 9. Кодирование
- •Лекция № 10. Шифрование
Лекция № 10. Шифрование
Введение
Шифрование – это кодирование данных с целью защиты от несанкционированного доступа. Область знаний о шифрах, методах их создания и раскрытия называется криптографией (или тайнописью).
Криптография известна с глубокой древности и использует самые разнообразные шифры, как чисто информационные, так и механические. В настоящее время наибольшее практическое значение имеет защита данных в компьютере, поэтому далее рассматриваются программные шифры для сообщений в алфавите {0,1}.
Начнем с определения
операции:
![]() .
Здесь операнды:a
и b
– целые числа, а результат данной
операции – остаток, возникающий при
целочисленном делении a
на b.
.
Здесь операнды:a
и b
– целые числа, а результат данной
операции – остаток, возникающий при
целочисленном делении a
на b.
Пример 10.1.
15
![]() 2 =
2 =![]() ,
,
26
![]() 3 =
3 =![]() ,
,
32
![]() 4 =
4 =![]() .
.
Пусть имеется генератор псевдослучайных чисел, работающий по определенному алгоритму. Часто используется следующий алгоритм:
![]() , (10.1)
, (10.1)
где
![]() – предыдущее псевдослучайное число,
– предыдущее псевдослучайное число,![]() – последующее псевдослучайное число,
а коэффициентыa,
b,
c
постоянны и хорошо известны. Обычно
c=
– последующее псевдослучайное число,
а коэффициентыa,
b,
c
постоянны и хорошо известны. Обычно
c=![]() ,
где
,
где![]() – разрядность процессора,
– разрядность процессора,![]() ,
аb
– нечетное. В этом случае последовательность
псевдослучайных чисел имеет период c.
,
аb
– нечетное. В этом случае последовательность
псевдослучайных чисел имеет период c.
Пример 10.2. В
табл. 10.1 приведены результаты расчетов
по формуле (10.1) для различных ключей
шифра
![]() и коэффициентов:a=81,
b=9,
c=65536.
и коэффициентов:a=81,
b=9,
c=65536.
Таблица 10.1
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
90 |
7299 |
1404 |
48197 |
37342 |
10055 |
28032 |
42377 |
24674 |
32523 |
|
10 |
819 |
812 |
245 |
19854 |
35319 |
42800 |
58937 |
55314 |
23995 |
43060 |
|
100 |
8109 |
1478 |
54191 |
64104 |
15089 |
42570 |
40307 |
53612 |
17205 |
17358 |
|
1000 |
15473 |
8138 |
3827 |
47852 |
9397 |
40270 |
50615 |
36592 |
14841 |
22482 |
|
10000 |
23577 |
9202 |
24475 |
16404 |
18013 |
17270 |
22623 |
63000 |
56737 |
8186 |
Процесс шифрования
определяется следующим образом. Шифруемое
сообщение представляется в виде
последовательности слов
![]() ,
каждое длины
,
каждое длины![]() ,
которые складываются по модулю два со
словами последовательности
,
которые складываются по модулю два со
словами последовательности![]() ,
то есть
,
то есть
![]() .
.
Последовательность
![]() называетсягаммой
шифра. Процесс
расшифровывания заключается в том,
чтобы еще раз сложить шифрованную
последовательность с той же самой гаммой
шифра:
называетсягаммой
шифра. Процесс
расшифровывания заключается в том,
чтобы еще раз сложить шифрованную
последовательность с той же самой гаммой
шифра:
![]() .
.
Ключом шифра
является начальное значение
![]() ,
которое является секретным и должно
быть известно только отправителю и
получателю шифрованного сообщения.
Шифры, в которых для зашифровки и
расшифровки используется один и тот же
ключ, называютсясимметричными.
,
которое является секретным и должно
быть известно только отправителю и
получателю шифрованного сообщения.
Шифры, в которых для зашифровки и
расшифровки используется один и тот же
ключ, называютсясимметричными.
Описанный метод
шифрования обладает существенным
недостатком. Если известна хотя бы часть
исходного сообщения, то все сообщение
может быть легко дешифровано. Действительно,
пусть известно одно исходное слово
![]() .
Тогда
.
Тогда
![]() ,
,
и далее вся правая часть гаммы шифра определяется по указанной формуле генератора псевдослучайных чисел.
Для повышения криптостойкости симметричных шифров применяются различные приемы.
Вычисление гаммы шифра по ключу более сложным (или секретным) способом.
Применение вместо
 более сложной (но обратимой операции)
для вычисления шифровки.
более сложной (но обратимой операции)
для вычисления шифровки.Предварительное перемешивание битов исходного сообщения по фиксированному алгоритму.
В настоящее время широкое распространение получили шифры с открытым ключом. Эти шифры не являются симметричными – для зашифровки и расшифровки используются разные ключи. При этом ключ, используемый для зашифровки, является открытым (не секретным) и может быть сообщен всем желающим отправить шифрованное сообщение. А ключ, используемый для расшифровки, является закрытым и хранится в секрете получателем шифрованных сообщений. Даже знание всего зашифрованного сообщения и открытого ключа, с помощью которого оно было зашифровано, не позволяет дешифровать сообщение без знания закрытого ключа.
Для описания метода шифрования с открытым ключом нужны некоторые факты из теории чисел, изложенные (без доказательства) в следующем разделе.
Модулярная арифметика
В этом разделе все
числа – целые. Говорят, что число a
сравнимо по
модулю n
с числом b
(обозначение
![]() ),
еслиa
и b
при делении на n
дают один и тот же остаток:
),
еслиa
и b
при делении на n
дают один и тот же остаток:
![]() .
.
Отношение
сравнимости
рефлексивно, симметрично и транзитивно
и является отношением эквивалентности.
Классы эквивалентности по отношению
сравнимости (по модулю n)
называются вычетами
(по модулю n).
Множество вычетов по модулю n
обозначается
![]() .
Обычно из каждого вычета выбирают одного
представителя – неотрицательное число,
которое при делении наn
дает частное 0. Это позволяет считать,
что
.
Обычно из каждого вычета выбирают одного
представителя – неотрицательное число,
которое при делении наn
дает частное 0. Это позволяет считать,
что
![]() ,
и упростить обозначения.
,
и упростить обозначения.
Над вычетами (по
модулю n)
определены операции сложения и умножения
по модулю n,
обозначаемые соответственно
![]() и
и![]() ,
и определяемые следующим образом:
,
и определяемые следующим образом:
![]() ,
, ![]() .
.
Если из контекста ясно, что подразумевается операция по модулю n, то индекс n опускается.
Рассмотрим
![]() – подмножество
– подмножество![]() чисел,взаимно
простых с
n.
Числа называются взаимно простыми, если
их наибольший общий делитель равен
единице. Для чисел из множества
чисел,взаимно
простых с
n.
Числа называются взаимно простыми, если
их наибольший общий делитель равен
единице. Для чисел из множества
![]() существуют обратные числа по отношению
к операции умножения по модулюn.
существуют обратные числа по отношению
к операции умножения по модулюn.
Пример 10.3.
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
Функция:
![]() – называетсяфункцией
Эйлера.
Если
– называетсяфункцией
Эйлера.
Если
![]() – простое число, то
– простое число, то![]() ,
и вообще
,
и вообще![]() .
.
Можно показать, что
![]() ,
,
где
![]() – все простые делителиn.
– все простые делителиn.
Пример 10.4.
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
Теорема
10.1. (Эйлера).
Если
![]() ,
то
,
то
![]() .
.
Пример 10.5. Пусть
n=10.
Тогда
![]() и
и![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Из теоремы Эйлера непосредственно выводима
Теорема
10.2. (малая
теорема Ферма). Если
![]() ,
то
,
то
![]() .
.
Имеет место следующее утверждение
Теорема
10.3. Если
числа
![]() попарно взаимно простые, число
попарно взаимно простые, число![]() – их произведение,x
и a
– целые числа, то
– их произведение,x
и a
– целые числа, то
![]() .
.
Последнее утверждение является следствием теоремы, которая известна как «китайская теорема об остатках».
Пример 10.6. Пусть
n=10=![]() ;x=81;
a=61.
Тогда
;x=81;
a=61.
Тогда
![]() ,
, ![]() ,
,![]() ,
,
![]() ,
, ![]() ,
,![]() .
.
Шифрование с открытым ключом
Шифрование с открытым ключом производится следующим образом.
Получателем сообщений производится генерация открытого ключа (пара чисел n и e) и закрытого ключа (число d). Для этого:
выбираются два простых числа p и q;
определяется первая часть открытого ключа n=pq;
определяется вторая часть открытого ключа – выбирается небольшое нечетное число e, взаимно простое с числом
 (заметим,
что
(заметим,
что
 );
);определяется закрытый ключ:
 .
.
После чего открытый ключ (числа n и e) сообщается всем отправителям сообщений.
Отправитель шифрует сообщение (разбивая его, если нужно, на слова
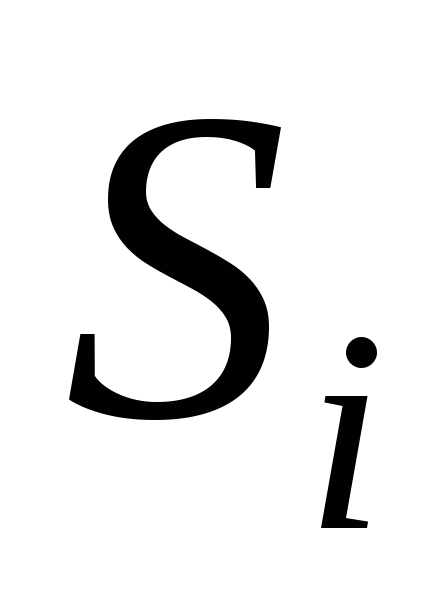 длиной менее
длиной менее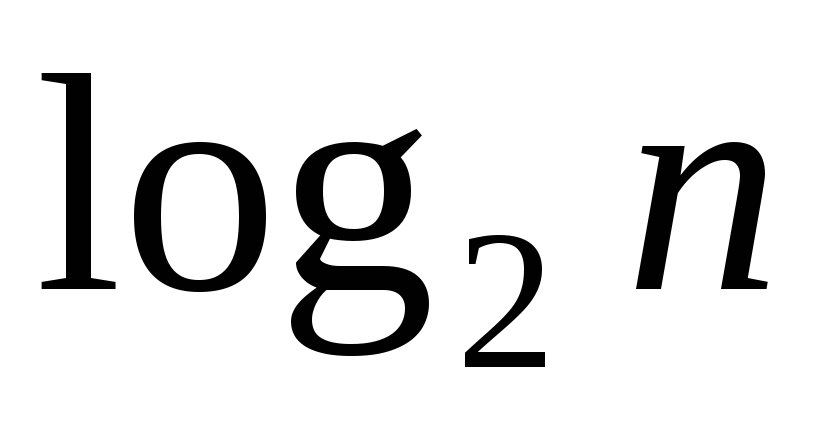 разрядов):
разрядов):
![]() ,
,
и отправляет получателю.
Получатель расшифровывает сообщение с помощью закрытого ключа d:
![]() .
.
Теорема
10.4. Шифрование
с открытым ключом корректно, то есть в
принятых обозначениях
![]() .
.
Доказательство.
Очевидно, что
![]() .
Покажем, что
.
Покажем, что![]() .
Действительно числаd
и e
взаимно обратны по модулю
.
Действительно числаd
и e
взаимно обратны по модулю
![]() ,
то есть
,
то есть
![]()
при некотором k.
Если
![]() ,
то по малой теореме Ферма имеем:
,
то по малой теореме Ферма имеем:
![]() .
.
Если
![]() ,
то сравнение
,
то сравнение![]() ,
очевидно, выполняется. Таким образом,
,
очевидно, выполняется. Таким образом,
![]() .
.
Совершенно аналогично имеем
![]() .
.
И по следствию к китайской теореме об остатках
![]() .
.
Поскольку
![]() и
и![]() ,
заключаем, что
,
заключаем, что![]() .
.
Пример 10.7. Генерация ключей:
p=3, q=11;
n=
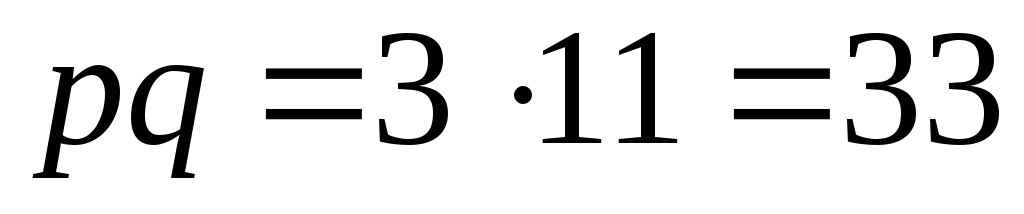 ;
;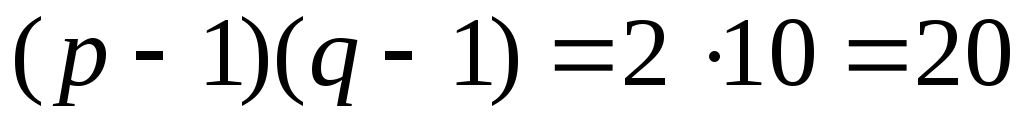 ,
e=7;
,
e=7;d=
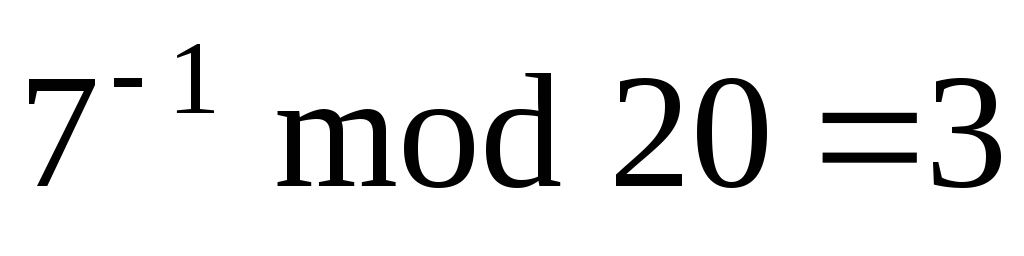 ,
(
,
( ).
).
Пусть
![]() =3,
=3,![]() =1,
=1,![]() =2
(
=2
(![]() ).
Тогда код определяется следующим
образом:
).
Тогда код определяется следующим
образом:
![]() ;
;
![]() ;
;
![]() .
.
При расшифровке имеем:
![]() ,
,
![]() ,
,
![]() .
.
Шифры с открытым ключом сравнительно просты в реализации, очень практичны (поскольку нет необходимости пересылать по каналам связи закрытый ключ и можно безопасно хранить его в одном месте) и в то же время обладают высочайшей криптостойкостью.
Кажется, что дешифровать сообщение несложно: достаточно разложить открыто опубликованное число n на множители, восстановив числа p и q, и далее можно легко вычислить секретный ключ d.
Однако дело заключается в следующем. В настоящее время известны эффективные алгоритмы определения простоты чисел, которые позволяют за несколько минут подобрать пару очень больших простых чисел (по 100 и больше цифр в десятичной записи). В то же время неизвестны эффективные алгоритмы разложения очень больших чисел на множители. Разложение на множители числа в 200 и больше цифр потребовало бы сотен лет работы самого лучшего суперкомпьютера. При практическом применении шифров с открытым ключом используют действительно большие простые числа (не менее 100 цифр в десятичной записи, а обычно – значительно больше). В результате вскрыть этот шифр оказывается невозможно, если не существует эффективных алгоритмов разложения на множители.
Впрочем, возможность открытия таких алгоритмов существует, хотя этот факт и не доказан строго.
