X(баскетболист(X)высокий(X))

«Два плюс три равно пяти».

равно(плюс(два, три), пять)

«Некоторые люди любят грибы»

X(личность(х)любит(х, грибы))

«Никто не любит платить налоги»

X любит(х, платить(налоги))

7. Правила логического вывода

Возможность логически выводить новые правильные выражения из набора истинных утверждений – это важное свойство исчисления предикатов. Логически выведенные выражения корректны, потому что они совместимы со всеми предыдущими интерпретациями первоначального набора выражений.

Одним из наиболее важных правил логического вывода является «MODUS PONENS» (переводится с латинского как «правило отделения»). Другие полезные правила вывода называются «MODUS TOLLENS» («правило исключения»), «Транзитивность», «Слияние», «Исключение «И»», «Введение «И»», «Универсальное инстанцирование».

• Если известно, что предложения A и AB истинны, то модус поненс позволяет вывести истинность B. Формально это записывается следующим образом: .

• Согласно правилу вывода модус толленс, если известно, что AB является истинным и B ложно, то можно вывести истинность A. Формально: .

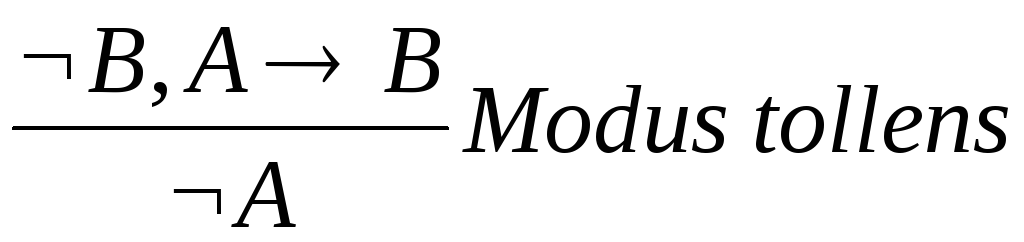• Транзитивность – если известно, что выражения AB и ВС истинны, то истинно и выражениеAС. Формально:.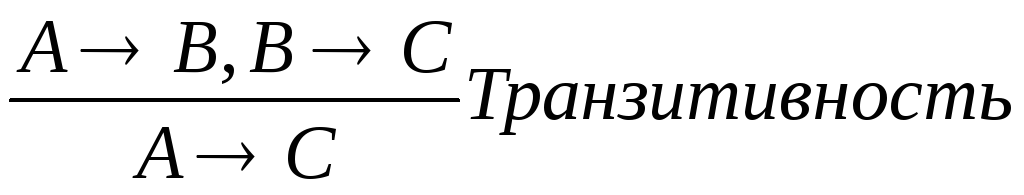

• Слияние – если известно, что выражения AB и АВ истинны, то истинно и выражениеB. Формально: .

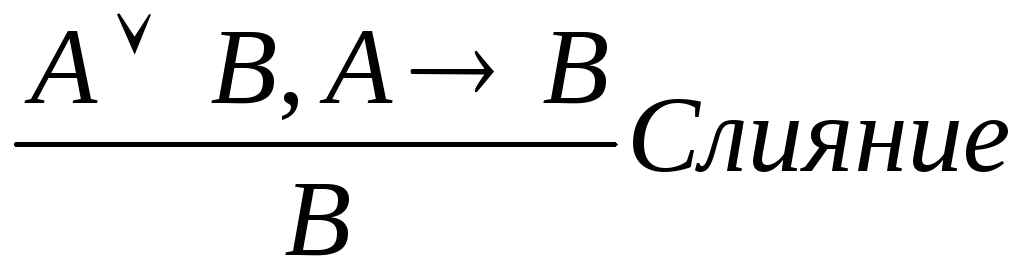• Исключение «И» – правило, позволяющее вывести истинность обоих конъюнктов на основе истинности конъюнктивного предложения. Например, если AB истинно, можно сделать вывод, что A и B истинны. Формально: .

• Введение «И» – позволяет вывести истинность конъюнкции из истинности ее конъюнктов. Например, если A и B истинны, то конъюнкция AB также истинна. Формально: .

• Универсальное инстанцированние сводится к следующему: если любую переменную, стоящую под квантором всеобщности в истинном предложении, заменить любым соответствующем термом из области определения, то результирующее выражение истинно. Таким образом, если «a» принадлежит той же области определения, что и Х и Xр(Х), то можно вывести истинность р(а).

Пример 4.7. Рассмотрим предложения: P «идет дождь» и PQ «если идет дождь, то земля будет влажной». Согласно правилу модус поненс предложение Q «земля является влажной» является истинным, если истинны предложения P и PQ.

Пример 4.8. Правило модус поненс может быть также применено к выражениям, содержащим переменные. Рассмотрим в качестве примера известный силлогизм: «Все люди смертны, и Сократ – человек, поэтому Сократ – смертен».

«Все люди смертны» и «Сократ – человек» может быть представлено в исчислении предикатов следующим образом:

X(человек(X)смертный(X)),

человек(сократ).

Поскольку Х в выражении стоит под знаком квантора всеобщности, его можно заменить любым значением из области определения Х, и при этом утверждение будет сохранять истинное значение согласно правилу универсального инстанцирования. Заменив в выражении Х на «сократ», получим следующее утверждение

человек(сократ)смертный(сократ).

Применив правило модус поненс, приходим к выводу: смертный(сократ).

8. Правило резолюции

Правило резолюции (лат. resolutio – решение ): если выражения PAC и QBC являются истинными, то выражение AВ тоже истинно. Формально можем записать:

.

Предложения PAC и QBC называются резольвируемыми (или родительскими), предложение AВ – резольвентой, а формулы С и С – контрарными литералами.

Правило резолюции является более общим правилом логического вывода по сравнению с рассмотренными ранее. Модус поненс и многие другие правила вывода являются частными случаями правила резолюции.

Для доказательства справедливости правила резолюции рассмотрим табл. 4.6.

Таблица 4.6

№	A	B	C	PAC	QBC
0	0	0	0	0	1	0	0
1	0	0	1	1	0	0	0
2	0	1	0	0	1	0	1
3	0	1	1	1	1	1	1
4	1	0	0	1	1	1	1
5	1	0	1	1	0	0	1
6	1	1	0	1	1	1	1
7	1	1	1	1	1	1	1

Как можно видеть, значения функций исовпадают в выделенных серым цветом строках. Этого вполне достаточно для того, чтобы правило резолюции являлось справедливым.

Принцип резолюции описывает способ обнаружения противоречий в базе данных дизъюнктивных выражений. В его основе лежит идея «доказательства от противного». Процесс доказательства состоит из следующих этапов.

1. Исходные аксиомы приводятся к дизъюнктивной форме.

2. К набору аксиом добавляется отрицание доказываемого утверждения в дизъюнктивной форме.

3. Выполняется совместное разрешение этих дизъюнктов, в результате чего получаются новые основанные на них дизъюнктивные выражения.

4. Генерируется пустое выражение, означающее противоречие.

5. Подстановки, использованные для получения пустого выражения, свидетельствуют о том, что отрицание отрицания – истинно.

Пример 4.9. Докажем, что утверждение «Мухтар смертен» следует из утверждений «Мухтар – собака», «Собаки – это животные» и «Все животные смертны». Преобразовывая эти аксиомы в предикатную форму и применяя правило модус поненс, получим следующее.

1. Собаки – это животные: Х(собака(Х)животное(Х)).

2. Мухтар – собака: собака(мухтар).

3. На основе модус поненс и подстановки (мухтар/Х) получим: животное(мухтар).

4. Все животные смертны: Y(животное(Y)умрет(Y)).

5. На основе модус поненс и подстановки (мухтар/Y) получим: умрет(мухтар).

По принципу резолюции эти предикаты необходимо преобразовать в дизъюнктивную форму.

Предикатная форма	Дизъюнктивная форма
Х(собака(Х)животное(Х))	собака(Х)животное(Х)
собака(мухтар)	собака(мухтар)
Y(животное(Y)умрет(Y))	животное(Y)умрет(Y)

Полученную базу данных можно записать в виде конъюнктивной нормальной формы (КНФ) – т.е. в виде конъюнкции дизъюнктов.

(собака(Х)животное(Х))(животное(Y)умрет(Y))(собака(мухтар)).

К этому выражению с помощью конъюнкцию следует добавить отрицание целевого выражения, в данном случае умрет(мухтар). Выполняя резолюцию, получим новые дизъюнктивные выражения, представленные на рис. 4.2.

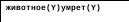
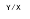
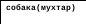
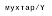
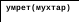
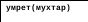
Рис. 4.2. Доказательство утверждения «Мухтар смертен» методом резолюции

Пустой квадрат в нижней части рисунка означает противоречие. При использовании принципа резолюции возможны три случая.

1. Среди текущего множества предложений нет резольвируемых. Это означает, что теорема опровергнута.

2. В результате очередного применения правила резолюции получено пустое предложение. Это означает, что теорема доказана.

3. Процесс не заканчивается, то есть множество предложений пополняется все новыми резольвентами, среди которых нет пустых. Это ничего не означает.