
- •Конспект лекций по дисциплине «основы дискретной математики»
- •Лекция № 1. Дискретное и непрерывное
- •Лекция № 2. Системы счисления
- •Лекция № 3. Фракталы
- •3.1. Канторово множество
- •3.2. Ковер Серпинского и снежинка Коха
- •3.3. Стохастические фракталы
- •3.4. Энтропийная размерность
- •3.5. Фрактал Мандельброта
- •Лекция № 4. Основы математической логики
- •Набор истинностных значений 0001 в первой строке таблицы соответствует результатам операций:
- •Основные эквивалентности:
- •X(баскетболист(X)высокий(X))
- •X(личность(х)любит(х, грибы))
- •X любит(х, платить(налоги))
- •X(человек(X)смертный(X)),
- •Лекция № 5. Множества и подмножества
- •Лекция № 6. Математическая индукция
- •Лекция № 7. Комбинаторика
- •Лекция № 8. Числа фибоначчи и простые числа
- •Лекция № 9. Кодирование
- •Лекция № 10. Шифрование
3.3. Стохастические фракталы
Стохастические фракталы получаются в том случае, если в итерационном процессе случайным образом менять какие-либо параметры. При этом получаются объекты, очень похожие на природные – несимметричные деревья, поверхности скал, изрезанные береговые линии. В принципе, снежинка Коха очень похожа на природный объект (обычную снежинку), хотя это не стохастический фрактал.
В 1977 году в свет вышла книга американского математика Бенойта Мандельброта (1924-2010) «Фрактальная геометрия природы», в которой этот ученый привлек внимание широкой общественности к потрясающей красоте мира фракталов.
Графики случайных процессов, которые можно наблюдать на дисплеях приборов или на лентах самописцев, также является фракталами. Такие графики академик Яков Борисович Зельдович (1914-1987), полушутя, называл «толстой линией». В своей работе (Зельдович Я.Б., Соколов Д.Д. Фракталы, подобие, промежуточная асимптотика// Успехи физических наук, Том 146, вып. 3, июль 1985. – 493-574.) Зельдович привел пример модели такой линии
![]() , (3.1)
, (3.1)
где
![]() – последовательность независимых
случайных чисел, равномерно распределенных
между 0 и
– последовательность независимых
случайных чисел, равномерно распределенных
между 0 и![]() (случайный параметр). Ряд (3.1) сходится
при
(случайный параметр). Ряд (3.1) сходится
при![]() .
Однако обычной производной у функции
.
Однако обычной производной у функции![]() в этом случае нет, поскольку соответствующий
ряд
в этом случае нет, поскольку соответствующий
ряд![]() расходится при
расходится при![]() .
Таким образом, очевидно, что к функциям
с не слишком быстро убывающим спектром
идеи анализа применимы не в полной мере.
.
Таким образом, очевидно, что к функциям
с не слишком быстро убывающим спектром
идеи анализа применимы не в полной мере.
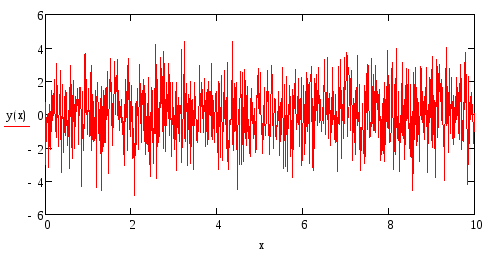
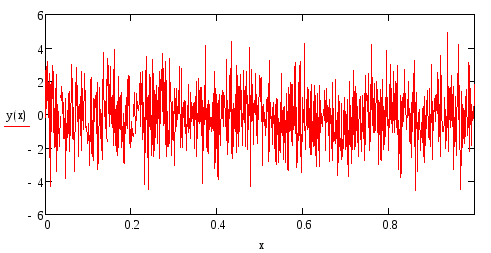
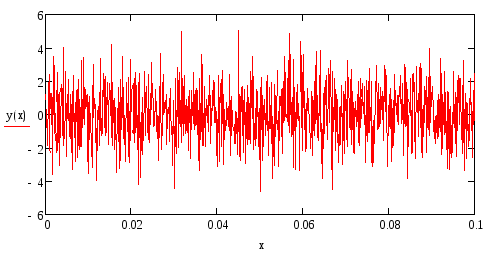
Рис. 3.5. Стохастический фрактал в различных масштабах
На рис. 3.5 показаны
графики функции
![]() ,
построенные вMathCAD
для различных интервалов изменения
аргумента. При построении графиков
использовался алгоритм
,
построенные вMathCAD
для различных интервалов изменения
аргумента. При построении графиков
использовался алгоритм
![]() ,
,
где
![]() – функция, генерирующая случайные
числа, равномерно распределенные в
диапазоне от 0 до 1. Как можно видеть,
фрактальная кривая единообразно устроена
в широком диапазоне масштабов.
– функция, генерирующая случайные
числа, равномерно распределенные в
диапазоне от 0 до 1. Как можно видеть,
фрактальная кривая единообразно устроена
в широком диапазоне масштабов.
3.4. Энтропийная размерность
Пусть X
– компактное пространство с метрикой
d.
Тогда множество
![]() называетсяr-плотным,
если
называетсяr-плотным,
если
![]() ,
где
,
где![]() – шар радиусаr
относительно метрики d
с центром в точке x.
Определим r-емкость
пространства (X,
d)
как минимальное число элементов
– шар радиусаr
относительно метрики d
с центром в точке x.
Определим r-емкость
пространства (X,
d)
как минимальное число элементов
![]() в егоr-плотном
множестве.
в егоr-плотном
множестве.
Пример 3.1.
Например, если X
– это отрезок [0, 1] с обычной метрикой,
то значение
![]() приближенно равно 1/(2r),
потому что необходимо 1/(2r)
шаров (т.е. интервалов), чтобы покрыть
единичный отрезок.
приближенно равно 1/(2r),
потому что необходимо 1/(2r)
шаров (т.е. интервалов), чтобы покрыть
единичный отрезок.
Пример 3.2.
Возьмем единичный квадрат
![]() .
Тогда значение
.
Тогда значение![]() имеет порядок
имеет порядок![]() ,
потому что требуется по крайней мере
,
потому что требуется по крайней мере![]() шаров радиусаr,
чтобы покрыть единичный квадрат.
Аналогично, для единичного куба значение
шаров радиусаr,
чтобы покрыть единичный квадрат.
Аналогично, для единичного куба значение
![]() имеет порядок
имеет порядок![]() .
.
Определение.
Если X
– вполне
ограниченное метрическое пространство,
тогда число
![]() называется
энтропийной размерностью пространства
X
.
называется
энтропийной размерностью пространства
X
.
В англоязычной литературе для энтропийной размерности используют термин «box dimension».
Пример 3.3.
Если
![]() ,
то
,
то![]() .
.
Если
![]() ,
то
,
то![]() .
.
Если
![]() ,
то
,
то
![]() .
.
Пример 3.4. Найдем энтропийную размерность для менее тривиальных пространств.
Троичное канторово множество. Если С – троичное канторово множество, то
 (см. табл. 3.1) и
(см. табл. 3.1) и
![]() .
.
В табл. 3.1, приведены данные, помогающие понять логику вычисления размерности троичного канторова множества.
Таблица 3.1
|
|
i |
r |
|
|
0 |
1 |
1 | |
|
1 |
1/3 |
| |
|
2 |
|
| |
|
3 |
|
|
Ковер Серпинского. Для квадратного ковра Серпинского S
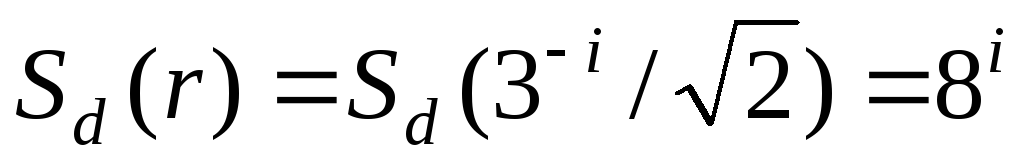 и
и
 .
.
Для треугольного
ковра Серпинского подобным способом
получаем, что его энтропийная размерность
равна
![]() .
.
Снежинка Коха. Для снежинки Коха К мы имеем
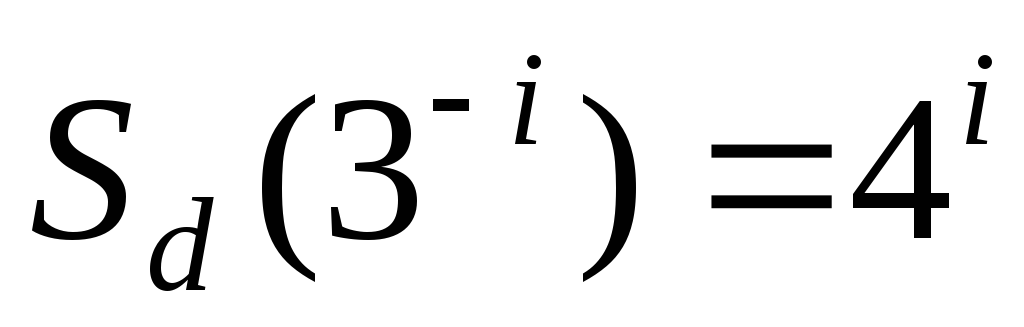 ,
так как ее можно покрыть шарами с
центрами на ребрахi-го
многоугольника. Таким образом,
,
так как ее можно покрыть шарами с
центрами на ребрахi-го
многоугольника. Таким образом,
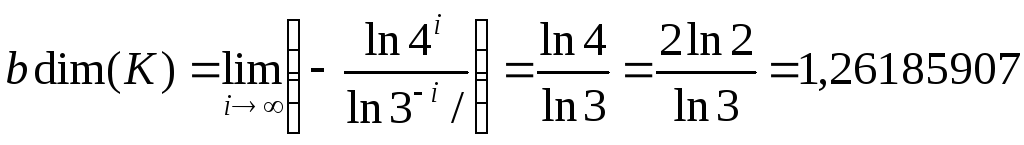 .
.

