Лекция № 7. Комбинаторика

1. Введение

Во многих практических случаях возникает необходимость подсчитать количество возможных комбинаций объектов, удовлетворяющих определенным условиям. Такие задачи называются комбинаторными. Раздел математики, который их изучает, называется комбинаторикой.

Одними из наиболее важных понятий комбинаторики являются размещения и сочетания.

Способ расположения в определенном порядке некоторого числа элементов из заданного множества, когда существенна последовательность выбора элементов, называется размещением. Если же последовательность выбора элементов несущественна, то способ выбора называется сочетанием.

Пример 7.1. Дано множество S, состоящее из трех элементов: a, b, c. Необходимо определить количество комбинаций по два элемента из представленных трех.

1. Повторение элементов не допускается:

а) существует 6 размещений (ab, ac, ba, bc, ca, cb);

б) существует 3 сочетания (ab, bc, ca).

2. Повторение элементов разрешается:

а) существует 9 размещений (aa, ab, ac, ba, bb, bc, ca, cb, cc);

б) существует 6 сочетаний (aa, ab, ac, bb, bc, cc).

2. Размещения без повторений

Общее число размещений без повторений из n элементов по k элементов обычно обозначается так: .

Теорема 7.1.

. (7.1)

Доказательство. Задача сводится к заполнению k пустых мест символами элементов (рис. 7.1).

Рис. 7.1.

Первое место можно заполнить n различными способами, поскольку имеется n элементов, и повторения не допускаются. Второе место n – 1 способами, поскольку один элемент уже задействован. Третье место n – 2 способами, поскольку два элемента уже задействованы и т. д. Последнее k-тое место можно заполнить различными способами. Общее количество размещений будет равно произведению способов заполнения каждого изk мест.

Следствие. При n = k

Размещение (приn = k) называется перестановкой.

Пример 7.2. Если дано множество, состоящее из трех элементов: a, b и c, то количество размещений по два элемента равно , что соответствует результату, приведенному в примере 7.1.

3. Сочетания без повторений

Число различных сочетаний без повторений обычно обозначается так: . Или так.

Теорема 7.2. (7.2)

Доказательство. Очевидно, что , поскольку одному сочетанию элементов соответствует несколько размещений, а именно:.

С учетом формулы (7.1) формулу (7.2) можно записать следующим образом:

. (7.3)

Таким образом, сочетания без повторений и биномиальные коэффициентыявляются равнозначными понятиями.

Пример 7.3. Если дано множество, состоящее из трех элементов: a, b и c, то количество сочетаний по два элемента равно: . Это соответствует результату, приведенному в примере 7.1.

4. Размещения с повторением

Если мы выбираем из множества n элементов размещения с повторениями k элементов, то в данном случае k может превосходить n.

Теорема 7.3. Общее число размещений с повторениями k элементов, взятых из совокупности n различных элементов, равно .Доказательство. Задача сводится к заполнению k пустых мест символами n элементов. Каждое место можно заполнить n различными способами, поскольку повторения допускаются. Общее количество размещений будет равно произведению способов заполнения каждого из k пустых мест, то есть: .

Пример 7.4. Максимальное число знаков, которые могут быть представлены с помощью k двоичных символов (k бит), равно числу размещений с повторением из множества, содержащего всего два элемента 0 или 1. Например, если k = 8 (один байт), то =256.

Пример 7.5. Код Бодо (Жан Морис Эмиль Бодо (1845-1903) – французский изобретатель в области телеграфии) использует для кодирования два элементарных сигнала – импульс и паузу, при этом сопоставляемые буквам кодовые слова состоят из пяти таких сигналов. Значит, код Бодо способен передавать = 32 букв. Латинский алфавит содержит 26 букв. С помощью кода Бодо можно также передавать шесть дополнительных знаков, например: знак пропуска между словами, точку, запятую, вопросительный знак, восклицательный знак и двоеточие.

Пример 7.6. Часто по разным соображениям (например, по соображениям безопасности и помехозащищенности) для кодирования сообщений используют не все возможные последовательности в данном алфавите, а только некоторые из них, удовлетворяющие тем или иным ограничениям. Рассмотрим двоичные слова, состоящие из k букв, причем все они имеют фиксированное число t единиц (или, как говорят, слова постоянного веса t). Подсчитаем общее количество таких слов. Каждое из них получится, если мы выберем некоторым образом t позиций из k, и запишем в них единицы, а в остальных k – t позициях – нули. Значит, число всех слов постоянного веса совпадает с числом сочетаний из k элементов по t, т.е. равно

. (7.4)

5. Сочетания с повторением

Теорема 7.4. Общее число сочетаний с повторениями k элементов, взятых из совокупности n различных элементов, равно

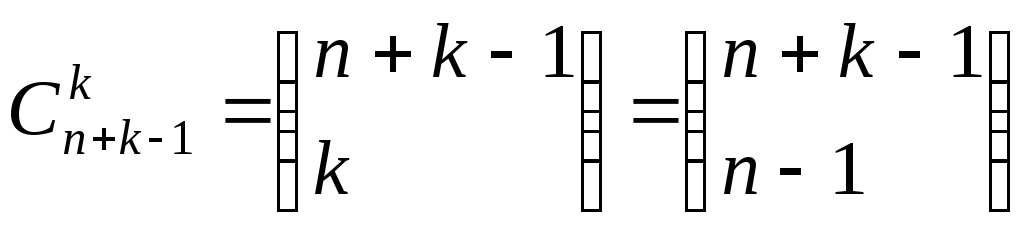. (7.5)

Доказательство. Сведем задачу к случаю сочетаний без повторений. Для этого каждый повторяющийся элемент условно будем считать новым элементом, который прибавляется к исходному множеству из n элементов. Среди k элементов в сочетании хотя бы один обязательно должен принадлежать исходному множеству из n элементов. Иначе, мы смогли бы построить сочетание, не включающее в себя ни одного элемента из исходного множества n элементов. А это противоречит условию задачи.

Поэтому количество добавленных элементов не может быть равно k (или превосходить это число). Однако легко построить сочетание, в котором будет (и меньше) повторяющихся (и значит условно новых) элементов.

Таким образом, сведя задачу к случаю сочетания без повторений, мы теперь имеем n «старых» и «новых» (повторяющихся) элементов. Всего:. Далее обращаемся к формуле (7.3), описывающей число сочетаний без повторений, и, подставляявместо, получаем формулу (7.5).

Пример 7.7. Найти число сочетаний из 5 различных элементов по 3.

1. Если повторение элементов не разрешено: .

2. Если повторение элементов разрешено: .

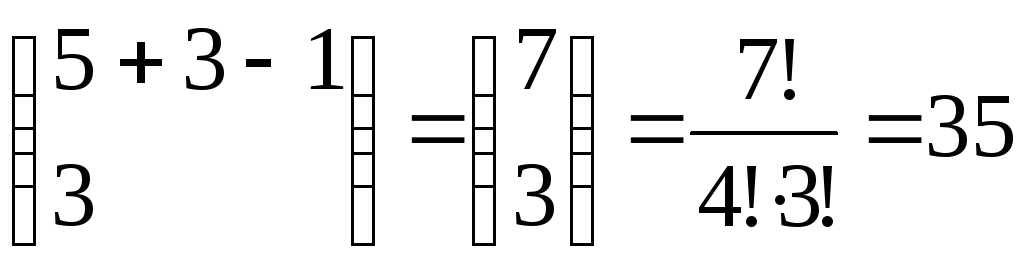6. Формула Стирлинга

Рассматривая комбинаторные задачи, мы часто сталкиваемся с факториалами. Факториал – это очень быстро растущая функция, она растет быстрее экспоненты. При достаточно больших n (n > 10) для определения факториала n! Можно использовать приближенную формулу Стирлинга:

. (7.6)

Погрешность такого приближения определяется формулой

. (7.7)

Нетрудно показать, что .

7. Подстановки

Взаимно однозначная функция называетсяподстановкой на . Если множествоконечно (), то можно считать, что. В этом случае подстановкуудобно задавать таблицей из двух строк. В первой строке – значения аргументов, во второй – соответствующее значение функции. Ниже приведены примеры произвольных дискретных подстановоки:

, .

Произведением подстановок иназывается их суперпозиция.Суперпозиция – это результат последовательного применения двух подстановок. Произведение двух приведенных выше подстановок равно

.

Для вычисления результата был использован следующий алгоритм. Первый по номеру элемент подстановки равен 5. Поэтому обращаемся к пятому по номеру элементу подстановкии видим, что он также равен 5. Значит, первый элемент произведениябудет равен 5.

Второй элемент равен 2. Поэтому обращаемся ко второму элементуи видим, что он равен 1. Последнее значение принимаем в качестве второго элемента произведения. Действуя аналогичным образом, получаем все оставшиеся элементы произведения.

Как можно видеть произведение подстановок также является подстановкой. Произведение подстановок определено для подстановок одинакового размера. Произведение подстановок в общем случае не обладает свойством коммутативности, то есть

.

Единичная (или тождественная) подстановка – это подстановка такая, что. Например:

.

Обратная подстановка по отношению к подстановке– это подстановка, удовлетворяющая соотношению:

. (7.8)

Таблицу обратной подстановки можно получить, если просто поменять местами строки таблицы исходной подстановки. Например:

, .

Подстановки можно представлять в графической форме, проводя стрелки от каждого элемента к элементу.

Пример 7.8. Задана постановка

.

Графическое представление этой подстановки показано на рис. 7.2.

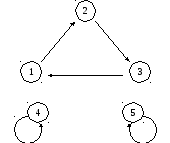
Рис. 7.2

В современной математике алгебраические операции применяют не только к скалярным числам, но и к другим объектам. Например, к матрицам или подстановкам. Множества различных объектов, для которых определены соответствующие алгебраические операции, называются алгебрами в широком смысле этого слова. Если определены четыре действия: сложение, вычитание, умножение и деление – такая алгебра называется полем.

Таким образом, обычная алгебра (в узком смысле этого слова) является полем. Если операция деления в алгебре не определена, такая алгебра называется кольцом. Если определена только одна операция, то алгебра называется группой. Причем, эта операция должна обладать свойством ассоциативности:

,

сама алгебра должна иметь единичный элемент со свойством:

,

и для каждого объекта иметь обратный элемент:

.

Теперь мы можем утверждать, что множество подстановок образуют группу относительно операции суперпозиции. Эта группа называется симметрической степени n.

Цикл – это последовательность элементов , такая что

Цикл длины 2 называется транспозицией.

Если принять соглашение, что элементы верхней строки (аргументы) всегда располагаются в определенном порядке (например, по возрастанию), то верхнюю строку можно не указывать – подстановка однозначно определяется нижней строкой. Такие подстановки в одну строку называются перестановками. Перестановку элементов будем обозначать, где все– различные числа из диапазона.

Если в перестановке для элементовиимеет место неравенствопри, то параназываетсяинверсией. Обозначим –число инверсий в перестановке .

Теорема 7.5. Произвольную подстановку можно представить в виде суперпозициитранспозиций соседних элементов.

Доказательство. Пусть . Переставим 1 на первое место, меняя ее местами с соседними слева элементами. Обозначим последовательность этих транспозиций через. При этом все инверсии, в которых участвовала 1, пропадут. Затем переставим 2 на второе место и т.д. Таким образом,и по свойству группы, причем.

Следствие. Всякая сортировка может быть выполнена перестановкой соседних элементов.

Такой метод сортировки известен как пузырьковый метод. Этот метод прост, но является далеко не самым эффективным алгоритмом сортировки.