(z)		можно	вычислить			выбо-
k	n−1			рочное	значение		статисти-
					)
				ки zв = DX (n −1) D0					и
		α		сравнить ее с критической
				точкой	zпр,1−α .			Если
				zв ≥ zпр,1−α , гипотезу					H0
W \ ω			ω z	следует отклонить, если же
		z	−	zв < zпр,1−α ,		гипотеза			H0
		пр,1	α	принимается		с	уровнем
Рис. 5.8. Правосторонняя критическая область для				значимости α.
дисперсии

5.4.Проверка гипотез о параметрах двух нормальных распределений

1.Проверка гипотезы о равенстве математических ожиданий двух нормальных распределений с известными дисперсиями.

Проверка гипотезы о равенстве математических ожиданий двух нормальных совокупностей имеет важное практическое значение. Часто возникает вопрос, можно ли отличие двух средних, полученных по двум разным выборкам, объяснить случайной ошибкой экспериментов или оно не случайно? Подобная задача возникает, например, при сравнении качества изделий, изготовленных на разных установках.

Пусть x1, x2

,..., xn - первая выборка,

y1, y2 ,..., yn

- вторая выборка и

xi N(mX , DX ),

1

2

y j N(mY , DY ), причем

DX

и

DY

должны быть из-

вестны.

Основная проверяемая

гипотеза

в этих

условиях

имеет

вид

H0 : mX = mY .

1

n1

Вычислим

оценки

математических

ожиданий

mX

=

∑xi

и

n

1 i=1

m

=

1

n2 y

i

.

Очевидно,

что

m

N(m

X

, D

X

n ),

а

Y

∑

X

1

n2 i=1

m

N

(m , D

n

2

). Тогда из свойств матожидания и дисперсии незави-

Y

Y

Y

M (mX − mY )=

симых

случайных

величин

следует,

что

= M (mX )− M (mY )= mX − mY ,

а

D(mX − mY )= D(mX )+ D(mY )=

= DX n1 + DY n2 .

118

Таким образом, в силу теоремы о суммировании нормально распре-

деленных

случайных

величин

будем

иметь

m

− m

N(m

X

− m , D

X

n + D

n

2

). Тогда

нормированная

и цен-

X

Y

Y

1

Y

трированная случайная величина будет подчинена стандартному нормаль-

ному распределению, т.е.			z = (mX − mY )− (mX − mY ) N(0,1)			. Эту ста-
			DX n1 + DY n2
тистику	и выбирают за		рабочую	при	проверке нулевой	гипотезы
H0 : mX	= mY . Если H0 выполняется, то				mX −mY = 0 и рабочая стати-
стика упрощается z =		(mX − mY )		N(0,1).
		DX	n1 + DY
				n2

Дальнейшие действия стандартны и практически совпадают с аналогичными действиями при проверке гипотезы о равенстве матожидания выборки определенному значению при известной дисперсии (см. под-

	разд. 5.3, п.1). Задаем			α и строим левостороннюю критическую область
	(− ∞, zлев,α) = (− ∞,tα), где tα				-
	α-процентный квантиль стан-						f (z H0 )
	дартного нормального распре-
	деления. Затем находим выбо-
	рочную		статистику			α
		(mX − mY )
	zв =			. Если
		DX n1 + DY	n2
	zв < tα , гипотеза		H0	должна		ω	W \ ω
	быть отвергнута (рис. 5.9). В					tα
	случае правостороннего				и	Рис. 5.9. Левосторонняя критическая область
	двустороннего критериев вы-					статистики z при H 0 : mX		= mY
	полняется комплекс аналогич-
	ных действий.
		2. Проверка	гипотезы		о	равенстве	математических	ожиданий

двух нормальных распределений с неизвестными, но равными дисперсиями.

Пусть	имеются две случайные	величины X N(mX , D) и
Y N(mY , D)	с одинаковыми дисперсиями	D , однако числовое значение

Dнеизвестно, неизвестны также и числовые значения матожиданий mX

иmY . Пусть имеются две выборки этих случайных величин x1, x2,..., xn1 и

119

y1, y2 ,..., yn2 . Тогда mX N(mX , Dn1 ), mY N(mY , Dn2 ), кроме того

)

(n −1)

D

χ2

и

)

(n

−1)

D χ2

.

D

X

D

X

2

1

n1 −1

n2 −1

неза-

Наблюдения организованы так, что результаты и y1, y2 ,..., yn2

висимы. Из этого условия следует, что mX

)

)

и mY независимы, DX

и DY

также независимы. Требуется проверить гипотезу H1 : mX

> mY .

Подберем подходящую статистику для этого критерия. По предыду-

щему пункту, очевидно,

(mX − mY )− (mX − mY ) N(0,1) . Кроме того, по

D n1 + D n2

свойству χ2 -распределения имеем:

если

DX (n1 −1)

χn2

−1

и

DY (n2 −1)

χn2

−1 ,

то

D

1

D

2

DX (n1 −1)

+

DY (n2 −1)

χ

2

.

D

D

n2 +n2 −2

Вспомним способ получения статистики распределения Стьюдента

(см. подразд. 2.2): t = z

n

v , где

z N(0,1), а v χn2 . В нашем случае

z = (mX − mY )− (mX − mY )

, а

vn

+n

2

−2 =

DX (n1 −1)

+

DY (n2 −1)

.

Тогда

D n1 + D n2

1

D

D

(mX − mY )− (mX − mY )

n

+ n

2

−

2

D n

+ D n

1

tn

−2 =

+n

2

)

1

2

)

=

1

DX

(n1 −1)+ DY (n2 −1)

(mX

D

=

− mY )− (mX − mY )

.

Если

гипотеза

H0 : mX

= mY

)

)

(n2 −1)

(1 n +1 n

2

)

DX (n1

−1)+ DY

1

n1 + n2 − 2

выполняется,

то

mX −mY = 0

и

вид

статистики

упрощается

tn

+n

−2 =

(mX − mY )

)

.

2

)

1

(1 n +1 n

)

DX (n1 −1)+ DY (n2 −1)

2

1

n1 + n2 − 2

120

Итак, рабочая статистика получена. Зададим уровень значимости α и перейдем к построению критической области. Выберем правосторонний

критерий, т.е. альтернативная

гипотеза

будет

иметь

вид

H1 : mX

> mY . Правосторон-

sn

−2 (t)

няя

критическая

область

со-

+n

2

стоит

из

интервала

1

(zпр,1−α,+∞)= (t1−α,n +n

2

−2,+∞),

1

где

t1−α,n1+n2 −2

-

(1 − α) -

α

процентный

квантиль

рас-

пределения

Стьюдента

(рис. 5.10). Он определя-

ется

из

условия

P(z > zпр,1−α = t1−α,n +n

2

−2 )= α

W \ ω

t1−α,n +n

−2

ω

1

2

+∞

1

или

∫s(t)dt = α ,

т.е.

Рис. 5.10. Правосторонняя критическая область

t1−

α,n

+n

2

−2

статистики z при H 0 : mX

= mY

1

t

−n

−2

= S −1(1 − α).

Если

выборочная

статистика

1−α,n

2

1

(mX − mY )

1 n1

zв

=

)

(n

)

−1)

,

где

mX

=

∑xi ,

(1 n +1 n

)

D

X

−1)+ D (n

2

n1 i=1

2

1

Y

1

n1 + n2

− 2

1

n2

)

1

n1

2

)

1

n2

2

mY =

∑ yi , DX

=

∑

(xi − mX )

,

DY =

∑(yi

− mY )

не

n

n −1

n

−1

2 i =1

1

i=1

2

i =1

превысит

t1−α,n

+n

2

−2 , то гипотезу

H0

следует принять с уровнем зна-

1

чимости α.

3. Проверка гипотезы о равенстве дисперсий двух нормальных распределений.

Задача проверки гипотезы о равенстве дисперсий часто возникает на практике. Дисперсия характеризует точность работы приборов. Убедившись в равенстве двух дисперсий, можно быть уверенным, например, что два прибора, два технологических процесса обеспечивают одинаковую точность.

Пусть x1, x2 ,..., xn1 - результаты независимых наблюдений случайной величины X , а y1, y2 ,..., yn2 - случайной величины Y . Все наблюдения проводятся в одинаковых условиях и организованы так, что результаты

121

обеих выборок независимы. При этих условиях требуется проверить нулевую гипотезу H0 : DX = DY .

Построим критерий для проверки этой гипотезы. Пусть

1

n1

1

n2

)

1

n1

2

mX =

∑xi ,

mY =

∑ yi ,

DX =

∑

(xi

− mX ) ,

n

n

n

−

1

1 i =1

2 i =1

1

i =1

)

1

n2

2

DY =

∑(yi

− mY )

- несмещенные оценки матожиданий и диспер-

n2

−1 i =1

X и Y по используемым выборкам.

В под-

сий случайных величин

разд. 5.3 уже использовалась статистика v =

D(n −1)

χn2−1 .

D

В соответствии с определением

F -распределения (см. подразд. 2.3)

отношение (χl2

l)

(χk2

k) имеет F -

распределение с

l

и

k

степенями

fF (n −1,n

−1)

свободы.

В

нашем

случае

дробь

1 2

)

−1)

DX (n1

n1 −1

)

DX

DX

=

DX

будет

)

(n2

1)

)

DY

DY

−

n2 −1

DY

DY

α 2

α 2

иметь F -распределение с

n1 −1 и

n2 −1

степенями

свободы.

Если

zлев,α 2

гипотеза H0 верна,

то DX

= DY

и

для статистики

z справедливо со-

отношение z =

)

)

−1 .

DX

DY Fn −1,n

2

ω

W \ ω

zпр,α 2

ω

1

Рассмотрим

при

заданном

α

дву-

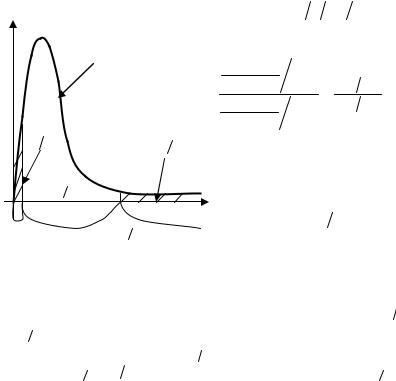
Рис. 5.11. Двусторонняя критическая область

сторонний

критерий,

т.е.

для проверки гипотезы о равенстве дисперсий

H1 : DX

≠ DY

(рис. 5.11).

В

этом

двух нормальных распределений

случае критическая область состоит

из

двух

интервалов

(0, zлев,α 2 )

и

(zпр,α 2 ,+∞), где критические точки находятся по следующим схемам:

P(0 < z < zлев,α 2 )= α 2 ,	zлев,α 2	fF (x)dx =	α		P(z > zпр,α 2 )=	α
	∫			,			,
	0		2			2

122