1.3. Кручение бруса

Кручением называется такой вид деформации, при котором в поперечных сечениях стержня возникает только крутящий момент Мê, остальные внутренние силовые факторы равны нулю. При кручении строят эпюру крутящего момента — ЭМê.

При построении эпюры используют метод сечений. При этом следует иметь в виду следующие закономерности:

—в сечении, где действует внешний сосредоточенный момент, на эпюре крутящего момента происходит скачок на величину внешнего момента;

—на участке стержня между сосредоточенными внешними моментами крутящий момент не изменяется;

—на участке, где действует равномерно распределенный внешний момент, крутящий момент изменяется по линейному закону.

Пример 2

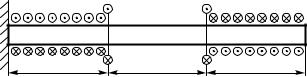
Для стержня, показанного на рисунке 1.4, нагруженного сосредоточенными и равномерно распределенными моментами, построить эпюру крутящего момента (в долях M). Размеры уча- стков стержня и величины действующих сосредоточенных и равномерно распределенных моментов приведены в таблице 1.3.

M1/l	M2	M3	M4/l
l		l1	l2
	Рисунок 1.4

					Таблица 1.3
l1	l2	M1	M2	M3		M4
l	2l	–M	–M	–3M		–2M

17

Решение
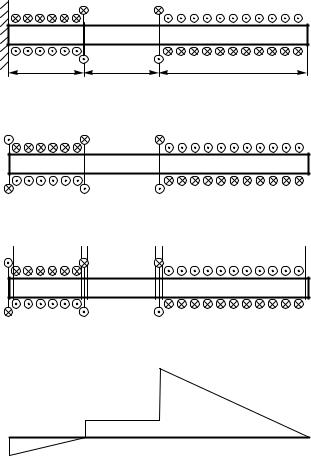
1. Изображаем реальную схему задачи с учетом длин уча-
стков стержня, величин и направлений действующих моментов
в соответствии с данными таблицы 1.3 (рисунок 1.5, а).
	M/l	M	3M		2M/l
	l	l			2l
			à
MêÀ	M/l	M	3M		2M/l
À
			á
	I	II III	IV	V	VI
M	M/l	M	3M		2M/l

â

4M

M

ÝMê

M

ã

Рисунок 1.5

18

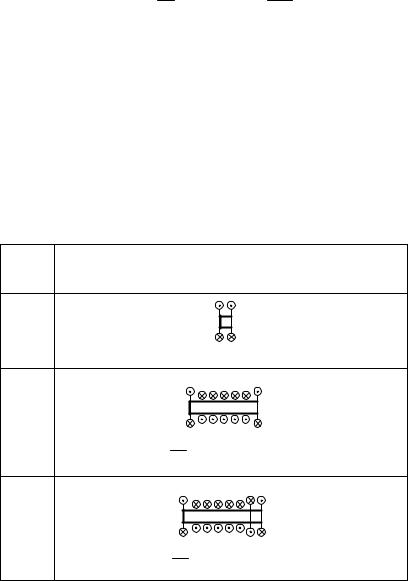
2. Определяем реакцию в заделке МêÀ, записав уравнение равновесия стержня (рисунок 1.5, б):

ΣMк = MкА − M l − M − 3M + 2M 2l = 0 .
l	l

Величина реакции МêÀ = Ì.

3.Эпюру крутящего момента получаем методом сечений. Стержень имеет три силовых участка. Необходимо определить крутящий момент в 6 сечениях, расположенных в начале и конце каждого из участков (рисунок 1.5, в).

Схемы равновесия отсеченных частей, уравнения равновесия и полученные значения крутящего момента по сечениям приведены в таблице 1.4.

4.По полученным данным с учетом правила знаков строим эпюру крутящего момента в стержне (рисунок 1.5, г).

Таблица 1.4

Сечение

Схема равновесия отсеченной части, уравнение равновесия и величина крутящего момента

					M	MêI
I
ΣM	к	= M	кI	+ M = 0			MêI = –M
					M/l
					M		MêII
II
ΣM	к	= M	кII		+ M − M l = 0		MêII = 0
					l
					M/l	M
					M		MêIII
III
ΣM	к	= M	кIII		+ M − M l − M = 0		MêIII = M
					l

19

						Окончание таблицы 1.4
Сечение		Схема равновесия отсеченной части, уравнение
		равновесия и величина крутящего момента
					M/l
				M	M			MêIV
IV
ΣM	к	= M	кIV	+ M − M l − M = 0				MêIV = M
					l
				M/l
			M		M	3M		MêV
V
ΣM	к	= M	кV	+ M − M l − M − 3M = 0				MêV = 4M
					l
		M/l		M	3M		2M/l
M								MêVI
VI
ΣM	к	= M	кVI	+ M − M l − M − 3M +			2M	2l = 0 MêVI = 0
					l		l

1.4. Прямой поперечный изгиб балки

Стержень, работающий в условиях изгиба, принято называть балкой. Прямой изгиб — это вид деформации, при котором внешние усилия приложены к балке перпендикулярно ее продольной оси и действуют в плоскости, совпадающей с одной из главных плоскостей инерции поперечного сечения балки. В поперечных сечениях балки возникают изгибающий момент

20

M и поперечная сила Q, действующие в той же плоскости, что и внешние силы. Если в сечениях возникают оба внутренних силовых фактора, то такой изгиб называют прямым попереч- ным. Если же в сечениях возникает только изгибающий момент, то это прямой чистый изгиб.

При прямом изгибе строят эпюры поперечной силы ЭQ и изгибающего момента ЭM. Для построения эпюр используют метод сечений. При действии распределенных нагрузок эпюры строят с помощью уравнений внутренних силовых факторов на грузовых участках — уравнений сил Q(z) и моментов M(z). Ось z является продольной осью балки.

При построении эпюры поперечной силы следует иметь в виду следующие закономерности:

—в сечении, где приложена сосредоточенная внешняя сила, на эпюре поперечной силы происходит скачок на вели- чину внешней силы;

—на участке балки между сосредоточенными внешними силами поперечная сила не изменяется;

—на участке, где действует равномерно распределенная внешняя нагрузка, поперечная сила изменяется по линейному закону;

—действующие внешние моменты не влияют на эпюру поперечной силы.

Основные закономерности при построении эпюры изгибающего момента:

—в сечении, где приложена сосредоточенная внешняя сила, на эпюре изгибающего момента происходит перелом (изменяется угол наклона к продольной оси балки);

—на участке балки между сосредоточенными внешними силами изгибающий момент изменяется по линейному закону;

—на участке, где действует равномерно распределенная внешняя нагрузка, изгибающий момент изменяется по параболическому закону;

—в сечении, где приложен сосредоточенный внешний момент, на эпюре изгибающего момента происходит скачок;

—на участке балки между сосредоточенными внешними моментами эпюра изгибающего момента постоянная.

21

Пример 3

Для балки, показанной на рисунке 1.6, нагруженной сосредоточенными внешними силами и моментами, построить эпюры внутренних силовых факторов (поперечной силы Q в долях ql и изгибающего момента M в долях ql2). Размеры участков балки и величины действующих сил и моментов приведены в таблице 1.5.

M1			M2	M3
l1	P1	l2	P2	l
	Рисунок 1.6

						Таблица 1.5
l1	l2	P1	P2	M1	M2		M3
l	2l	–3ql	–ql	ql2	3ql2		–2ql2

Решение

1.Изображаем реальную схему задачи с учетом длин уча- стков, величин и направлений действующих сил и моментов в соответствии с данными таблицы 1.5 (рисунок 1.7, а).

2.Направляем ось z вдоль продольной оси балки и опреде-

ляем реакции опор RyÀ è RyB, используя уравнения равновесия (рисунок 1.7, б):

ΣPy = RyА + RyB + 3ql − ql = 0,

ΣMA = −ql2 + 3ql l − 3ql2 − ql 3l + 2ql2 + RyB 4l = 0.

Решив систему уравнений, получаем значения реакций:

RyА = 0,5ql, RyВ = −2,5ql .

22

ql2	3ql2	2ql2
3ql		ql
l	2l	l

à

RyA

ql2

3ql2

2ql2

RyB

A

3ql

ql

B

z

á

I

II III

IV

V

VI

0,5ql

ql2

3ql2

2ql2

2,5ql

3ql

ql

â

0,5ql	+
			ÝQ
	0,5ql	–
–
2,5ql
	2,5ql2		2ql2
ql2		+
		0,5ql2	ÝM
	–
1,5ql2
	ã
	Рисунок 1.7

23

3.Эпюры поперечной силы и изгибающего момента строим с использованием метода сечений. Балка имеет три силовых участка. Необходимо определить внутренние силовые факторы

â6 сечениях, расположенных в начале и конце каждого из уча- стков (рисунок 1.7, в).

Схемы равновесия отсеченных частей, уравнения равновесия и полученные значения поперечной силы и изгибающего момента по сечениям приведены в таблице 1.6.

4.По полученным данным с учетом правил знаков для поперечной силы и изгибающего момента строим эпюры поперечной силы и изгибающего момента в балке (рисунок 1.7, г).

Таблица 1.6

Схема равновесия отсеченной части, уравнения Сечение равновесия и величины поперечной силы

и изгибающего момента

ql2

QI

I

2,5ql

MI

ΣPy

= −2,5ql + QI = 0,

QI = 2,5ql,

ΣMA = −ql2 + MI = 0

MI = ql2

ql2

QII

II

2,5ql

MII

ΣPy = −2,5ql + QII = 0,

QII = 2,5ql,

MII = –1,5ql2

ΣMA = −ql2 + QII l + MII

= 0

ql2

QIII

III

2,5ql

3ql

MIII

ΣPy

= −2,5ql + 3ql + QIII = 0,

QIII = –0,5ql,

MIII = –1,5ql

2

ΣMA = −ql2 + 3ql l + QIII l + MIII = 0

24

Окончание таблицы 1.6

Схема равновесия отсеченной части, уравнения Сечение равновесия и величины поперечной силы

и изгибающего момента

ql2

QIV

IV

2,5ql

3ql

MIV

QIV = –0,5ql,

ΣPy

= −2,5ql + 3ql + QIV = 0,

ΣMA = −ql2 + 3ql l + QIV 3l + MIV = 0

MIV = –0,5ql2

ql2

3ql2

QV

V

2,5ql

3ql

ql

MV

QV = 0,5ql,

ΣPy

= −2,5ql + 3ql − ql + QV = 0,

ΣMA = −ql2 + 3ql l − 3ql2 − ql 3l +

MV = 2,5ql2

+ QV 3l + MV = 0

ql2

3ql2

QVI

VI

2,5ql

3ql

ql

MVI

QVI = 0,5ql,

ΣPy

= −2,5ql + 3ql − ql + QVI = 0,

ΣMA = −ql2 + 3ql l − 3ql2 − ql 3l +

MVI = 2ql2

+ QVI 4l + MVI = 0

На каждой схеме равновесия отсеченной части неизвестная поперечная сила в сечении направлена вверх. По правилу знаков она считается отрицательной. Поэтому для всех полу- ченных по сечениям величин поперечной силы следует изменить знак на противоположный.

В каждом сечении неизвестный изгибающий момент направлен против хода часовой стрелки. Он вызывает сжатие верхних волокон сечения и по правилу знаков считается положительным. Поэтому для всех полученных по сечениям вели- чин изгибающего момента знак не изменяется.

25

Пример 4

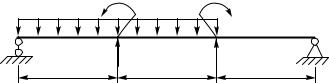
Для балки, показанной на рисунке 1.8, нагруженной сосредоточенными силами и моментами и равномерно распределенной нагрузкой, построить эпюры внутренних силовых факторов (поперечной силы Q и изгибающего момента M). Размеры участков балки, величины действующих сил, моментов и интенсивности распределенной нагрузки приведены в таблице 1.7.

M1	aq	M2
	P1	P2
l1	l2	l
	Рисунок 1.8

Таблица 1.7

l1	l2	P1	P2	M1	M2	a
l	2l	–3ql	–ql	ql2	–3ql2	–2

Решение

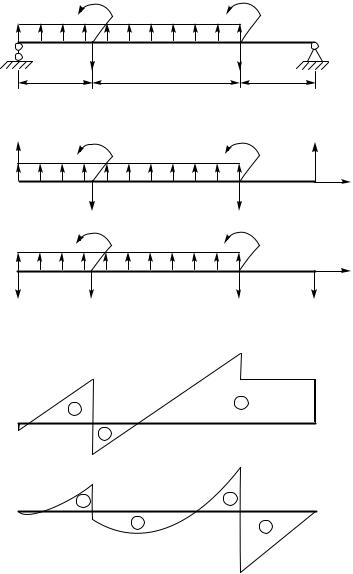
1.Изображаем реальную схему задачи с учетом длин участков, величин и направлений действующих нагрузок в соответствии с данными таблицы 1.7 (рисунок 1.9, а).

2.Направляем ось z вдоль продольной оси балки и опреде-

ляем реакции опор RyÀ è RyB, используя уравнения равновесия (рисунок 1.9, б):

ΣPy = RyА + RyB − 3ql − ql + 2q 3l = 0,

ΣMA = ql2 + 3ql2 + 2q 3l 1,5l − 3ql l − ql 3l + RyB 4l = 0.

Решая систему уравнений, получаем значения реакций:

RyА = −0,25ql, RyВ = −1,75ql .

26

ql2

2q

3ql2

3ql		ql
l	2l	l

à

R A	ql2		2q	3ql2	R	B
y					y
A		3ql		ql		B	z
	ql2		2q	3ql2
0,25ql		3ql		ql	1,75ql		z
				á
					2,75ql
		1,75ql					1,75ql
		+			+
		–					ÝQ
0,25ql	1,25ql
					1,25ql2
		0,75ql2		+
		+
							ÝM
			–
0,016ql	2	0,25ql2			–
		0,64ql2
				1,75ql2

â

Рисунок 1.9

27

3. Балка имеет три силовых участка. Для построения эпюр поперечной силы и изгибающего момента получим уравнения сил и моментов для силовых участков. Для каждого из участков записываем уравнения Q(z) и M(z), описывающие изменение внутренних силовых факторов в зависимости от координаты z.

Начало координат выбираем в точке А. На первом участке балки переменная z (координата сечения) изменяется в пределах 0 ≤ z ≤ l, на втором участке — l ≤ z ≤ 3l, на третьем — 3l ≤ z ≤ 4l. На каждом из участков выбираем сечение на произвольном расстоянии z от начала координат. В этом сечении в соответствии с методом сечений

а) рассекаем балку, б) отбрасываем правую часть,

в) прикладываем неизвестные внутренние силовые факторы Q и M,

г) записываем уравнение равновесия.

Так как сечение расположено на произвольном расстоянии z от начала координат, то в получаемых уравнениях равновесия поперечная сила и изгибающий момент будут представлены в виде функций от переменной z.

Для 1-го силового участка балки уравнения равновесия отсеченной части:

ΣPy = −0, 25ql + 2q z + QI (z) = 0,

ΣMA = 0, 25ql z − 2q z z + MI (z) = 0. 2

Получаем уравнения сил и моментов для этого участка:

QI (z) = 0, 25ql − 2qz,

MI (z) = −0, 25qlz + 2q z2 . 2

Аналогичным образом получаем уравнения сил и моментов для 2-го и 3-го силовых участков балки.

Схемы равновесия отсеченных частей, уравнения сил и моментов и полученные значения поперечной силы и изгибающего момента в начале и конце каждого из силовых участков балки приведены в таблице 1.8.

28

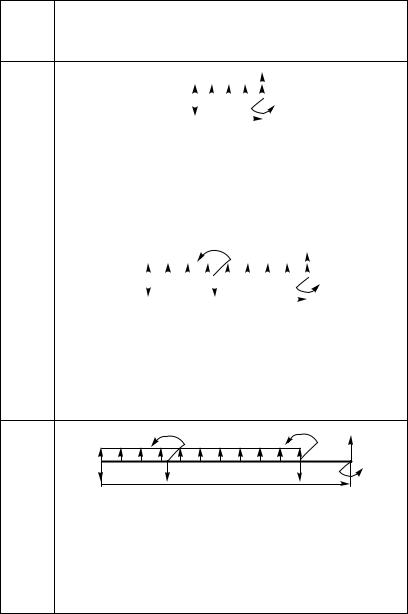
Таблица 1.8

Схема равновесия отсеченной части, уравнения сил Участок и моментов и величины поперечной силы

и изгибающего момента

2q

QI(z)

A

MI(z)

0,25ql

z

I

Q(z) = 0, 25ql − 2qz,

z2

M (z) = −0, 25qlz + 2q

,

2

z = 0: QI(0) = 0,25ql,

MI(0) = 0

z = l: QI(l) = –1,75ql, MI(l) = 0,75ql2

A

ql2

2q

QII(z)

0,25ql

3ql

z

MII(z)

II

Q(z) = 0, 25ql + 3ql − 2qz,

z2

M (z) = −0, 25qlz − ql2

− 3ql(z − l) + 2q

2

z = l:

QII(l) = 1,25ql, MII(l) = –0,25ql2,

z = 3l: QII(3l) = –2,75ql, MII(3l) = 1,25ql2

	ql2	2q	3ql2	QIII(z)
A
0,25ql	3ql	z	ql	MIII(z)

	III	Q(z) = 0, 25ql + 3ql + ql − 2q 3l,
		M (z) = −0, 25ql z − ql2 − 3ql (z − l) − 3ql2 −
		− ql (z − 3l) + 2q 3l (z −1,5l)

z= 3l: QIII(3l) = –1,75ql, MIII(3l) = –1,75ql2,

z= 4l: QIII(4l) = –1,75ql, MIII(4l) = 0

29

4.По полученным данным строим эпюру поперечной силы

âбалке (рисунок 1.9, в). При этом, как и в предыдущем примере, учитываем правило знаков: для всех полученных по уча- сткам величин поперечной силы меняем знак на противоположный.

5.В соответствии с дифференциальной зависимостью Д. И. Журавского

dM (z) = Q(z) , dz

в сечениях балки, где поперечная сила Q равна нулю, на эпюре изгибающего момента будет локальный экстремум — на 1-м и 2-м участках. Определим координаты сечений и значения изгибающего момента М в этих сечениях. По уравнению сил для каждого из участков определим соответствующую координату точки, в которой поперечная сила Q равна нулю. Затем подставим полученное значение координаты z в уравнение моментов для этого участка и найдем искомую величину изгибающего момента в точке экстремума.

Первый участок:

QI (z) = 0, 25ql − 2q z = 0,

z = 0,125l,

MI (0,125l) = −0, 25ql 0,125l + 2q (0,125l)2 ≈ −0,016ql2. 2

Второй участок:

QII (z) = 0, 25ql + 3ql − 2q z = 0,

z = 1,625l,

MII (1,625l) = −0, 25ql 1,625l − ql2 − 3ql (1,625l − l) +

+ 2q (1,625l)2 ≈ −0,64ql2. 2

По полученным данным с учетом правила знаков строим эпюру изгибающего момента в балке (рисунок 1.9, в).

30