Список индивидуальных данных

Таблица 1.1

Вариант	1	2	3	4	5	6	7	8	9	10
f1, кГц	2	10	14	20	24	30	36	40	44	50
Xm1	0,2	2,5	0,8	1,6	1,8	2,6	3,8	0,6	2,4	3,6
Fд	12 f1	12 f1	12 f1	12 f1	12 f1	12 f1	12 f1	12 f1	12 f1	12 f1
Вариант	11	12	13	14	15	16	17	18	19	20
f1, кГц	4	8	10	2	12	14	32	36	40	42
Xm1	0,5	2,6	3,2	0,9	1,6	3,4	3,2	2,6	2,4	0,9
Fд	12 f1	12 f1	12 f1	12 f1	12 f1	12 f1	12 f1	12 f1	12 f1	12 f1
Вариант	21	22	23	24	25	26	27	28	29	30
f1, кГц	50	46	48	34	32	30	24	26	28	12
Xm1	1,8	2,7	3,6	1,4	0,7	0,8	1,6	3,2	3,1	2,3
Fд	12 f1	12 f1	12 f1	12 f1	12 f1	12 f1	12 f1	12 f1	12 f1	12 f1

Пример выполнения работы

1. Моделирование сигнала

Для выполнения заданий №1-5 необходимо смоделировать гармонические сигналы с различными параметрами. В данном УМК все приведенные в курсе лабораторных работ листинги программ выполнены в программной среде MATLAB.

При моделировании сигнала в системе MatLabследует сначала задать параметры сигнала, затем вычислить вектор значений моментов времени, для которых будут определяться значения сигнала.

Пример:

2. Для расчета математического ожидания и дисперсии сигналов (задание №6) необходимо воспользоваться формулами (1.1) и (1.2).

3. Для выполнения задания №7 необходимо выполнить рассчет частотных характеристик сигналов. Расчет выполняется в базисе Фурье. Ниже приведен листинг программы, реализующей алгоритм расчета трансформант Фурье (1.4) и вычисление значений энергии сигнала (1.8). Для расчета амплитудной и фазовой характеристик необходимо воспользоваться формулами (1.6) и (1.7) соответственно.

4. Для выполнения задания №4 необходимо изменяя параметры nиNрассчитать энергетические спектры сигналов по формуле (1.8) и произвести сопоставитьельный анализ полученных результатов.

Контрольные вопросы к защите

1. Понятие дискретного сигнала.

Дискретный сигнал - информационный сигнал. Сигнал называется дискретным, если он может принимать лишь конечное число значений.

2. Теорема Котельникова.

3. Статистические параметры сигналов (математическое ожидание, дисперсия).

4. Частотный анализ сигналов.

5. Понятие нормированной частоты.

6. Дискретное преобразование Фурье (прямое и обратное).

Прямое преобразование:

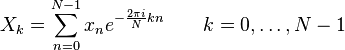
Обратное преобразование:

7. Представление чисел в комплексной форме.

Способ оценки результатов

Оценка производится по зачетной системе.

Зачет за выполнение лабораторной работы ставится за правильно выполненную работу и правильные ответы на контрольные вопросы. Не зачитывается работа в том случае, если не выполнено хотя бы одно из заданий работы, или при выполнении допущены грубые ошибки.

Лабораторная работа №2. Вариационный метод частотного анализа

Требования к содержанию, оформлению и порядку выполнения

Отчет о выполнении лабораторной работы должен содержать все выполненные задачи и ответы на контрольные вопросы.

Теоретическая часть

В данной работе рассматривается вариационный метод частотного анализа.

В настоящее время в большинстве алгоритмов процедура анализа частотных характеристик реализуется на основе алгоритма быстрого преобразования Фурье (БПФ) с равноразнесенными частотами анализа.

Рассмотрим новый метод вычислений долей энергии отрезков сигналов, соответствующим заданным частотным диапазонам. Основная суть метода заключается в следующем.

Пусть компоненты вектора представляют собой значения некоторого сигнала (функции времени)

. (2.1)

Трансформанта Фурье отрезка отсчетов сигнала (вектора), в качестве области определения которой естественно рассматривать (нормированная частота)

, (2.2)

Из равенства Парсеваля нетрудно получить долю энергии отрезка сигнала, соответствующую частотному интервалу

(2.3)

Если в правую часть соотношения (2.3) подставить определение (2.2), то в результате преобразований получим

, (2.4)

где – симметричная матрица, элементы которой определяются

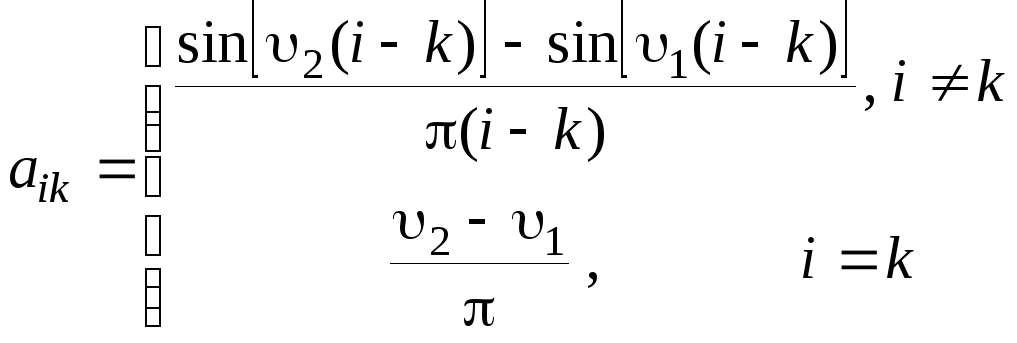(2.5)

Таким образом, долю энергий отрезка сигнала в любом частотном интервале можно вычислить на основе представления (2.4), не вычисляя при этом соответствующую трансформанту Фурье. Матрицу вида естественно называть субполосной матрицей.

Вычисления для полного набора частотных интервалов

Полным набором называется совокупность частотных интервалов

(2.6)

которые полностью покрывают всю частотную ось.

Если при вычислениях долей энергии отрезка сигнала вида (2.1) во всех частотных интервалах, например в случае вычислений спектрограмм, основываться непосредственно на квадратичных формах вида (2.4), то объем реализуемых вычислений будет пропорционален величине , то есть слишком большим.

При многократной реализации вычислений с одним и тем же набором частотных интервалов и длительностей обрабатываемых отрезком данных целесообразно использовать следующий подход.

Для всех введём обозначения

,

причём справедливы аналоги представления (2.4)

, (2.7)

где ;

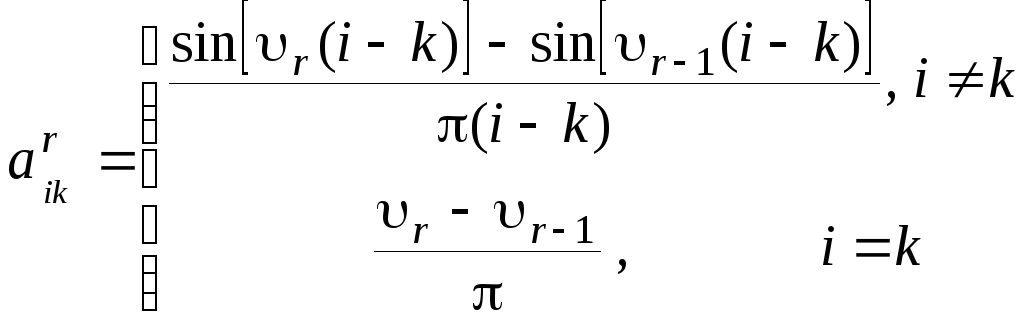, (2.8)

где

Пусть далее – матрица собственных векторов матрицы

, (2.9)

такая , что выполнятся соотношение

где

,

причём предполагается упорядочение собственных чисел по убыванию

.

Положим

.

Тогда представление (2.7) нетрудно преобразовать к виду

. (2.10)

Вычисления показывают, что выбор количества слагаемых в (2.10) на основе соотношения

, (2.11)

при выполнении условия

позволяет на основе соотношения (2.10) оценивать доли энергии отрезков сигналов с погрешностями, не превышающими нескольких сотых долей процента.

При равноразнесенных интервалах анализа выражение (2.11) имеет вид

Тогда вычисление всей совокупности долей энергии отрезка сигнала потребует порядка вычислительных операций типа «умножение», что может быть существенно меньше чем правая часть (2.4).

Для вычислений можно составить блочную матрицу вида

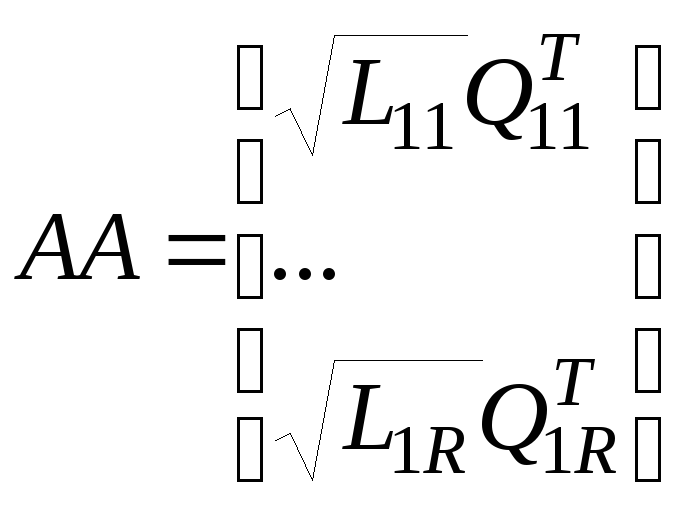, (2.12)

где ,.

Далее следует вычислить вектор

. (2.13)

Тогда с заданной точностью выполняется равенство

. (2.14)

Таким образом, основой вычислений полного набора долей энергии отрезка сигнала могут служить соотношения (2.13) и (2.14).