матан 3 курс 2013 / лекции / Невизначений інтеграл / лекция № 4

МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

ГОРЛІВСЬКИЙ ТЕХНІКУМ ДОНЕЦЬКОГО НАЦІОНАЛЬНОГО УНІВЕРСИТЕТУ

ЛЕКЦІЯ № 4

з теми: «Інтегрування деяких ірраціональностей.»

Модуль КЗН-02. ПР.О.03.07 Невизначений інтеграл.

Дисципліна: «Математичний аналіз»

Розглянуто та схвалено на засіданні циклової комісії інформаційних технологій та прикладної математики. Протокол № ____ від _______20__ р. Голова циклової комісії ПМ Велікодна О. В.

Розробив викладач Велікодна О. В.

ПЛАН ЗАНЯТТЯ

Дата: курс: ІІI

Викладач: Велікодна Ольга Володимирівна.

Тема: Інтегрування деяких ірраціональностей.

Мета:

• Дидактична: навчитися обчислювати первісну, володіти методами інтегрування, знаходити первісну раціональних функцій, трансцендентних та ірраціональних функцій.

• Виховна: виховувати професійно спрямовану особистість, здатну чітко та логічно висловлювати та доводити свої думки.

• Методична: вдосконалювати методику проведення лекції з використанням методики пошукової технології.

Тип: лекція

Вид: лекція – дослідження.

Методи та форми проведення заняття: словесні, наглядні, проблемно – пошукові.

Науково-методичне забезпечення:

1. Кудрявцев Л.Д. Курс математического анализа: Учебник. Для студентов университетов и вузов. В 3 т. - М.: Высшая школа,1998.

2. Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989.

3. Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для вузов. - М.: Наука. Гл. ред. физ. - мат. лит.,1975.

4. Марон А. И. Дифференциальное и интегральное исчисление функции одной переменной в примерах и задачах. – М.: Наука, 1973.

Між предметні зв’язки:

• Дисципліни, що забезпечують: елементарна математика

• Дисципліни, що забезпечуються: дискретна математика, диференціальні рівняння, рівняння математичної фізики, чисельні методи, методи оптимізації, теорія функцій комплексної змінної.

Обладнання: зошити, ручки, крейда, дошка.

ХІД ЗАНЯТТЯ

1. Організаційна частина:

1. відсутні;

2. підготовка до заняття;

3. перевірка д/з.

2. Актуалізація опорних знань: поняття ірраціональної функції, таблиця інтегралів, основні методи інтегрування.

3. Вивчення нового матеріалу:

• Тема лекції: Інтегрування деяких ірраціональностей.

• Мотивація вивчення матеріалу: вивчити основний математичний апарат – невизначений інтеграл, що дає змогу розв’язувати прикладні задачі в різних галузях науки та техніки.

• План вивчення нового матеріалу: надається в конспекті лекції.

4. Виклад нового матеріалу. Конспект лекції надається.

5. Закріплення нового матеріалу.

6. Підсумки заняття.

7. Домашнє завдання:

Конспект лекції № 4.

Тема: Інтегрування деяких ірраціональностей.

План лекції № 4.

1. Інтеграли виду .

2. Інтегрування диференційного біному.

1. Розглянемо інтеграл . Будемо вважати, що числа r, …, rраціональні та записані з однаковим знаменником: , m – натуральне число, pі – цілі числа, визначник (якщо визначник дорівнює 0, то функція приводиться до раціональної). Зробимо в інтегралі заміну змінної , звідки отримаємо . Функція ρ(t) – раціональна функція, ρ′(t) – також раціональна функція. . = , де R٭(t) – раціональна функція. Таким чином, заміна змінного зводить інтеграл до інтегралу від раціональної функції. До розглянутого типу інтегралів відносять також інтеграли виду , зокрема інтеграли .

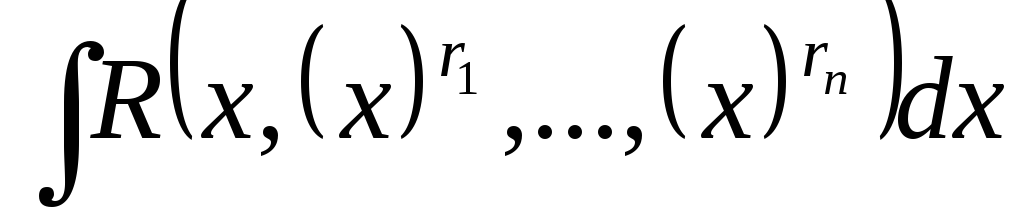Приклад.

Обчислити інтеграл .

В інтегралі робимо заміну змінної t² = х, t > 0, тому dх = 2tdt. Далі маємо:

2. Розглянемо інтеграл виду ; його підінтегральний вираз називається диференційним біномом. Будемо вважати, що α, β, γ – раціональні числа, a, b – вільні дійсні числа.

Зробимо в інтегралі заміну змінного x = t, тоді , та відповідно = . Таким чином, інтеграл за допомогою заміни зводиться до інтегралу виду , де a та λ – раціональні числа, .

Розглянемо три випадки.

1. α – ціле число. λ = m/n, m та n > 0 – цілі числа. Тоді робимо заміну u = t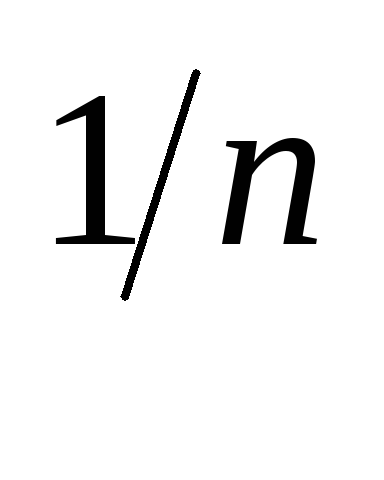, яка зведе інтеграл до інтегралу від раціональної функції.

2. λ – ціле число. α = m/n, m та n > 0 – цілі числа. Тоді робимо заміну u = (a + bt)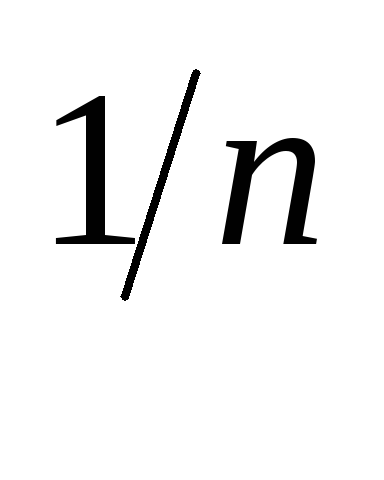, яка зведе інтеграл до інтегралу від раціональної функції.

3. α + λ – ціле число. α = m/n, m та n > 0 – цілі числа. Тоді маємо: , далі інтеграл заміною зводиться до інтегралу від раціональної функції.

Маємо, що в трьох розглянутих випадках інтеграл від диференційного біному зводиться до інтегралу від раціональної функції. Тому, якщо хоча б одно з чисел α, , в начальному інтегралі є цілим числом, то цей інтеграл зводиться до інтегралу від раціональної функції, тобто виражається через елементарні функції. Ні в яких інших випадках інтеграл не виражається через елементарні функції.

Квадратичні ірраціональності

Розглянемо деякі типи інтегралів, що містять ірраціональні функції.

Інтеграли типу, називають невизначеними інтегралами від квадратичних ірраціональностей. Їх можна знайти таким чином: під радикалом виділити повний квадрат

і зробити підстановку . При цьому перші два інтеграли приводяться до табличних, а третій – до суми двох табличних інтегралів.

Приклад 1. Знайти інтеграли .

 Оскільки , то .

Зробимо підстановку, , . Тоді

. 

Приклад 2. Знайти інтеграл .

 Оскільки , то підстановка має вигляд , ,. Тоді

. 

Інтеграли типу, де - многочлен степеня можна обчислювати, користуючись формулою

(5.1)

де - многочлен степеня з невизначеними коефіцієнтами, – також невизначений коефіцієнт.

Всі невизначені коефіцієнти знаходяться з тотожності, отриманої диференціюванням обох частин рівності (5.1):

, після чого необхідно прирівняти коефіцієнти при однакових степенях невідомої .

Приклад 3. Знайти інтеграл

 По формулі (5.1) маємо:

.

Диференціюючи цю рівність, отримаємо:

, тобто

,

. Порівнюємо коефіцієнти при однакових степенях :

, при

при

при

Звідси . Отже

. 

Дробово-лінійна підстановка

Інтеграли виду , де - дійсні числа, – натуральні числа, зводяться до інтегралів від раціональної функції шляхом підстановки , де – найменше спільне кратне знаменників дробів .

Дійсно, з підстановки виходить, що і , тобто і виражаються через раціональні функції від . При цьому і кожний степінь дробу виражається через раціональну функцію від .

Приклад 4. Знайти інтеграл .

 Найменше спільне кратне знаменників дробів і є 6. Тому вважаємо , , , . Отже

. 

Приклад 5.Вказати підстановку для знаходження інтегралів:

 Для підстановка , для підстановка . 

Тригонометрична підстановка

Інтеграли типу зводяться до інтегралів від функцій, раціонально залежних від тригонометричних функцій, за допомогою наступних тригонометричних підстановок: для першого інтеграла; для другого інтеграла; для третього інтеграла.

Приклад 6. Знайти інтеграл .

 Покладемо , , . Тоді

. 

Інтеграли виду

Тут підінтегральна функція є раціональною функцією відносно і . Виділивши під радикалом повний квадрат і зробивши підстановку , інтеграли вказаного типу приводяться до інтегралів вже розглянутого типу, тобто до інтегралів типу, . Ці інтеграли можна обчислити за допомогою відповідних тригонометричних підстановок.

Приклад 7. Знайти інтеграл .

 Оскільки , то , , . Тому . Покладемо , . Тоді

.

Зауваження: Інтеграл типу доцільно знаходити за допомогою підстановки .

Інтегрування диференціального бінома

Інтеграли типу (названі інтегралами від диференціального бінома), де – дійсні числа; – раціональні числа, беруться, як показав Чєбишев П.А., лише у разі, коли хоча б одне з чисел , або є цілим.

Раціоналізація інтеграла в цих випадках здійснюється наступними підстановками:

1) якщо - ціле число, то підстановка , де – найменше спільне кратне знаменників дробів і ;

2) якщо - ціле число, то підстановка , де - знаменник дробу .

3) якщо - ціле число, то підстановка , де - знаменник дробу .

У всій решті випадків інтеграли типу не виражаються через відомі елементарні функції, тобто не «беруться».

Приклад 8. Знайти інтеграл . Оскільки то, , . Тому робимо підстановку . Таким чином,

. 