7.3 Обратное дискретное преобразование Фурье

Перейдем к получению обратного дискретного преобразования Фурье (ОДПФ) .

Умножим обе части выражения ДПФ (3) на и просуммируем по k от 0 до N-1.

(6).

При этом мы учли, что поскольку суммирование по k ведется в пределах от 0 до N-1, то, согласно (5) сумма будет отлична от нуля только при n-n’=0 т.е. при n=n’. Переобозначив n’ на n и выразив из (6) x(n) , получим выражение для ОДПФ, которое совместно с выражением (3) для ДПФ дает дискретную форму преобразования Фурье:

(7a)

(7b)

Т.к. при выборе постоянных множителей у прямого и обратного преобразований Фурье должно соблюдаться условие постоянства их произведения, то для упрощения записи отбросим множитель T у прямого и 1/T у обратного преобразования, что приведет к следующей форме ДПФ:

(8а)

(8б)

Введя для комплексной экспоненты обозначение , дискретное преобразование Фурье представим в виде:

(9а)

(9б)

Последняя форма будет выглядеть еще проще в матричном представлении:

Х=Тх (10а)

x=Т’X (10б)

где элементами матрицы T являются комплексные экспоненты , а матрицы Т’ .

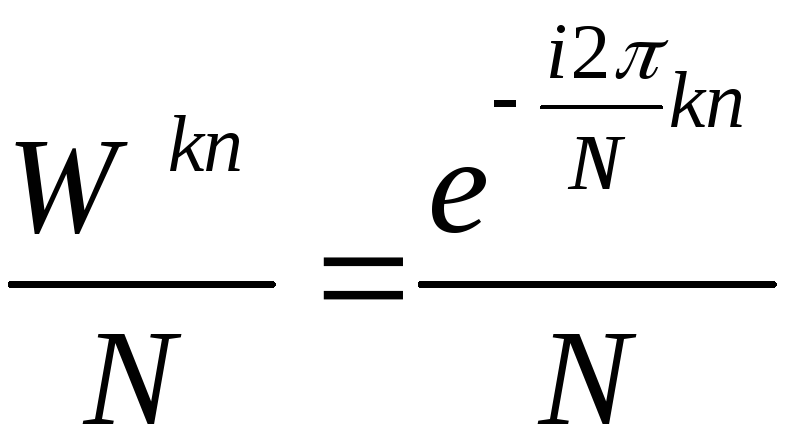Очевидна связь между матрицами T и Т’:

Выпишем для примера матрицы прямого и обратного преобразования Фурье для одно, двух, трех, четырехточечных последовательностей.

1) N=1.

2)N=2.

3)N=3.

4)N=4.

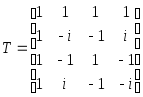
Сделаем несколько важных замечаний относительно дискретного преобразования Фурье.

1. Поскольку система экспонент ортогональна на дискретном множестве N точек, независимо от выбора начальной точки этого множества, то начальное значение индексов суммирования в (7) и (9) могут быть любыми, лишь бы разность между начальными и конечными значениями была равна N.

2. Последовательности x(n) и X(k), определяемые формулами 7 или 9, вне множества 0....N-1 являются N-периодическими, т.е.

x(rN+n)=x(n)

X(rN+k)=X(k)

где р-любое число, n и k -целое в промежутке от 0 до N-1. Это свойство является следствием N-периодичности экспонент (8): Так, например, для ОДПФ получим

3. Согласно предыдущему замечанию, X(-k)=X(n-k).

Действительно,

Т.е. X(-1)=X(N-1);X(-2)=X(N-2) и т.д.

Таким образом, второй половине преобразования Фурье, т.е. значениям X(k) при k>N/2 соответствуют отрицательные частоты.

Чтобы увидеть непрерывный аналог преобразования Фурье, рассчитанного дискретным способом, когда n и k изменяются от 0 до N-1, нужно “ разрезать” дискретный образ Фурье в точке N/2 и часть X(k), соответствующую k>N/2 поставить перед первой половиной. При этом чтобы перейти к реальным значениям частот при формировании оси частот нужно умножать частотный отсчет k на величину частотного интервала в герцах. Таким образом, значение частоты на k-ом отсчете равно .

то x₃(n)~X ₃(k), где X ₃(k)=X ₁(k)+X ₂(k).

Если последовательности x₁(n) и x₂ (n) имеют разную длину, соответственно N₁ и N₂, то длина N₃=max(N₁,N₂).

Последовательность меньшей длительности следует дополнить нулями.

2.Свойство сдвига.

2.1Сдвиг во временной области.

Если x(n)~X(k) , то x(n-h)~W ^-kh X(k)

Доказательство:

Используя определение прямого ДПФ в виде (9б) и делая замену пере-

менной суммирования n-h =r или n=r+h, получим:

2.2 Сдвиг в частотной области.

Если x(n)~X(k) , то x(n)W^nf ~ X(k-f)

Доказательство этого свойства, аналогичное предыдущему, основано на

определении ОДПФ (7б) или (9б).

3.Свойство комплексной сопряженности

Если x(n), где n=0,1,2,..N-1- п

оследовательность действитель- *

ных чисел ,а N-четное,и x(n)~X(k) ,то X(N/2+r)=X (N/2-r), где

r=0,1,..N/2.

Доказательство:

Примеры:

1) Коэффициенты ДПФ последовательности 8-ми действительных чисел соответственно равны X(0)=5, X(1)=i, X(2)=1+i,X(3)=2+3i,X(4)=2.

Найти значения коэффициентов X(k), k=5,6,7.

Ответ: Согласно свойству (3) X(5)=2+3i,X(6)=1+i,X(7)=i.

2) Показать, что ДПФ N-точечной последовательности

{x(n)}={А,А,...А} есть последовательность N-точечная

последовательность {X(k)}={NА,0,0...)}.

Решение:

Согласно определению прямого ДПФ (7а) и свойству ортогональности

экспонент (4)

7.5Теорема Парсеваля. Спектр мощности

Теорема Парсеваля для конечной временной последовательности имеет

вид:

(11)

Величину

(12)

мы назвали спектром мощности.

В силу свойства 3 комплексной сопряженности, спектр мощности будет симметричным относительно k=N/2. Т.к. значения N/2<k<N

соответствуют отрицательным частотам,не имеющим физического

смысла, то весь смысл спектра мощности как вклада в общую мощность

конкретных частот, содержится в первой половине спектра,

соответствующего положительным частотам, т.е. значениям 0<k<N/2.

Важной особенностью спектра мощности является ее инвариантно-

сть к сдвигам N-периодической временной последовательности x(n).

Действительно, т.к. согласно свойству сдвига 2.1 x(n-h)_~W^-khX(k),то

C помощью спектра мощности определяется амплитудный спектр:

(13).

Амплитудный спектр также инвариантен к сдвигам временной последовательности x(n) т.к.

p(k) как и Р(k) симметрична относительно k=N/2.

Т.к. образ Фурье X(k) даже для действительной последовательности есть комплексная величина, то чтобы сохранить всю информацию об исходной временной последовательности, наряду с амплитудным спектром нужно вычислить фазовый спектр ,который определяется следующим образом:

(14),

где I(k) и R(k) - действительная и мнимая части X(k).

Согласно свойству 3 комплексной сопряженности R(N/2+r)=R(N/2-r), a I(N/2+r)=-I(N/2-r). Поэтому фазовый спектр оказывается нечетной Функцией относительно k=N/2 т.е. Ф(N/2+r)=-Ф(N/2-r).

Из (14), а также из выражения для ДПФ (7а-9а) следует фундаментальное свойство фазового спектра, заключающееся в инвариантности его относительно умножения на константу.

Если известны амплитудный (13) и фазовый (14) спектры сигнала, позволяющие совместно рассчитать образ Фурье

(15),

то с помощью ОДПФ (7б-9б) можно восстановить исходный сигнал.

7.6 Дискретная свертка.

Определим свертку двух дискретных последовательностей

x(n) и y(n), каждая длины N ка

к следующую сумму

(12)

При этом может оказаться, что аргумент n-r будет

вне пределов [0,N-1]. В зависимости от того,как определим в этом случае значение x(n-r) или y(n-r) получим разные типы сверток: циклическую и линейную.

Если такие значения находятся из свойства N-периодичности (цикличности) последовательностей x(n) и y(n), то полученная свертка называется циклической.

При этом говорят ,что индекс n-i понимается по модулю N, что как раз и означает, если i-n=k+pN, то x(i-n)=x(k),y(i-n)=y(k). Чтобы отметить этот факт, аргумент n-i заключают в двойные скобки, помечая их одновременно нижним индексом N:

(13)

n=0,.....N-1.

Следующий рисунок иллюстрирует сущность циклической свертки,

Рис.1 Циклическая свертка. Члены последовательности y(i) располагаются в обратном порядке по отношению к x(i) порядке, причем напротив y(i) располагается x(0).Одно значение h(i) получается суммированием всех попарных произведений противостоящих значений.

Отметим еще один важный факт, касающийся дискретной

циклической свертки.

В силу N-периодичности последовательностей x(n) и y(n) и свертка

их будет также периодична с периодом N. Действительно

(14)

Отметим, что если свертываемые последовательности имеют разную длину, то более короткую следует дополнить нулями до длины более длинной, и результирующая свертка будет иметь ту же длину.

Если положить, что вне пределов 0....N-1 последовательности x(n) и y(n) равны нулю, и ,следовательно x(i-n) и y(i-n) равны нулю при отрицательных значениях

, то полученная форма свертки называется линейной.

На рис.2 иллюстрируется ,как вычисляется линейная свертка.

Рис.2 Линейная свертка. Индексы последовательности y(i) возрастают в направлении убывания индексов последовательности x(i). Одно значение h(i) получается суммированием всех попарных произведений пересекающихся противостоящих значений.

При этом , в отличие от циклической, можно производить свертку последовательностей различной длины. Длина линейной свертки будет равна N₁+N₂-1.

Действительно, для вычисления n-го элемента линейной свертки находятся произведения элементов сворачиваемых последовательностей , сумма индексов которых равна n. Поэтому минимальный индекс линейной свертки равен 0, а максимальный - N₁-1+N₂-1=N₁+N₂-2 и количество элементов N₁+N₂+1.

Вычисление линейной свертки последовательностей длины N₁ и N₂ можно

свести к вычислению циклической свертки, если дополнить обе последовательности до длины N₁ +N₂-1 добавлением нулей.

Пример 1: Вычислить линейную свертку последовательностей

{x(n)}={1 2 3 4} и {y(n)}={5 4 3 2 1 }. Ответ:

Пример 2: Вычислить циклическую свертку последовательностей:

{x(n)}={1,2,-1,3} и {y(n)}={-1,1,4,1}.

h(0)=x(i)y(-i)=x(0)y(0)+x(1)y(-1)+x(2)y(-2)+x(3)y(-3)= x(0)y(0)+x(1)y(3)+x(2)y(2)+

x(3)y(1)=

h(1)=x(i)y(1-i)=x(0)y(1)+x(1)y(0)+x(2)y(-1)+x(3)y(-2)= x(0)y(1)+x(1)y(0)+x(2)y(3)

+x(3)y(2)= 5

h(2)= x(r)y(2-r) = x(0)y(2)+x(1)y(1)+x(2)y(0)+ x(3)y(-1) = x(0)y(2)+x(1)y(1)+x(2)y(0)+ x(3)y(3) = 10

h(3)= x(r)y(3-r) = x(0)y(3)+x(1)y(2)+x(2)y(1)+ x(3)y(0) =

При этом учтено, что согласно свойству периодичности

4-х точечной последовательности y(n) с периодом N=4, y(-l)=y(4-l).

Пример 3: Вычислить циклическую и линейную свертки последовательностей:

{x(n)}={1,1,1,1} и {y(n)}={1,1,1,1}.

7.7 Теоремы о свертке.

Далее вместо термина циклическая свертка будем

употреблять термин свертка.

Теорема 1.

Пусть

x(n)~X(k) , y(n)~Y(k),где n,k=0,1,.....N-1.

Тогда

x(n)*y(n)~X(k)Y(k). (14)

Другими словами, свертка временных последовательностей x(n) и

y(n) длины N эквивалентна умножению их образов ДПФ.

Доказательство:

Используя определение прямого ДПФ (9a), дискретной свертки (12) и

свойства сдвига ДПФ 2.1, получим: