Классическая статистика ч2 - Сотский А.Б

	¶P		¶P
DP =		DS +				DV ,	(39.26)
	¶S V		¶V S
	¶T		¶T
DT =		DS +				DV ,	(39.27)
	¶S V		¶V S

где в соответствии с теоремой умножения якобианов и правилом калибровки температурной и энтропийной шкал (см. § 5)

¶P

¶(P,V )

¶(P,V ) ¶(T , S )

¶T

=

=

= -

.

(39.28)

¶(S,V )

¶(T , S ) ¶(S,V )

¶S V

¶V S

Подставляя (39.26) – (39.28)

в (39.25), приходим к выражению

¶T

D S 2

¶T

D S

¶P

+ 2

DV

-

³ 0 .

(39.29)

¶S

V

DV

¶V

S

¶V S

Входящие сюда приращения

S и

V ,

будучи вызванными случайными

воздействиями на малую подсистему со стороны термостата, могут принимать произвольные значения. Из алгебры известно, что необходимым и достаточным условиями выполнения (39.29) при любых

S и V являются неравенства

¶Т

T

¶S V

=

³ 0 ,

(39.30)

CV

¶Т 2

¶T

¶P

¶T

¶P

¶T

¶P

+

=

-

£ 0 ,

(39.31)

¶V S

¶S V

¶V S

¶S

V

¶V S

¶V S

¶S V

где слева в (39.31) стоит дискриминант квадратного уравнения, получаемого приравниванием к нулю левой части (39.29). При записи

(39.31) учтено выражение (39.28).

Условие (39.31) представляет собой неравенство для якобиана

∂(Т, Р)	=	∂(Т, Р)∂(Т,V)	=	T		∂P		£ 0 .
¶(S,V)		¶(T ,V)¶(S,V)
				CV		¶V T

Отсюда, в силу (39.30),

	∂P		£ 0 ,
				(39.32)
	¶V T

то есть, давление при увеличении объема равновесных систем при фиксированной температуре может только убывать.

Неравенство (39.32) и вытекающее из (39.30) CV ³ 0 называются

условиями устойчивости моновариантной термодинамической системы. Систем, не удовлетворяющим этим условиям, не существует.

§ 40 Рассеяние света на флуктуациях плотности

61

Применим теорию флуктуаций к объяснению явления рассеяния света в атмосфере.

Пусть параллельный пучок света падает на некоторый объем газа. Если бы газ был однородным (т. е. имел бы во всех точках одинаковую плотность), то диэлектрическая проницаемость среды не зависела бы от координат. В этом случае рассеяние отсутствовало бы, и среда, через которую проходит излучение, была бы невидимой. Однако благодаря хаотическому движению молекул, в отдельных малых объемах возникают области с пониженной, либо повышенной плотностью вещества. Это вызывает случайную неоднородность пространственного распределения диэлектрической проницаемости. На этих неоднородностях световой пучок рассеивается по всем направлениям, и среда становится видимой сбоку. При этом цвет среды будет определяться длиной волны рассеянного излучения.

Для количественного описания данного явления предположим, что в некотором объеме v диэлектрическая проницаемость среды получила приращение δε . Если на данный объем падает линейно поляризованный свет частоты ω , то при условиях

	δε	<< 1,	v <<	λ3	,
	ε			(2π )3

где λ − длина волны света в среде, для интенсивности рассеянного света может быть записано выражение

	ω 4	cE02 (δε )2 v2 sin2 β
I =				.	(40.1)
		2	2
	c	32π ε r

Здесь c − скорость света			в среде, r	>> λ − расстояние от рассеивающего
объема до	точки	наблюдения,		ε − абсолютная		диэлектрическая
проницаемость	среды,		E0 − амплитудный		вектор	напряженности
электрического поля в падающей волне, β − угол между вектором E0 и
радиусом-вектором r		точки наблюдения (рис.			40.1). Выражение (40.1)

получается в результате приближенного решения интегрального уравнения для вектора Герца, которое можно найти в учебниках по электродинамике.

Будем	считать,	что	причиной	флуктуации ε является		изменение
отношения	N v , за	счет	изменения объема v , который занимают N
молекул. В оптике сплошных сред имеет место соотношение
				N
		ε	= ε0 1 + α		,	(40.2)
где ε0 − диэлектрическая				v
			проницаемость вакуума, α − коэффициент
поляризуемости молекулы.			Поэтому при малой флуктуации объема v из
(40.2) найдем

62

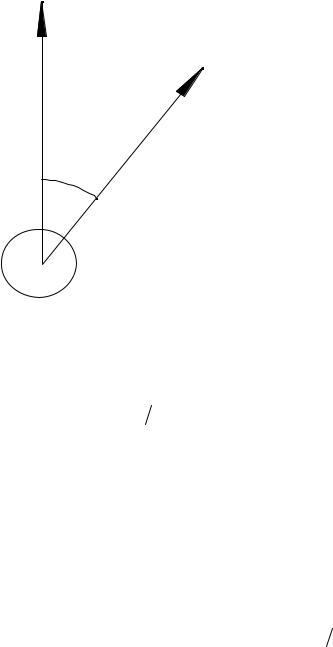
E0

r

β

υ

	Рис. 40.1
	δε (t) = −ε α	N	δ v(t τ	) ,	(40.3)
		v2
	0		1

где t − время, δ v(tτ1 ) − флуктуация объема, τ1 − характерный временной масштаб данной флуктуации. Заметим, что согласно (40.2)

ε α	N	= ε − ε		.	(40.4)
			0
0	v

Предположим, что падающий на рассеивающий объем свет является естественным и создается удаленным источником. Тогда он с высокой точностью может быть описан плоской волной интенсивности

		I	0	= 0.5ε cE2 .		(40.5)
					0
Подставив выражения (40.3)				– (40.5) в (40.1) и заметив, что ω c = 2π / λ ,
найдем
	π 2
I = I0		[δ v(t /τ1 )]2 (1 − ε0 / ε )2 sin2 β .				(40.6)
	λ 4r2
Заметим, что для естественного света направление вектора E0
является случайной функцией					времени. В результате	β = β (t /τ 2 ) , где

τ 2 − характерный временной масштаб изменения данной функции. Таким

образом, интенсивность I вида (40.6) является случайной функцией времени, представленной произведением двух случайных функций. Характерные времена изменения данных функций τ1 и τ 2 гораздо меньше

времени срабатывания большинства детекторов света, в том числе и

63

человеческого глаза. Поэтому в экспериментах обычно наблюдается средняя по времени интенсивность рассеянного света

		~		1		t		[δ v(t /τ1 )]2 sin2[β (t /τ 2 )]dt ,	(40.7)
	I					∫
			τ
где τ >> τ1 , τ >> τ 2 .					t −τ
									δ v(t /τ1 ) и
Чтобы оценить								будем считать случайные функции
						I

β (t /τ 2 ) стационарными (с неизменной во времени статистикой). Тогда для

вычисления I можно воспользоваться эргодической гипотезой, то есть заменить временное усреднение (40.7) усреднением по ансамблям возможных углов β и флуктуаций δ v . Таким образом, будем иметь

	~ (δ v)2 sin2 β = (δ v)2 sin2 β ,							(40.8)
I

где черта означает усреднение по ансамблям. Равенство в (40.8) поставлено в предположении, что случайные величины β и δ v статистически независимы. Это допущение естественно, так как угол β задается источником излучения, не связанным с флуктуирующей средой.

Для	вычисления		sin2 β		рассмотрим рис.40.2. Здесь ось
0z − направление, вдоль		которого			распространяется падающее на среду
излучение,	n − единичный вектор,				направленный на точку наблюдения.

Угол между ортами z и n равен θ . Выберем систему координат так, чтобы вектор n лежал в плоскости yz . Тогда вектор E0 , который ортогонален

оси 0z , будет составлять некоторый угол ϕ с осью 0 y . Согласно рис. 40.2, можем записать

p = cos β = sinθ cosϕ ,

где p − проекция вектора n на направление E0 . Следовательно,

sin2 β = 1 − cos2 β = 1 − sin2 θ cos2 ϕ .	(40.9)
В формуле (40.9) угол θ − фиксированная константа, а угол	ϕ есть

случайная величина. Для естественного света ϕ с равной вероятностью принимает любые значения из интервала [0, 2π ]. Поэтому вероятность того, что данный угол лежит в диапазоне dϕ около значения ϕ равна dϕ /(2π ) . Следовательно, по правилу вычисления средних значений

1

2π

sin2 β = 2π ∫0 dϕ (1 − sin2 θ cos2 ϕ ) = 1 − 0.5sin2 θ = 0.5(1 + cos2 θ ) .

64

z

n

θ

β

y

p	ϕ
x	E0
Рис. 40.2
Величина (δ v)2 в (40.8) есть дисперсия	объема v , которая дается

формулой (39.13).

Итак, для средней по времени интенсивности рассеянного света (40.6) находим

			I	= I0
= I			π 2
	0	2λ 4r 2

	π 2 sin2 β (δ v)2													ε			2
											1		−			0		=
		λ	4		r		2							ε
																						(40.10)
													∂v							ε
(1 + cos				2					−kT										−			2
						θ )												1			0	.
																				ε
													∂P T

Выражение (40.10) дает среднюю интенсивность света, рассеянного одним микрообъемом v . Если наблюдать излучение, рассеянное макроскопическим объемом V >> v , удовлетворяющим неравенству

3V << r , то данное излучение будет представляться суммой полей, рассеянных множеством микрообъемов, расположенных внутри объема V . Если флуктуации данных микрообъемов рассматривать как статистически независимые величины, то рассеянные на этих флуктуациях поля будут не когерентны. В результате интенсивность света, рассеянного объемом V , будет равна произведению интенсивности I вида (40.10) на среднее число рассеивающих центров внутри объема V , равное V / v . Еще заметим, в

случае рассеяния света в атмосфере ε / ε0 = n2 ≈ 1, поэтому

	1 −	ε0	= 1 −	1	=	(n −1)(n + 1)	≈ 2(n −1) ,
		ε		n2		n2

где n − показатель преломления атмосферы.

65

При учете сделанных замечаний наблюдаемая интенсивность, рассеянная макроскопическим объемом V атмосферы под углом θ к направлению распространения падающей волны, будет равна

2π 2 (1 + cos2 θ )(n -1)2

kT

¶v

I = I0V

-

.

(40.11)

λ

4

r

2

v

¶P T

Если приближенно рассматривать воздух как идеальный газ, то

Pv = NkT ,

¶v

NkT

v

= -

= -

.

P

2

¶P T

P

Следовательно,

2π 2 (1 + cos2 θ )(n −1)2

= I V

kT

.

(40.12)

I

0

λ 4r 2

P

Важной особенностью формулы (40.12) является резкая зависимость

от длины волны

(

~ 1/ λ 4 ).

Поэтому

днем чистое небо

выглядит

I

I

голубым, а на закате и рассвете –

красным. Отметим также, что согласно

(40.12) интенсивность света, рассеянного вдоль направления распространения падающей волны, вдвое превышает интенсивность света, рассеянного в поперечном направлении. Наконец, при рассмотрении в качестве рассеивающей среды газа Ван-дер-Ваальса следует обратить внимание на резкое возрастание рассеяния вблизи критического состояния, т. е. при (¶P / ¶v)T ® 0 (см. (40.11)). Этот эффект называется критической

опалесценцией.

§ 41. Симметрия кинетических коэффициентов

Важным следствием теории флуктуаций термодинамических параметров является принцип симметрии кинетических коэффициентов, установленный в 1931 г. американским физиком Л. Онсагером.

Для формулировки этого принципа рассмотрим большую замкнутую равновесную систему. Пусть в малых подсистемах, на которые может быть разбита данная система, происходят флуктуации термодинамических параметров. Будем полагать, что в процессе флуктуаций данные подсистемы находятся в состоянии локального термодинамического равновесия в том смысле, как было указано в § 39. Подсистемы в общем случае считаем поливариантными. Состояние каждой из них

характеризуется термодинамическими параметрами a(l ) , где			l − номер
		i
подсистемы, i − номер параметра ( i =		, n ³ 2 ).
	1, n
В силу аддитивности энтропии имеет место равенство
S = ∑Sl (a(l ) ) ,			(41.1)
l

66

где S − энтропия	большой системы, Sl − энтропии	подсистем,
a(l ) − совокупность	термодинамических параметров l − й	подсистемы.

Вследствие флуктуаций, все слагаемые в правой части (41.1) испытывают временные колебания. При этом

			dSl	= ∑ Ji(l ) X i(l )
			dt			i
где	величины	X (l ) = ∂ S			l	∂ a(l )
		i				i

,				(41.2)
и	J (l ) = d a(l )		d t	называют
	i	i

термодинамическими силами и термодинамическими потоками, соответственно.

При отсутствии флуктуаций Ji(l ) = 0 . В этом случае энтропия замкнутой системы максимальна, то есть, в согласии с (41.1) и

определением X i(l ) , X i(l )

= 0 . Предположим, что при малых флуктуациях

параметров a(l )	величины X (l ) и J (l )		связаны линейно:
i	i	i
	Ji(l ) = ∑ L ik(l ) X k(l ) .			(41.3)

k

Здесь детерминированные коэффициенты L ik(l )

, зависящие от температуры,

средней концентрации вещества в подсистеме, напряженности магнитного поля и т. д., называются кинетическими коэффициентами.

Принцип симметрии кинетических коэффициентов Онсагера

утверждает, что если параметры a(l )		являются квадратичными функциями
	i
импульсов частиц, то
L (l )(H) = L (l )(−H) ,			(41.4)
i k	k i

где H − напряженность магнитного поля в системе, созданного внешними источниками.

Для доказательства (41.4) воспользуемся симметрией уравнений механики по отношению к операции отражения времени.

Рассмотрим корреляционную функцию термодинамических параметров l − й подсистемы

ρ (l ) (τ , H) = lim		1	T	a(l ) (t)a(l ) (t + τ )dt .		(41.5)
ik	T →∞ T		∫	i	k
			0
Здесь случайные функции a(l ) (t)			и a(l ) (t)		описывают процессы флуктуаций
	i			k

параметров ai(l ) и ak(l ) , τ − некоторый временной интервал.

Как и в § 38, будем считать, что все величины из совокупности a(l ) являются функциями координат q j и импульсов p j всех N частиц

большой замкнутой системы. Кроме этого предположим, что от импульсов эти величины зависят квадратично. Тогда выражение (41.5) может быть записано в форме

67

ρ (l ) (τ , H) = lim		1	T	a(l )[q	(t), p2	(t)]a(l )
ik	T ®¥ T		∫	i j	j	k
			0

[q	j	(t + τ ), p2	(t + τ )]dt .	(41.6)
		j

Здесь координаты и импульсы частиц удовлетворяют уравнениям Гамильтона (23.1), в которых гамильтониан, учитывающий силу Лоренца, имеет вид

	N	1	(pl	− el μ 0 Al )2 + U (q1,...,qN ) ,
	H = ∑				(41.7)
	l =1	2m
		l
где Al ,	ql , pl , ml и el − векторный магнитный потенциал, радиус-вектор,
вектор	импульса,	масса		и заряд l − й частицы,	μ 0− магнитная

проницаемость вакуума, U − потенциальная энергия системы без учета ее взаимодействия с магнитным полем. В пренебрежении запаздыванием электромагнитного взаимодействия между частицами

	A i = A(q i ) + 4π ∑		el pl	,	(41.8)
			q i − q l
	l ¹i ml
где A(r) − векторный потенциал магнитного поля напряженности
	H = Ñ × A ,				(41.9)
создаваемого в системе внешними источниками.
Поскольку большая замкнутая система равновесна, случайные
процессы a(l ) (t)	и a(l ) (t) являются стационарными. В этом случае начало
i	k

отсчета времени в (41.6) произвольно. Это означает, что значение интеграла в правой части (41.6) не зависит от начальных условий для уравнений Гамильтона.

Перейдем в (41.6) к новым переменным qi′ , pi′ , t′ на основании соотношений

qi′(t′) = qi (t),

pi′(t′) = − pi (t), t′ = T − t ,

(41.10)

где i =

. Тогда

1, 3N

ρik(l ) (τ , H) = lim

1

T

ai(l )[q′j (t′), p′j2

(t′)]ak(l )[q′j (t′ −τ ), p′j2 (t′ −τ )]dt′ .

(41.11)

∫

T ®¥ T

0

Согласно (41.10),

dqi′

dqi′

dqi

dpi′

dpi′

dpi

= −

=

,

= −

= −

.

dt

dt′

dt

dt

dt′

dt

В соответствии с (23.1) и (41.10)

dqi′

∂H

dpi′

∂H

=

∂pi′

,

= −

∂qi′ ,

(41.12)

dt′

dt′

где гамильтониан определен формулой (41.7), в которой выполнены замены pl → − pl′ , ql → ql′ .

С точностью до обозначений канонических переменных и времени уравнения (41.12) совпадают с исходными уравнениями Гамильтона (23.1).

68

Однако гамильтониан в (41.12) отличается от гамильтониана (41.7) знаком перед первым слагаемым в правой части выражения (41.8). Это, очевидно, означает, что величинам q′j и p′j можно придать смысл координат и

импульсов частиц рассматриваемой системы при условии, что данная система находится в магнитном поле, напряженность которого в каждой точке пространства отличается знаком от напряженности (41.9). Следовательно, в соответствии с определением (41.6), правую часть в выражении (41.11) можно рассматривать как корреляционную функцию

ρ (l ) (−τ , −H) . Тогда из (41.11) будет следовать, что
ik
ρ (l ) (τ , H) = ρ (l ) (−τ , −H) .		(41.13)
ik	ik
Заметим, что начальные условия для уравнений (23.1) и (41.12)
различны, ибо согласно (41.10)	qi′(0) = qi (T ), pi′(0) = − pi (T ) . Но,	как уже

отмечалось, корреляционная функция (41.6) не зависит от начальных условий для канонических переменных, что оправдывает запись (41.13).

Перейдем в определении (41.5) к новой переменной интегрирования x = t −τ . Тогда для правой части выражения (41.13) получим

	ρ (l ) (−τ , −H) = lim			1	T −τ	a(l ) (x + τ )a(l ) (x)dx .				(41.14)
		ik	T →∞ T ∫			i	k
					−τ
Из	(41.5) и	(41.14)	следует,				что при	любом	конечном τ
ρ (l ) (−τ , −H) = ρ		(l ) (τ , −H) .	Поэтому				выражение	(41.13)	может	быть
i k	k i
представлено также в форме
		ρ (l ) (τ , H) = ρ				(l )	(τ , −H) .			(41.15)
		i k				k i
	Проанализируем левую часть (41.15), предполагая, что									τ → 0 .
Согласно (41.5) имеем

							ρ (l ) (τ , H) =
							ik
	где
			= lim	1	T
		a(l )a(l )				a(l ) (t)a(l ) (t)dt
		i k	T →∞ T		∫	i	k
					0

	ai(l )ak(l ) + γ i(kl )τ ,
	(l )	1			T	(l )		dak(l ) (t)
, γ ik		= lim			∫	ai	(t)		dt .
		T →∞ T						dt
					0

Учитывая (41.1) и (41.3), можем записать

γ (l ) =	∑	L (l )	(H) lim	1	T	a(l ) (t) ∂S (t) dt .
					∫
i k		k j	T →∞ T			i	∂a(l )
	j				0		j
Случайные величины			a(l ) и ∂ S / ∂ a(l )				в (41.16)
			i			j

(41.16)

рассматриваются в

один и тот же момент времени. Поэтому, предполагая процесс флуктуаций стационарным и эргодическим, заменим временное усреднение в (41.16) усреднением по ансамблю возможных значений всех термодинамических параметров рассматриваемой подсистемы. Вероятность для данных параметров дается выражением (38.8). Следовательно,

69

(l )	(l )	(l )	(l )	(l )	(l ) ∂S			S (a1(l ) , a2(l ) ,..., an(l ) )
γ i k	= C∑ L k j	(H)∫ da1	∫da2	...∫dan	ai		exp			. (41.17)
						(l )		k
	j					∂ a j

Выполним в (41.17) интегрирование по частям по переменной a(l ) и

j

предположим,

что плотность вероятности C exp(S / k )

обращается в нуль

на краях промежутков интегрирования в (41.17). В результате

(l )

(l )

(l )

(l )

(l ) ∂ ai(l )

S (a1(l ) , a2(l ) ,..., an(l ) )

γ i k

= −k C∑ L k j

(H)∫ da1

∫ da2

... ∫dan

(l ) exp

. (41.18)

k

j

∂ a j

Учитывая определение нормировочной постоянной C (38.9), а также то,

что

∂ a(l ) / ∂ a(l )

= δ

i j

(δ

i j

− символ

Кронекера), из

(41.18)

находим:

i

j

γ (l )

= −k L (l )(H) . Следовательно, при τ → 0

i k

k i

ρ (l ) (τ , H) =

− kτ L (l )

a(l )a(l )

(H) .

(41.19)

ik

i k

k i

Совершенно аналогично может быть доказано соотношение

ρk(li) (τ , −H) = ak(l )ai(l ) − kτ L i(lk)

(−H) . (41.20)

Нетрудно видеть, что принцип симметрии кинетических коэффициентов (41.4) является прямым следствием формул (41.15), (41.19)

и (41.20).

Необходимо отметить, что соотношения (41.1) – (41.3) имеют место не только при флуктуациях, но и при протекании в системе детерминированных процессов переноса тепла, массы, либо заряда. Поскольку при выводе принципа (41.4) не использовались какие-либо специфические допущения о механизмах, вызывающих изменения

параметров a(l ) , этот принцип остается в силе и в случае указанных процессов. В качестве примера рассмотрим процесс переноса заряда в анизотропной среде.

Пусть в проводящем монокристалле присутствует электрическое поле напряженности E . Как известно из электродинамики, это поле вызывает ток плотности j с компонентами

3
ji = ∑σ i k Ek (i =
	1,3) ,		(41.21)
k =1
где σ − тензор проводимости проводника.
Рассмотрим в качестве l − ой термодинамической			подсистемы

некоторый малый параллелепипед фиксированного объема dV , одна из граней которого перпендикулярна вектору j. Эта подсистема может быть

охарактеризована макроскопическими параметрами

	a	(l )= ρ r dV		( i =	1,3	),	(41.22)
		i	i
где ri есть	i − я компонента			радиус-вектора			r центра объема dV ,
ρ − средняя	плотность		подвижных носителей				заряда в данном объеме.

70