
- •Замечательные точки в треугольнике .
- •Средняя линия в треугольнике и ее свойства. Теорема Вариньона. Площади. [7,8,9].
- •Подсчет углов. Вписанный угол. Угол между хордами и секущими к окружности. Угол между касательной и хордой. [7,8,9].
- •Вписанный четырехугольник. Критерии вписанного четырехугольника (5 признаков). [7,8,9]
- •Теорема о касательной и секущей. [7,8,9]
- •Теорема Фалеса с доказательством. Теорема о пропорциональных отрезках. [7,8,9]
- •Лемма Мансиона и ее обобщение. [7,8,9]
- •Окружность Эйлера 9 точек. [7,8,9]
- •Прямая Симпсона. [7,8,9]
- •Теорема Птолемея. [7,8,9,10]
- •Теорема Чевы и ее обобщение. Обратная теорема Чевы. [7,8,9]
- •Теорема Менелая и ее обобщение. Обратная теорема Менелая. [7,8,9]
- •Тригонометрическая форма теоремы Чевы. Изотомическое и изогональное сопряжение. Доказать, что точки и изогонально сопряжены. Точка Лемуана. [7,8,9,12]
- •Гомотетия, свойства гомотетии. Теорема Эйлера о том, что точки лежат на одной прямой, причем . [7,8,9]
- •Вневписанные окружности. Точка Нагеля . Свойства нагелиан. Доказать, что точки и изотомически сопряжены. [7,8,9]
- •Теорема Архимеда о двух касающихся окружностях. Задача Архимеда о ломаной.[5,12]
- •Теорема о прямой Эйлера-Нагеля. Доказать, что , .[5]
- •Степень точки относительно окружности. Радикальная ось двух окружностей. Радикальный центр трех окружностей.[4,5,7,8,9]
- •Формула Эйлера для вычисления расстояния между центрами вписанной и описанной окружности. [7,8,9]
- •Точка Торричелли и ее свойства.[3,4,5]
- •Треугольник наименьшего периметра, вписанный в данный треугольник. [3,4,5]
- •Теорема Брианшона. [3,4,5,7,8]
- •Окружность, вписанная в сегмент и ее свойства.[5]
- •Лемма о бабочке.[10, задача 122]
- •Понятие центра масс системы материальных точек. Существование, единственность, группировка с доказательством. Теорема о центроиде четырехугольника.[1,2,5,12]
- •Доказать с помощью понятия центра масс, что медианы (биссектрисы, высоты) пересекаются в одной точке и найти пропорцию, в которой точка пересечения делит соответствующую линию. [1,2,5,12]
- •Понятие барицентрических координат точки относительно треугольника . Найти барицентрические координаты точек: середины , центров вневписанных окружностей. [1,2,5,12]
- •Условие принадлежности одной прямой трех точек с заданными барицентрическими координатами. Уравнение прямой линии в барицентрических координатах. [1,2,5,12]
- •Признак ромба: если радиусы окружностей, вписанных в треугольники, образуемые сторонами и диагоналями четырехугольника, равны, то этот четырехугольник – ромб.
- •Теорема о биссектрисах внешних углов полного четырехугольника.
- •Теорема о трех центрах гомотетий (о трех колпаках).[7]
- •Инверсия относительно окружности. Деление отрезка пополам с помощью одного циркуля. Стереографическая проекция.[7]
- •Полярное соответствие. Свойство взаимности поляр. Двойственность в геометрии. Теорема Паскаля. [7]
- •Векторы и комплексные числа.
- •Разное.
- •Литература по курсу элементарная математика (геометрия)
-
Признак ромба: если радиусы окружностей, вписанных в треугольники, образуемые сторонами и диагоналями четырехугольника, равны, то этот четырехугольник – ромб.
-
Пусть
 - точка пересечения диагоналей выпуклого
четырехугольника
- точка пересечения диагоналей выпуклого
четырехугольника
 .
Известно, что радиусы вписанных
окружностей треугольников
.
Известно, что радиусы вписанных
окружностей треугольников
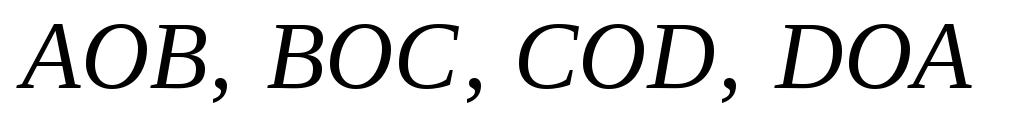 равны.
Доказать, что
равны.
Доказать, что
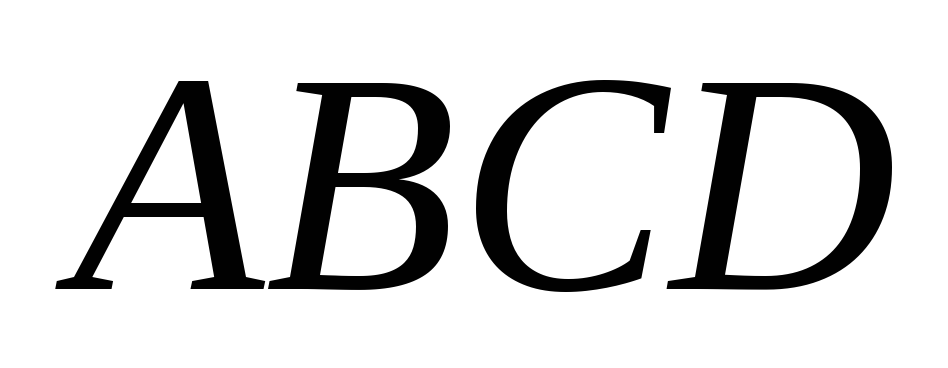 - ромб.
- ромб.
Решение. Пусть, скажем,
![]() .
В этом случае при центральной симметрии
относительно точки
.
В этом случае при центральной симметрии
относительно точки
![]() образ треугольника
образ треугольника
![]() будет лежать внутри треугольника
будет лежать внутри треугольника
![]() ,
и, следовательно, радиус вписанной
окружности треугольника
,
и, следовательно, радиус вписанной
окружности треугольника
![]() будет меньше радиуса вписанной окружности
треугольника
будет меньше радиуса вписанной окружности
треугольника
![]() .
В случае же
.
В случае же
![]() из
равенства площадей треугольников
из
равенства площадей треугольников
![]() получаем,
что
получаем,
что![]() - ромб.
- ромб.
-
Теорема о биссектрисах внешних углов полного четырехугольника.
1.
-
Теорема о трех центрах гомотетий (о трех колпаках).[7]
1.
-
Инверсия относительно окружности. Деление отрезка пополам с помощью одного циркуля. Стереографическая проекция.[7]
-
Пусть дана окружность
 с центром
с центром
 и радиусом
и радиусом
 .
Инверсией относительно окружности
.
Инверсией относительно окружности
 называют преобразование, переводящее
произвольную точку
называют преобразование, переводящее
произвольную точку
 ,
отличную от
,
отличную от
 ,
в точку
,
в точку
 ,
лежащую на луче
,
лежащую на луче
 ,
причем
,
причем
 .
Окружность
.
Окружность
 в этом случае называется окружностью
инверсии.
в этом случае называется окружностью
инверсии.
Пусть при инверсии относительно
окружности
![]() точка
точка
![]() переходит в точку
переходит в точку
![]() ,
точка
,
точка
![]() - в
- в
![]() .
Докажите, что треугольники
.
Докажите, что треугольники
![]() и
и
![]() подобны.
подобны.
-
Постройте с помощью одного циркуля:
-
отрезок, который в два раза длиннее данного отрезка;
-
отрезок, который в
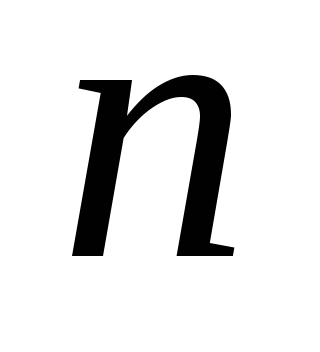 раз длиннее данного отрезка;
раз длиннее данного отрезка; -
середину данного отрезка;
-
отрезок в
 раз меньший данного отрезка;
раз меньший данного отрезка; -
инверсный образ данной точки
 относительно окружности
относительно окружности
 .
.
-
-
В сегмент, образованный дугой окружности и хордой, вписываются всевозможные пары касающихся окружностей.
-
Найти множество их точек касания.
-
Для каждой пары касающихся окружностей через точку касания проводится общая касательная. Доказать, что все построенные прямые проходят через одну точку.
-
-
На биссектрисе угла
 треугольника
треугольника
 внутри треугольника взяты точки
внутри треугольника взяты точки
 и
и
 так, что
так, что
 .
Докажите, что:
.
Докажите, что:
a)
![]() ;
;
b) окружность, проходящая
через точки
![]() ,
,
![]() и касающаяся отрезка
и касающаяся отрезка
![]() ,
касается окружности описанной около
треугольника
,
касается окружности описанной около
треугольника
![]() .
.
-
Полярное соответствие. Свойство взаимности поляр. Двойственность в геометрии. Теорема Паскаля. [7]
-
Пусть дана окружность
 с центром в точке
с центром в точке
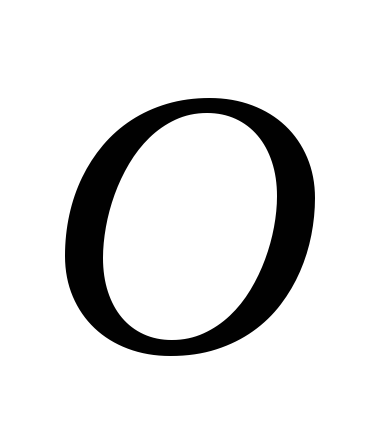 и радиусом
и радиусом
 .
Полярой точки
.
Полярой точки
 ,
не совпадающей с центром окружности,
называется множество точек
,
не совпадающей с центром окружности,
называется множество точек
 в плоскости окружности, для которых
в плоскости окружности, для которых
 .
Доказать, что поляра точки
.
Доказать, что поляра точки
 - это прямая, перпендикулярная прямой
- это прямая, перпендикулярная прямой
 .
Что является полярой точки, лежащей
на окружности?
.
Что является полярой точки, лежащей
на окружности? -
Точка
 называется полюсом прямой
называется полюсом прямой
 ,
которая является полярой точки
,
которая является полярой точки
 .
Мы будет обозначать поляру
.
Мы будет обозначать поляру
 и полюс
и полюс
 .
Что является полюсом касательной к
окружности
.
Что является полюсом касательной к
окружности
 ?
Доказать, что отображение
?
Доказать, что отображение
 является взаимно однозначным соответствием
между множеством точек на плоскости,
отличных от центра
является взаимно однозначным соответствием
между множеством точек на плоскости,
отличных от центра
 окружности
окружности
 ,
и множеством прямых на плоскости, не
проходящих через центр
,
и множеством прямых на плоскости, не
проходящих через центр
 .
. -
Доказать свойство взаимности поляр:
 .
. -
Доказать, что центр
 лежит на прямой
лежит на прямой
 тогда и только тогда, когда
тогда и только тогда, когда
 .
. -
Пусть
 - описанный четырехугольник,
- описанный четырехугольник,
 точки касания вписанной окружности со
сторонами
точки касания вписанной окружности со
сторонами
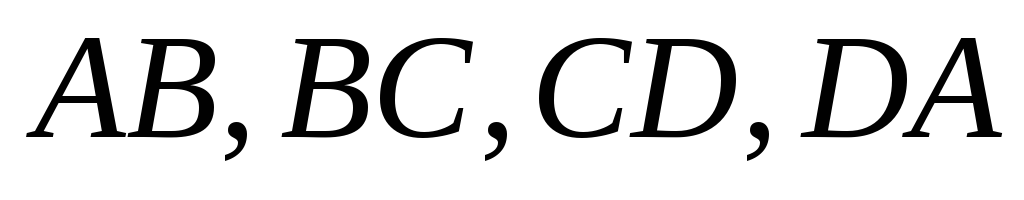 ,
соответственно. Докажите, что либо
точка пересечения прямых
,
соответственно. Докажите, что либо
точка пересечения прямых
 и
и
 лежит на прямой
лежит на прямой
 ,
либо прямые
,
либо прямые
 и
и
 параллельны
параллельны
 .
. -
(Теорема Паскаля) Пусть
 -
вписанный шестиугольник. Доказать, что
точки пересечения пар противоположных
сторон этого шестиугольника (если они
существуют) лежат на одной прямой.
Указание. Примените полярное
преобразование относительно описанной
окружности и воспользуйтесь теоремой
Брианшона.
-
вписанный шестиугольник. Доказать, что
точки пересечения пар противоположных
сторон этого шестиугольника (если они
существуют) лежат на одной прямой.
Указание. Примените полярное
преобразование относительно описанной
окружности и воспользуйтесь теоремой
Брианшона. -
В треугольнике
 на сторонах
на сторонах
 и
и
 взяты точки соответственно,
взяты точки соответственно,
 и
и
 пересекаются в точке
пересекаются в точке
 .
Оказалось, что четырехугольник
.
Оказалось, что четырехугольник
 - описанный с центром вписанной окружности
- описанный с центром вписанной окружности
 .
Пусть
.
Пусть
 - основание перпендикуляра из точки
- основание перпендикуляра из точки
 на прямую
на прямую
 .
Докажите, что
.
Докажите, что
 - биссектриса
- биссектриса
 .
.
-
Лемма о шестиугольнике, вписанном в окружность.[7]
-
Пусть
 - стороны шестиугольника, вписанного
в окружность. Доказать, что большие
диагонали этого шестиугольника
пересекаются в одной точке тогда и
только тогда, когда
- стороны шестиугольника, вписанного
в окружность. Доказать, что большие
диагонали этого шестиугольника
пересекаются в одной точке тогда и
только тогда, когда
 .
.
-
Сформулируйте и докажите лемму о шестиугольнике для случая самопересекающегося шестиугольника.
-
Построение поляры точки с помощью одной линейки. Построение касательной к окружности с помощью одной линейки.[7]
1.
-
Автополярный треугольник.[7]
1. Треугольник
![]() называется автополярным относительно
окружности
называется автополярным относительно
окружности
![]() ,
если каждая сторона треугольника
(прямая, содержащая сторону) является
полярой противоположной вершины
относительно
,
если каждая сторона треугольника
(прямая, содержащая сторону) является
полярой противоположной вершины
относительно
![]() .
Доказать, что автополярный треугольник
является тупоугольным.
.
Доказать, что автополярный треугольник
является тупоугольным.
44. Неравенства в геометрии.
-
Д
 аны
три окружности
аны
три окружности
 ,
,
 ,
,
 соответственно с центрами
соответственно с центрами
 ,
которые пересекаются в одной точке.
Кроме того, окружность
,
которые пересекаются в одной точке.
Кроме того, окружность
 пересекается с
пересекается с
 также в точке А,
также в точке А,
 с
с
 в точке C,
в точке C,
 с
с
 в точке B. Пусть Х – точка
на окружности
в точке B. Пусть Х – точка
на окружности
 и прямая АХ пересекает
и прямая АХ пересекает
 в точке
в точке
 ,
а прямая XB пересекает
,
а прямая XB пересекает
 в точке
в точке
 (см. рисунок). Доказать, неравенство
для площадей треугольников
(см. рисунок). Доказать, неравенство
для площадей треугольников
 .
Решение. Заметим, во-первых, что
точки
.
Решение. Заметим, во-первых, что
точки
 лежат
на одной прямой. В самом деле,
лежат
на одной прямой. В самом деле,
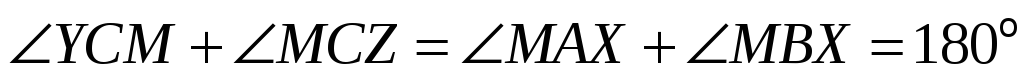 .
Треугольник
.
Треугольник
 подобен треугольнику
подобен треугольнику
 с
коэффициентом
с
коэффициентом
 .
С этим же коэффициентом подобны
треугольники
.
С этим же коэффициентом подобны
треугольники
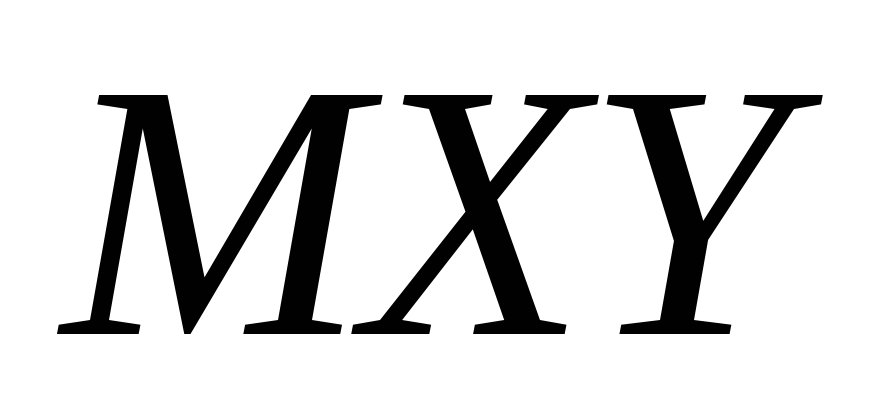 и
и
 .
То есть
.
То есть
 .
Отсюда вытекает неравенство для площадей
.
Отсюда вытекает неравенство для площадей
 .
. -
Доказать, что произведение длин любых двух сторон треугольника не меньше, чем произведение диаметров окружностей вписанной и описанной около треугольника. Решение. Пусть
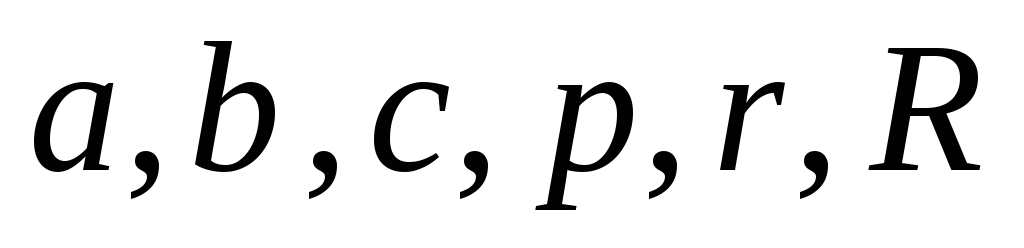 - стороны, полупериметр, радиусы вписанной
и описанной окружности треугольника,
соответственно. Нужно доказать
неравенство:
- стороны, полупериметр, радиусы вписанной
и описанной окружности треугольника,
соответственно. Нужно доказать
неравенство:
 .
Кроме того, площадь треугольника может
быть вычислена по формулам:
.
Кроме того, площадь треугольника может
быть вычислена по формулам:
 .
Поэтому требуемое неравенство
преобразуется к виду:
.
Поэтому требуемое неравенство
преобразуется к виду:
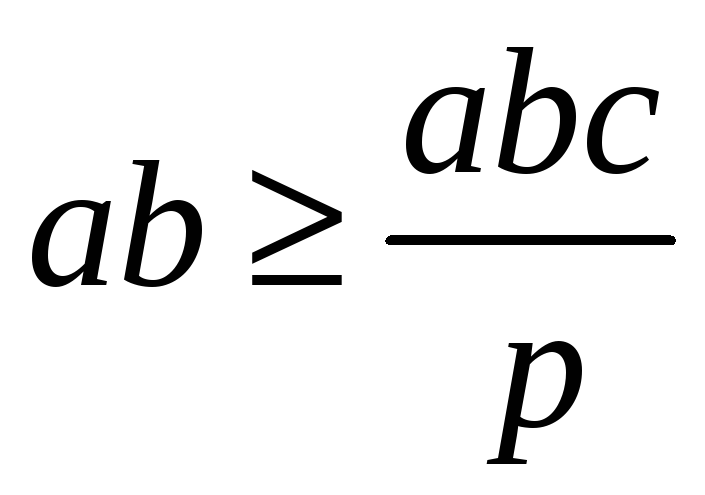 ,
что очевидно.
,
что очевидно. -
Продолжения медиан
 треугольника
треугольника
 пересекают описанную около него
окружность в точках
пересекают описанную около него
окружность в точках
 соответственно. Доказать, что
соответственно. Доказать, что
 .
. -
Среди всех тетраэдров, вписанных в данный правильный тетраэдр, найти тетраэдр с наименьшей суммой ребер. (Вершины вписанного тетраэдра лежат на различных гранях данного тетраэдра).
-
Внутри остроугольного треугольника
 с максимальной стороной
с максимальной стороной
 взята точка
взята точка
 так, что
так, что
 - прямой. Из точки
- прямой. Из точки
 опущены перпендикуляры
опущены перпендикуляры
 и
и
 на стороны
на стороны
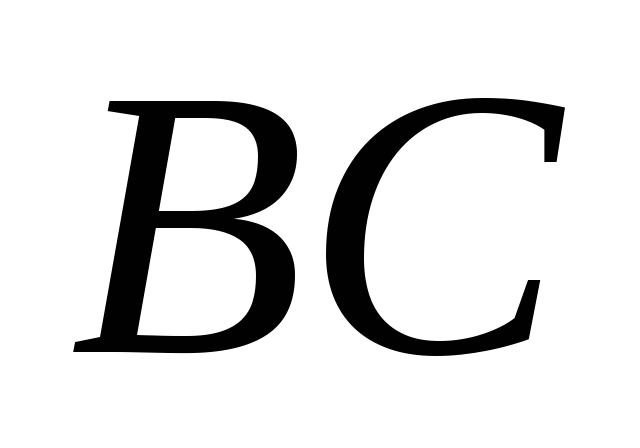 и
и
 .
Прямая
.
Прямая
 пересекает сторону
пересекает сторону
 в точке
в точке
 .
Докажите, что периметр
.
Докажите, что периметр
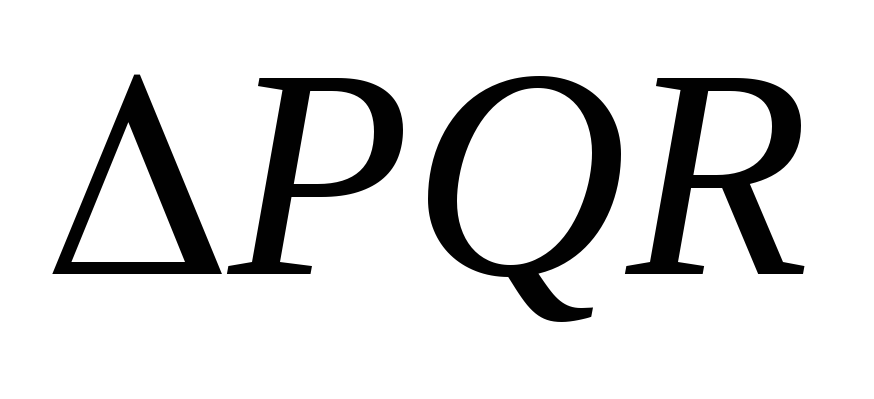 меньше
меньше
 .
.
-
Существует ли выпуклый многоугольник, у которого каждая сторона равна какой-то диагонали, а каждая диагональ равна какой-то стороне?
-
