Осуществляется нумерация ребер графа.
						Записывается n-1 множеств номеров ребер,
				инцидентных n-1 вершинам графа (кроме одной
				из		n	вершин): Ω1 = {1,3,5}, Ω2 = {1,2,4}, Ω3 =
1	4		2	{2,3,6}. Образуется				таблица, столбцы	которой
				представляют собой				все возможные	сочетания
			6
5				элементов множеств Ω1, Ω2, Ω3:
		3		éW		ù	é1 1 1 1 1 3 3 3 3 3 5 5 5 5 5 5 5 5ù
				ê	1	ú	ê		ú
	Рис. 2.25			êW2 ú			= ê2 2 4 4 4 1 1 2 4 4 1 1 1 2 2 4 4 4ú.
				êW	3	ú	ê3 6 2 3 6 2 6 6 2 6 2 3 6 3 6 2 3 6ú
				ë		û	ë		û

4. Столбцы, содержащие одинаковые ребра, попарно вычеркиваются независимо от их порядка (первый и шестой столбцы). Каждый столбец оставшейся таблицы соответствует ребрам одного из покрывающих деревьев.

Экстремальное дерево графа– это покрывающее дерево, связывающее его вершины наиболее экономичным образом(линии связи, автомобильные дороги и т. д.). Задача построения экстремального дерева формируется следующим образом. Каждому ребру xixj полного графа с n вершинами приписывается вес qij, численно выражающий длину, стоимость или другую величину, характеризующую любую пару вершин. Требуется построить экстремальное дерево, связывающее все вершины так, чтобы был минимальным суммарный вес всех ветвей дерева åqij ®min. Способ построения экстремального дерева

основан на последовательном введении в него ребер с приоритетом по минимуму их весов. Сначала для дерева выбирается ребро с наименьшим весом. Затем на каждом следующем шаге рассматривается минимальное по весу ребро и, если оно не образует цикла с ранее выбранными ветвями, вводится в дерево. Построение заканчивается после отбора для дерева n-1 ребер.

2.10. Корневые деревья. Код дерева

Любое дерево можно рассматривать как корневое, если одну из вершин выбрать в качестве корня, а остальные расположить на соответствующих уровнях (ярусах).

Пример корневого дерева приведен на рис. 2.26.

Корень располагается на нулевом уровне. Припишем каждой вершине некоторое число, называемое весом. Веса концевых вершин равны единице, вес корня дерева равен числу всех его вершин. Вес произвольной вершины равен общему числу вершин поддерева, корнем которого она является. Возле каждой вершины дерева на рис. 2.26 указан ее вес.

При таком представлении корневое дерево однозначно определяется упорядоченной последовательностью β(G) весов его вершин, в которой на первом

40

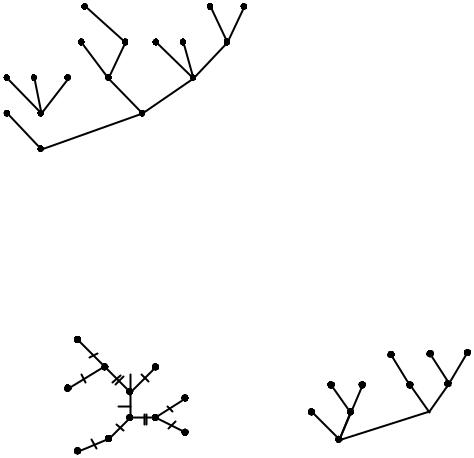
месте стоит вес корня дерева, а затем следуют соответствующие последова-

тельности для поддеревьев: β(G) = (17, 1, 4, 1, 1, 1, 11, 4, 1, 2, 1, 6, 1, 1, 3, 1, 1).

4					1		1 1		Одна из стандартных проце-
								дур	выбора	корня состоит в сле-
					1	2 1	1
3								дующем: из дерева удаляются все
	1		1		1		3	концевые вершины и ребра, затем
2								в полученном дереве снова удаля-
					4		6
	1							ются все вершины и ребра. В пер-
1
					4	11		вом	случае	оставшаяся	вершина
0								выбирается в качестве корня и
			17		Рис. 2.26			называется		центром, во	втором
								случае две вершины и связываю-
								щее их ребро образуют бицентр.
	При этом за корень принимается та вершина, из которой вырастает дерево

с меньшим числом вершин (если число вершин одинаково, то за корень принимается любая из вершин бицентра).

	На рис. 2.27, а приведено дерево,	в котором выделен бицентр, корневая
	форма этого дерева изображена на рис. 2.27, б.
	корень	3
	бицентр	2
		1
		0
	а		б

Рис. 2.27

Аналитически корневое дерево можно задать также с помощью кода γ(G), представляющего собой последовательность 0 и 1, записанную в определенном порядке. Осуществляется обход дерева по всем ребрам по одному разу в каждом из противоположных направлений. При движении по ребру от корневой вершины в последовательность g(G) записывается 0, а при обратном движении – 1. Обход начинается и заканчивается в корне дерева. Длина последовательности g(G) равна удвоенному количеству ребер дерева. Для графа, приведенного на рис. 2.27, б, g(G) = (01001011000110010111).

41