В соответствии с изменением амплитуды изменяется и средняя за период высокой частоты мощность модулированного сигнала, которая пропорциональна среднему квадрату амплитуды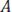

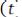
Произведено усреднение по времени. Эта мощность в (1+0,5m2) раз превышает мощность несущего сигнала. При 100% модуляции средняя

мощность составит 1,5P0 , где 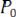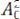– мощность несущего сигнала.

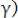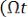
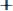
Среднее значение за период модулирующей функции равно нулю, с среднее значение 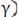равно 0,5.

При передаче дискретных сообщений модулированный сигнал имеет вид, показанный на рис. 6.29.

S (t)					t

T

a (t )

Рис. 6.29

Такие сигналы называются радиоимпульсами. Фазы высокочастотного заполнения от импульса к импульсу не изменяются.

6.10. Частотный спектр АМ сигнала

Установим связь между спектром АМ сигнала и спектром модулирующей функции S(t). Подставим (6.24) в (6.23), тогда

Первое слагаемое в (6.25) – это исходный высокочастотный немодулированный сигнал с частотой 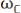. Второе слагаемое, являющееся продуктом модуляции, можно представить в виде суммы

121

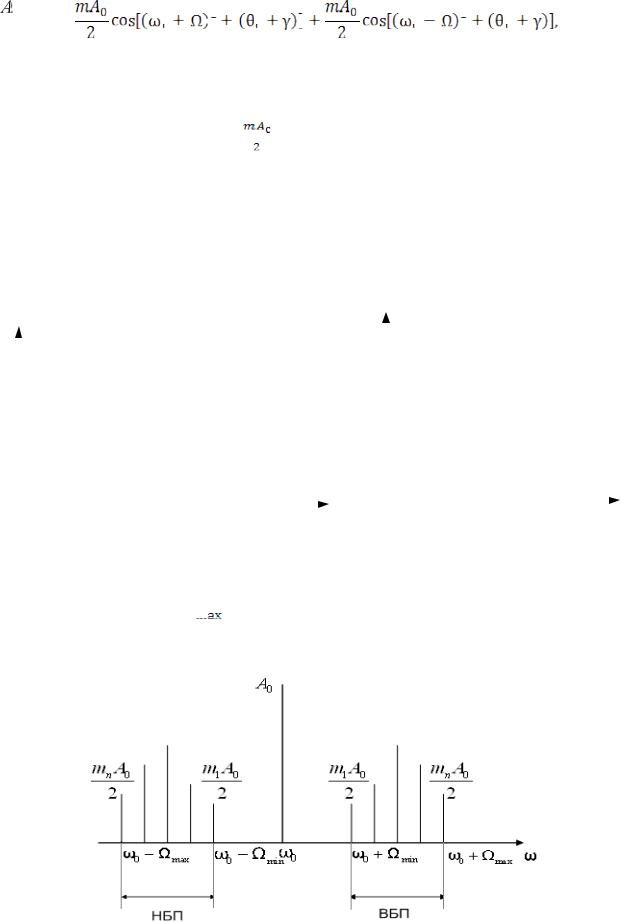
где слагаемые соответствуют новым гармоническим колебаниям, появляющимся в процессе модуляции амплитуды.

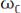
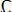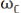
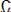Частоты и называют верхней и нижней боковыми часто-

тами модуляции. Амплитуды		этих колебаний одинаковы, а их фазы сим-

метричны относительно фазы несущего сигнала. Спектр показан на рис. 6.30. Ширина спектра равна удвоенной частоте модуляции 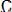, а амплитуды не превышают половины амплитуды .

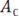Аналогичные результаты можно получить при модуляции любым сложным сигналом.

Пусть модулирующая функция 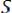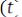имеет спектр, представленный на рис. 6.31.

S(Ω)

S3

mA

mA0

S2

Sn

S1

0

2

2

Ωmin	Ωmax	Ω
Рис. 6.30	Рис. 6.31

Здесь 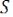– амплитуды гармонических составляющих, входящих в спектр сигнала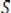 ; и 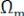– граничные частоты спектра. Для определения спектра АМ сигнала достаточно сместить на 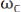спектр огибающей амплитуд, как показано на рис. 6.32.

Рис. 6.32

122

Спектр сигнала содержит кроме основной составляющей верхнюю и нижнюю боковые полосы частот(ВБП и НБП). Коэффициенты модуляции , , 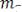…, 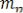пропорциональны амплитудам 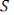, , 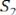…, 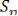соответствующих гармоник, входящих в состав функции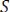 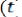. Ширина спектра определяется величиной .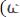

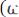
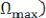
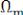6.11. Основные вероятностные характеристики случайных сигналов

Случайными называются сигналы, значения которых не могут быть предсказаны с вероятностью единица в каждый момент времени. Это могут быть различные помехи и возмущения, такие как колебания параметров источников питания, шумы элементов устройств, внешние помехи и т. д. Будем рассматривать случайные сигналы, как случайные функции времени 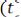. Их называют стохастическими процессами.

Существует ряд вероятностных характеристик, по которым можно отличить один случайный процесс от другого.

1. Математическое ожидание (первый момент М) случайного процесса это неслучайная функция, определяемая выражением

где	– закон распределения случайного процесса.
	Кривая	является некоторой средней кривой, относительно которой

колеблются значения случайной функции. Математическое ожидание служит теоретической оценкой среднего по множеству значения случайной величины, которое определяется на основании множества наблюдений над множеством однотипных систем, находящихся в одинаковых условиях.

2. Дисперсия случайной функции Dx определяется выражением

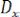
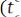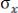
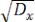
Это неслучайная функция, равная математическому ожиданию от квадрата отклонения случайной функции от её среднего значения. – усреднённая мера отклонения случайной функции от её математического ожидания. Дисперсия определяет полосу рассеяния для реализации случайной функции. Величина 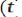носит название среднеквадратического отклонения.

Случайные процессы делят настационарные и нестационарные. Случайный процесс называется стационарным, если его вероятностные характеристики не изменяются во времени. Математическое ожидание и дисперсия стационарного случайного процесса равны постоянным величинам.

Встречающиеся в большинстве практических задач случайные функции имеют нормальный или Гауссов закон распределения, для которого

123

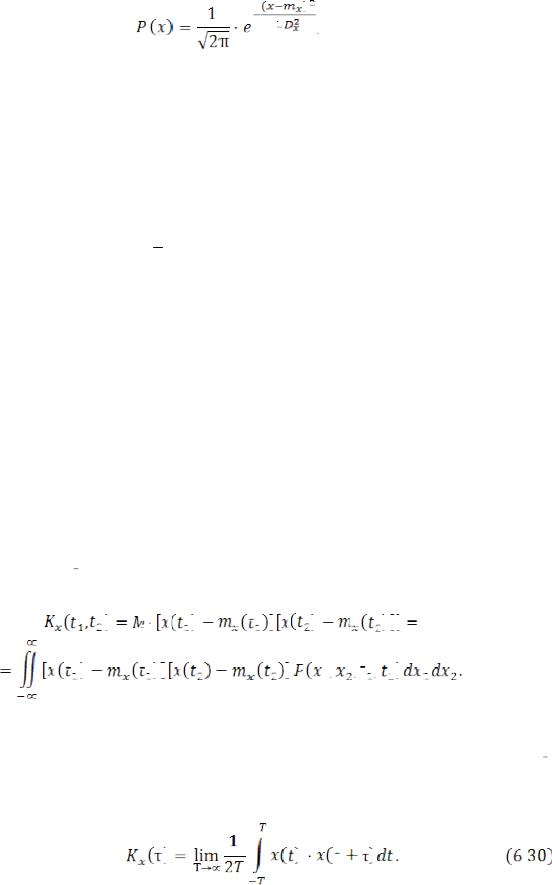
(6.28)

где 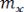– математическое ожидание; 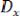– дисперсия случайной функции. Математическое ожидание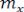 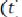было определено как среднее по мно-

жеству значение случайной функции .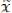

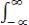
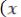
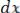Существует также понятие среднего по времени значения случайной функции. Оно определяется на основании наблюдения за одной и той же системой на протяжении достаточно длительного времени Т. Эти средние обозначаются прямой чертой и определяются выражением:

				1	T
	x	=	lim		ò x(t)dt .
			T ®¥ 2T		-T

Вообще величины средние по множеству и по времени различны, но существуют случайные процессы, для которых доказана эргодическая теорема:

Любая статистическая характеристика, полученная усреднением по множеству с вероятностью сколь угодно близкой к единице, совпадает с характеристикой, усреднённой по времени.

Эта теорема доказана не для всех стационарных процессов, однако её применяют к большинству стационарных процессов с нормальным или гауссовым законом распределения.

3. Корреляционные функции случайных процессов. Корреляционная функция характеризует степень взаимосвязи значений случайной функции в различные моменты времени. Корреляционная функция связывает между собой отклонения случайной функции от её математического ожидания при двух значениях аргумента и 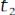и равна математическому ожиданию произведения этих отклонений.

(6.29)

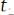
Корреляционная функция стационарного случайного процесса зависит только от одной переменной– разности двух моментов времени. Формула (6.29) определена на основании понятия среднего по множеству. В соответствии с эргодической теоремой корреляционная функция может быть определена как среднее по времени

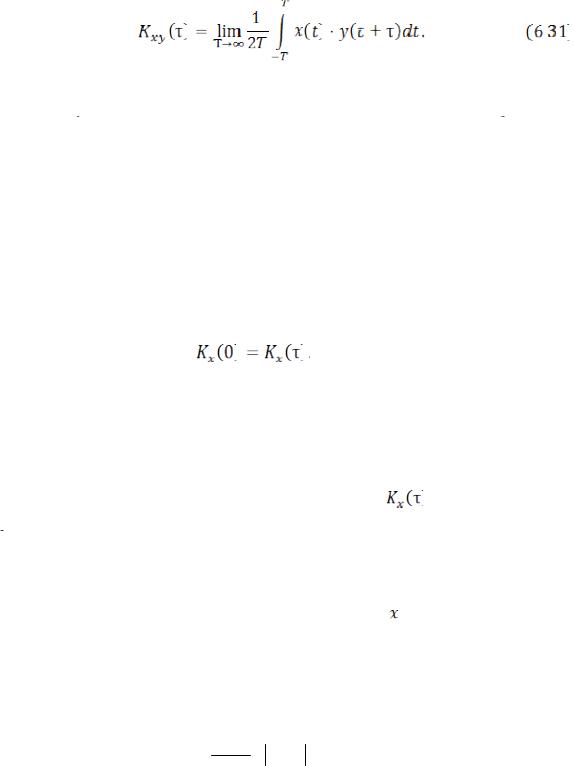
Это выражение используется наиболее часто. Для оценки связи двух случайных процессов 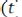и 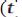вводится взаимная корреляционная функция

124

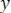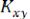
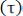
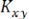
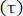
Для статистически независимых процессовx и взаимно-корреляци- онная функция . Однако обратный вывод о том, что если 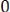, то процессы независимы, справедлив лишь в отдельных случаях, например для процессов с нормальным законом распределения. Общей силы обратный вывод не имеет.

Основные свойства автокорреляционных функций

1. Автокорреляционная функция

		1	T
Kx (t) =	lim		ò x(t) × x(t + t)dt
	T ®¥ 2T		-T

является убывающей функцией, значение которой при любом не может превышать её начального значения.

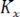
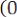
2. Начальное значение автокорреляционной функции равно дисперсии случайного процесса 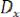и характеризует мощность флуктуационной составляющей эргодического процесса.

3.Автокорреляционная функция является чётной, т. е. .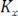

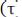
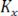
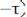4.Типичная корреляционная функция стационарного случайного процес-

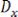
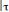
са может быть аппроксимирована выражением , где

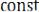– параметр затухания.

5. Если случайная функция имеет периодическую составляющую, то корреляционная функция также содержит периодическую составляющую той же частоты.

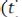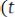
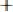
6. Чем слабее взаимосвязь между предыдущими и последующими 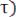значениями случайного процесса, тем быстрее убывает корреляционная функция.

Числовой характеристикой, служащей для оценки скорости изменения реализаций случайного процесса, является интервал корреляции

1 ¥

tk = K (0) ò0 K (t) dt.

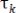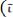
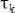
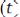
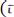
Вероятностный прогноз случайного процесса возможен на время (если известна информация о поведении какой-либо реализации в прошлом). Осуществлять прогноз на время, большее, чем нельзя, так как мгновенные значения, столь далеко отстоящие во времени практически некоррелированы, т. е. среднее значение произведения 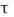стремится к нулю.

125