Обычно при создании стереограмм ставится задача показать пространственно разделённые по координатеz части изображения, то есть изображение всегда представляется как плоскость, деформированная по координатеz. При этом для описания каждой точки этой плоскости(на рисунке 56: точки A и B) используются как минимум два пикселя, дающих её изображение (AL и AR) соответственно для левого ( L1 ) и правого ( R1 ) глаза вдоль одной горизонтальной строки. Два изображения следующей «трёхмерной» точки (B) в наиболее простых алгоритмах пиксели строится для смещённых на малое расстояние h точек зрения левого ( L2 ) и правого ( L2 ) глаза. Чем ближе точка к плоскости изобра-

жения, тем меньше расстояние между изображающими её пикселями. В результате такого подхода: (1) глазные оси, рассматривающий изображение, должны быть практически параллельны, иными словами, «глаз должен быть аккомодирован на бесконечность»; (2) информация о цвете трёхмерного изображения для таким образом обманутого глаза обычно намеренно не поддерживается, чтобы зашифровать трёхмерное изображение за цветной двумерной основой; (3) для стереограммы задаётся период повторения, обычно равный нескольким сантиметрам, в который и вписывается трёхмерное изображение. Упорядоченного по данным правилам расположения пикселей для фиксированного фокусного расстояния D вполне достаточно, чтобы мозг человека, постоянно настроенный на поиск форм в информационном поле, соответствующим образом настроил восприятие «скрытой» информации и дал чёткое восприятие опрокинутого в глубину изображения.

6.5. Алгоритмические основы трёхмерной графики

6.5.1. Преобразования координат

Преобразования координат в явном и неявном виде широко используются в компьютерной графике с целью описания графического объекта в наиболее удобных координатных системах, для изменения масштаба элементов чертежа, построения проекций пространственных образов, направленной деформации объектов.

Пусть задана n–мерная система координат в базисе( k1 , k2 ,… kn ), описы-

вающая положение точки в пространстве с помощью числовых значений ki . Ес-

ли задать другую, N–мерную систему координат в базисе( m1 , m2 , … mN ) и по-

ставить задачу определения координат в новой системе, зная координаты в старой, то решение (если оно существует) можно записать в таком виде:

120

m1	= f1 (k1 , k2 ,...kn ),
m2	= f2 (k1 , k2 ,...kn ),
	(46)
	...
mN	= f N (k1 , k2 ,...kn )

где fi – функции пересчёта i-й координаты.

По виду функций преобразования различают линейные и нелинейные преобразования. Если при всех i = 1, 2, …, N функции fi – линейные относи-

тельно аргументов ( k1 , k2 ,...ki ), то есть:

fi = ail k1 + ai 2 k2 + ... + ain kn + ain+1

(47)

где ail – константы, то такие преобразования называют линейными, а при

n= N – аффинными14.

Вкомпьютерной графике наиболее распространены двумерные и трехмерные аффинные преобразования. В таких преобразованиях особую роль играют несколько важных частных случаев: поворот (вокруг начальной точки), растяжение (сжатие), отражение и сдвиг (перенос). Любое аффинное преобразование может быть представлено в виде последовательности таких простейших геометрических операций.

Классические геометрические преобразования (сдвиги, повороты) описываются с помощью математических моделей, основанных на использовании матриц размера 3х3. При классическом подходе каждое из преобразований представляется отдельной матрицей. Для компьютерной графики это часто приводит к неоправданному увеличению объема вычислений, и, следовательно, к снижению скорости вывода графической информации. Поэтому используется математический аппарат, обеспечивающий более компактное описание геометрических преобразований.

Рассмотрим метод однородных координат.

14

Аффинное преобразование (affine maping) – точечное взаимно-однозначное отображение плоскости на себя, при котором трем точкам, лежащим на одной прямой, соответствуют три точки, также лежащие на одной прямой. Аффинное преобразование переводит пересекающиеся прямые в пересекающиеся, параллельные - в параллельные. Плоскости в трехмерном пространстве при этом также остаются плоскостями, параллельные плоскости – параллельными. За исключением вырожденных случаев все точки первичной плоскости(или пространства) преобразуются и заполняют все точки вторичной плоскости.

121

éa11 a 12

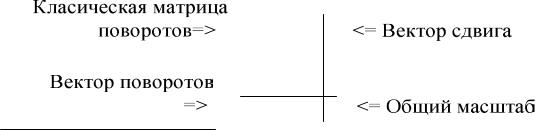
Воснове этого метода лежит представление о том, что каждая точка в N– мерном пространстве может рассматриваться как проекция точки из(N+1) – мерного пространства.

Вчастности, точка в трехмерном пространстве представляется четырьмя составляющими, например, ее координаты будут заданы как V=(x, y, z, w).

Если w не равно 1, то декартовы координаты точки (X,Y,Z) получаются из соотношения15:

[ X Y Z 1] = [(x / w) ( y / w) (z / w)1] .

(48)

Свойства однородных координат позволяют выражать с помощью единой матрицы все преобразования: сдвиги, повороты и даже проекции, а также любые сочетания преобразований в виде произведения матриц. Использование однородных координат позволяет применять единых математический аппарат для пространственных преобразований (поворотов, масштабирования, переноса) точек, прямых, квадратичных и бикубических поверхностей и линий.

Матрица однородных координат представлена в виде формулы (49):

ìX = a11 x + a12 y + a13 z + d

ï

íY = a21 x + a22 y + a23 z + e . ïîZ = a31 x + a32 y + a33 z + f

В матричном виде:

éX ù		éxù
ê	ú	ê	ú
êY	ú	= M êyú		,
êZ ú		êz ú
ê	ú	ê	ú
ë 1	û	ë1	û

(49)

(50)

где матрица преобразований M имеет следующий вид:

a13 dù

êêa 21 a 22 a 23 eúú

êêa 31 a 32 a 33 f úú

ëm n k Sû

15

Если мы хотим работать только с целыми числами, w выступает в качестве масштабного коэффициента.

122

Обычно на практике используютсянормализованные координаты (параметр S равен 1). Создавая различные программы трехмерного моделирования, требуется прежде всего реализовать подмножество векторных и матричных операций. Используя аппарат однородных координат, разрабатывать системы визуализации трехмерных изображений становится намного проще и удобнее.

Примеры основных элементарных преобразований, выражаемых с помощью матрицы однородных координат (51):

Поворот на угол j	Поворот на угол y вокруг оси
вокруг оси x	y

	é1		0	0	0ù
M	ê			sin(j) 0		ú	My
	= ê0 cos(j)					ú
x	ê	0	-sin(j) cos(j) 0			ú
	ê					ú
			0	0
	ë0				1û

	Поворот на угол
			оси z
	é cos(q) sin(q)
M	ê
	= ê-sin(q) cos(q)
z	ê	0	0
	ê	0	0
	ë

é cos(y) 0			sin(y)	0 ù
ê				ú
= ê	0	1	0	0ú
ê-sin(y) 0			cos(y) 0 ú
ê	0	0	0	ú	(51)
ë				1û
вокруг		q

0 0 ù

0 0 úú

1 0ú

ú

0 1û

Результирующее преобразование представляет собой совокупность - по следовательных поворотов с заданными угламиφ, ψ, θ, вокруг координатных осей декартовой системы координат, связанной с рассматриваемым объектом сцены и записывается в итоге как произведение матрицM X ´ M Y ´ M Z . Таким образом, можно описать поворот системы координат объекта вокруг положения ее центра относительно фиксированной системы координат, связанной, например, с экраном, на произвольный угол.

Из аналитической геометрии известно, что последовательно выполняемые повороты некоммутативны, то есть результат зависит от порядка, в котором повороты совершались. В нашем случае, когда матрица M изначально транспонирована для последующего умножения на вертикальный вектор координат (так

123

как это принято вOpenGL), координаты точки после преобразования вычисляются так:

V * = M X × M Y × M Z ×V				(52)

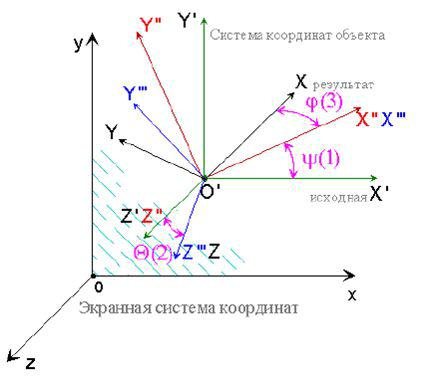
Вообще говоря, любое заданное направление осей объектной системы координат можно получить, выполняя три поворота вокругдвух координатных осей, при этом для первого (ψ) и третьего (φ) поворота берется одна ось, которая в процессе преобразования сама поворачивается(θ). Использовать такое преобразование предложил Леонард Эйлер, исследовавший вращения планет и волчков. На рисунке 56 представлена схема поворота системы координат из положения < x', y', z'> , совпадающего с положением экранной системы координат,

в некое произвольное положение<x, y, z>. При этом координаты видовой системы, связанной с объектом сцены, будут выражаться через координаты экранной системы с помощью легко получаемых выражений.

Рисунок 56 – Схема поворота системы координат из положения < x', y', z'>

в некое произвольное положение <x, y, z>.

Записанные ниже результирующие соотношения(53), определяющие положение точки с видовыми координатами (x, y, z) в координатах (X, Y, Z) экранной системы, приведены уже в виде произведения трехмерной матрицы преобразований на компоненты вектора (x, y, z):

124

X = (cosy × cosj - siny × cosq × sinj)x + (-cosy × sinj - siny × cosq × cosj) y + + (siny × sinq )z

Y = (siny ×cosj - cosy ×cosq ×sin j)x + (-siny ×sin j + cosy ×cosq ×cosj) y +
+ (-cosy ×sin q)z	(53)
Z = (sin q ×sin j) x + (sin q × cosj) y + (cosq)z .

Рассмотрим ещё несколько примеров матриц аффинных преобразований в однородных нормализованных координатах (матрицы невырожденные):

Сдвиг на вектор (смеще-

Растяжение (сжатие):

Отражение:

é1 0

0 aù

éa 0 0 0ù

é1 0 0 0ù

ние): M

ê

ú

ê

ú

ê

ú

s

= ê0

1

0

b ú

M

d

= ê0

b

0

0ú

M

rxy

= ê0

1

0 0ú

ê0

0

1

c ú

ê0

0

g

0 ú

ê0

0

-1 0ú

ê

ú

ê

ú

ê

ú

ë0 0 0 1û

ë0 0 0 1 û

ë0 0 0 1û

Здесь

осуществля-

Здесь

ненулевые

В

данном случае

ется перенос начала сис-

коэффициенты

растяже-

осуществляется операция

темы координат

объекта

ния α,β,γ

соответственно

отражения

относительно

на вектор с трехмерными

для осей x, y, z объектной

плоскости <xy>

координатами (a, b, c).

системы координат.

Таким образом, совокупность операции по преобразованию координат предмета описывается произведением матриц, которое затем приводится к еди-

16

ной матрице для всех элементов и точек объекта. Предположим, что задано осуществить повороты предмета на угол α вокруг оси, параллельной оси x, и на угол β вокруг оси z, проходящих через точку с координатами( x0 , y0 , z0 ). Эта операция будет описываться произведением четырех матриц: матрицы, описывающей сдвиг для совмещения точки ( x0 , y0 , z0 ) с началом координат; двух мат-

риц, описывающих повороты вокруг соответствующих осей; матрицы, описывающей сдвиг для возвращения точки в первоначальное положение.

16

Результирующее отображение объектов трёхмерной сцены определяется суперпозицией преобразований координат, принадлежащих отдельным объектам, группам объектов, и наконец всей сцене.

125