
- •Министерство образования и науки
- •Введение
- •Понятие о Золотом сечении
- •2.1. Золотое сечение – гармоническая пропорция
- •2.2. Второе золотое сечение
- •Золотой треугольник
- •История золотого сечения
- •Ряд Фибоначчи
- •Обобщенное золотое сечение
- •Принципы формообразования в природе
- •Золотое сечение и симметрия
- •2. Методы одномерной оптимизации
- •Метод золотого сечения.
- •3. Практическая реализация метода золотого сечения
- •3.1. Характеристика объекта автоматизации
- •Разработка программы
- •Описание метода золотого сечения
- •Результаты
- •3.3 Обоснование выбора языка программирования
- •Заключение
- •Список использованных источников:
- •Приложение № 2.
- •Листинг программы.
- •Результат работы программы.
Министерство образования и науки
РОССИЙСКОЙ ФЕДЕРАЦИИ
Государственное образовательное учреждение
высшего профессионального образования
ФИЗИКО-МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ
Кафедра программирования и вычислительной математики
Направление: информатика
Курс V
КУРСОВАЯ РАБОТА
метод Золотого сечения
Научный руководитель:
____________________________
Дата представления_________________
Дата защиты_______________________
Оценка____________________________
Уфа 2012
Содержание
|
|
стр. | ||||
|
Введение |
3 | ||||
|
1 |
Понятие о Золотом сечении |
6 | |||
|
|
1.1. |
Золотое сечение – гармоническая пропорция |
6 | ||
|
|
1.2. |
Второе золотое сечение |
8 | ||
|
|
1.3. |
Золотой треугольник |
9 | ||
|
|
1.4. |
История золотого сечения |
11 | ||
|
|
1.5. |
Ряд Фибоначчи |
17 | ||
|
|
1.6. |
Обобщенное золотое сечение |
18 | ||
|
|
1.7. |
Принципы формообразования в природе |
20 | ||
|
|
1.8. |
Золотое сечение и симметрия |
24 | ||
|
2. |
Методы одномерной оптимизации |
25 | |||
|
|
2.1 |
Метод золотого сечения |
26 | ||
|
3. |
Практическая реализация метода золотого сечения |
30 | |||
|
|
3.1. |
Характеристика объекта автоматизации |
30 | ||
|
|
3.2. |
Разработка программы |
32 | ||
|
|
3.3. |
Обоснование выбора языка программирования |
37 | ||
|
Заключение |
39 | ||||
|
Список использованных источников |
41 | ||||
|
Приложения |
42 | ||||
Введение
Несмотря на то, что безусловная оптимизация функции одной переменной наиболее простой тип оптимизационных задач, она занимает центральное место в теории оптимизации как с теоретической, так и с практической точек зрения. Это связано с тем, что задачи однопараметрической оптимизации достаточно часто встречаются в инженерной практике и, кроме того, находят свое применение при реализации более сложных итеративных процедур многопараметрической оптимизации.
На
первый взгляд кажется, что задача
минимизации функции одного переменного
является довольно элементарной. В самом
деле, если функция
 (целевая
функция), которую нужно минимизировать
на отрезке
(целевая
функция), которую нужно минимизировать
на отрезке![]() ,
дифференцируема, то достаточно найти
нули производной, присоединить к ним
концы отрезка, выделить из этих точек
локальные минимумы и, наконец, среди
последних найти ту точку, в которой
достигается абсолютный минимум.
,
дифференцируема, то достаточно найти
нули производной, присоединить к ним
концы отрезка, выделить из этих точек
локальные минимумы и, наконец, среди
последних найти ту точку, в которой
достигается абсолютный минимум.
Однако
для широкого класса функций эта задача
не так уж проста. Во-первых, задача
решения уравнения
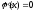 может оказаться весьма сложной. С другой
стороны, в практических задачах часто
не известно, является ли
может оказаться весьма сложной. С другой
стороны, в практических задачах часто
не известно, является ли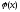 дифференцируемой функцией.
дифференцируемой функцией.
В силу этого существенное значение приобретают методы минимизации, не требующие вычисления производной.
Задачу
одномерной оптимизации можно поставить
следующим образом. Значения искомого
параметра x
должны быть заключены в интервале
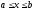 .
Назовем этот интервал интервалом
неопределенности. В начале процесса
оптимизации этот интервал имеет длину
.
Назовем этот интервал интервалом
неопределенности. В начале процесса
оптимизации этот интервал имеет длину .
Вычисляя последовательно значения
функции
.
Вычисляя последовательно значения
функции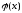 в крайних точках, интервал сужают. Таким
образом, большинство детерминированных
методов состоит в построении
последовательность отрезков
в крайних точках, интервал сужают. Таким
образом, большинство детерминированных
методов состоит в построении
последовательность отрезков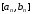 ,
стягивающихся к точке
,
стягивающихся к точке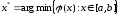 .
Однако всегда можно указать такую
непрерывную функцию
.
Однако всегда можно указать такую
непрерывную функцию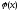 ,
что для любого конечного номера
,
что для любого конечного номера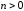 отрезок
отрезок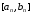 ,
построенный любым методом, не будет
содержать точку
,
построенный любым методом, не будет
содержать точку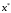 ,
даже если известен отрезок
,
даже если известен отрезок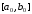 ,
которому принадлежит
,
которому принадлежит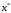 .
В связи с этим гарантировать принадлежность
точки
.
В связи с этим гарантировать принадлежность
точки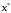 отрезку
отрезку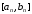 можно лишь для определенных классов
минимизируемых функций. Обычно
ограничиваются классов строго унимодальных
функций.
можно лишь для определенных классов
минимизируемых функций. Обычно
ограничиваются классов строго унимодальных
функций.
Непрерывную
функцию
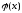 называютстрого
унимодальной,
если существует единственная точка ее
минимума
называютстрого
унимодальной,
если существует единственная точка ее
минимума
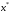 и
и
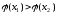 для
любых
для
любых
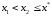 ,
,
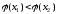 для любых
для любых
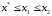 .
.
Таким
образом, с возрастанием x
функция
 слева от точки минимума монотонно
убывает, а справа от этой точки монотонно
возрастает.
слева от точки минимума монотонно
убывает, а справа от этой точки монотонно
возрастает.
Длина
интервала неопределенности
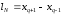 при известном
при известном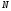 экспериментов, дающего номер
экспериментов, дающего номер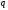 ,
и самих
,
и самих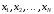 ,
выбранных их тех или иных соображений,
то есть
,
выбранных их тех или иных соображений,
то есть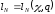 (
(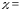
 ).
).
Чтобы
определить рациональную стратегию (или
ее начальную фазу) заранее, не приступая
к экспериментам, достаточно рассмотреть
следующие условия: если
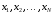 выбраны и тем самым задан ряд интервалов
выбраны и тем самым задан ряд интервалов ,
то какой-то из них имеет наибольшую (по
сравнению с остальными) длину
,
то какой-то из них имеет наибольшую (по
сравнению с остальными) длину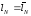 .
Приняв в качестве
.
Приняв в качестве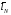 в качестве характеристики выбранной
совокупности
в качестве характеристики выбранной
совокупности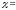
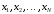 ,
можно быть уверенным в том, что реальный
результат поиска
,
можно быть уверенным в том, что реальный
результат поиска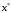 при этих
при этих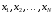 ,
оцениваемый величиной
,
оцениваемый величиной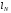 ,
будет лучше (или по крайней мере не хуже)
,
будет лучше (или по крайней мере не хуже)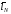 .
Очевидно,
.
Очевидно,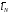 ,
заданная как
,
заданная как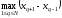 ,
является функцией только
,
является функцией только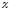 (принятая
ориентация на худший случай дает гарантию
от непредвиденных осложнений, которые
могут возникнуть в ходе проведения
экспериментов). Если теперь рассмотреть
множество стратегий с показателями
(принятая
ориентация на худший случай дает гарантию
от непредвиденных осложнений, которые
могут возникнуть в ходе проведения
экспериментов). Если теперь рассмотреть
множество стратегий с показателями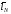 ,
то лучшей из них следует признать ту,
которой соответствует наименьшая
величина
,
то лучшей из них следует признать ту,
которой соответствует наименьшая
величина (преимущество такого выбора в том, что,
во-первых, сохраняется гарантия получить
реальную длину интервала неопределенности,
не превышающую
(преимущество такого выбора в том, что,
во-первых, сохраняется гарантия получить
реальную длину интервала неопределенности,
не превышающую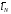 ,
и во-вторых, эта гарантированная длина
минимальна). Обозначив рассматриваемый
минимум
,
и во-вторых, эта гарантированная длина
минимальна). Обозначив рассматриваемый
минимум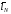 как
как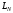 ,
получим
,
получим
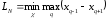
Величина
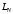 определяет единственную стратегию,
называемую минимаксной. Всякое отклонение
от нее приведет лишь к опасности ухудшения
результат будущего поиска. Большое
преимущество использования критерия
определяет единственную стратегию,
называемую минимаксной. Всякое отклонение
от нее приведет лишь к опасности ухудшения
результат будущего поиска. Большое
преимущество использования критерия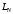 заключается в возможности априорного
выбора оптимального поиска экстремума.
заключается в возможности априорного
выбора оптимального поиска экстремума.
