ТЭЦ лекции

факт, что в узлах электрической цепи заряды не накапливаются и не расходуются. Часто первый закон Кирхгофа называют

уравнением баланса токов.

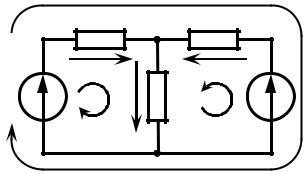
На основании первого закона Кирхгофа можно составить уравнение баланса токов и для, так называемого, обобщенного узла, который представляет собой часть схемы замещения цепи, охваченную произвольной замкнутой линией, называемой следом сечения. На рисунке 3.4 штриховой линией показан такой след сечения. Тогда для сформированного обобщенного узла можно записать уравнение баланса токов

i1(t)−i2 (t)−i3 (t)

i1

		c
	R1	i4
e	i5	R3
i3

=0. (3.3)

R2
i6	d
	i2

Рисунок 3.4

Нетрудно убедиться, что последнее равенство может быть получено из уравнений баланса токов для всех узлов схемы на рисунке 3.4:

i1 −i4 −i6 = 0 – для узла c, −i2 + i5 + i6 = 0 – для узла d, −i3 + i4 −i5 = 0 – для узла e.

Суммируя три последних равенства, придем к выражению (3.3) баланса токов для обобщенного узла.

60

Второй закон Кирхгофа

Взамкнутом контуре в любой произвольный момент времени алгебраическая сумма напряжений на элементах контура равна алгебраической сумме ЭДС, действующих в контуре.

Всоответствии со вторым законом Кирхгофа для каждого контура можно составить уравнение баланса напряжений:

∑±uk (t)=∑±ek (t).		(3.4)
k	k

Прежде чем составить уравнение баланса напряжений необходимо указать направление обхода соответствующего контура, а затем сопоставить заранее заданные положительные направления напряжений на элементах и ЭДС в контуре с направлением обхода. Если положительное направление напряжения или ЭДС совпадает с направлением обхода, то эта составляющая в выражении (3.4) берется со знаком "плюс", если не совпадает – со знаком "минус".

На рисунке 3.5 приведена трехконтурная схема электрической цепи. Контуры включают в себя следующие ветви: e1-

R1-R2 − первый контур; e2-R3-R2 − второй контур; e1-R1-R3-e2 − третий контур. Запишем уравнение баланса напряжений для

третьего контура. Выберем произвольно направление обхода контура: положим, что оно соответствует обходу по часовой стрелке. В этом случае второй закон Кирхгофа запишется в виде

R1

u1

u2

e1

R3

u3

R2

e2

Рисунок 3.5

61

u1(t)−u3 (t)=e1(t)−e2 (t). (3.5)

Второй закон Кирхгофа является следствием закона сохранения энергии и указывает на то, что энергия, потребляе-

мая цепью от независимых источников, равна энергии, затрачиваемой цепью на перенос заряда.

Законы Кирхгофа являются основополагающими при определении значений токов и напряжений в электрической цепи.

Общее число уравнений баланса токов и баланса напряжений, очевидно, равно сумме числа узлов и числа контуров исследуемой цепи. Из математики известно, что решение системы уравнений возможно только в случае, если используемые уравнения являются линейно независимыми, то есть ни одно из уравнений не является линейной комбинацией других уравнений. Однако можно убедиться, что не все уравнения баланса токов и напряжений являются линейно независимыми. Так, для цепи, схема которой изображена на рисунке 3.6, можно записать уравнения первого закона Кирхгофа

−i1(t)−i2 (t)+ j1(t)=0 – для узла c,
+i2 (t)−i3 (t)+ j2 (t)=0 – для узла d,	(3.6)

+i1(t)+i3 (t)− j1(t)− j2 (t)=0 – для узла e.

Всистеме (3.6) уравнение для e-го узла может быть по-

лучено, если почленно сложить первое и второе уравнения системы и результат суммирования умножить на "минус" еди-

	c	d
	R2	i2
j1	R1	R3	j2
	i1	i3

e

Рисунок 3.6

62

ницу. Аналогично можно показать, что уравнение для узла c есть сумма третьего и второго уравнений с последующим умножением правой и левой частей полученного равенства на "минус" единицу. Итак, в этой цепи только любые два уравнения из трех являются линейно независимыми.

Для схемы, показанной на рисунке 3.5, имеют место три уравнения баланса напряжений

u1(t)+u2 (t)=e1(t),
u2 (t)+u3 (t)=e2 (t),	(3.7)
u1(t)−u3 (t)=e1(t)−e2 (t).

Предлагается читателю самостоятельно определить линейно независимые уравнения, составленные по второму закону Кирхгофа.

Системой независимых узлов или системой независи-

мых контуров принято называть совокупность узлов и контуров цепи, для которых можно составить систему линейно независимых уравнений по законам Кирхгофа. Определение числа независимых узлов и контуров, а также выделение соответствующих систем уравнений является одной из основных задач топологического анализа цепей, решение которой облегчается при использовании теории графов.

3.4.Ф Графы схем электрических цепей

3.4.1 Понятия о направленных графах

Графом цепи называют геометрическое представление схемы цепи, в котором каждый идеализированный элемент изображается в виде отрезка произвольной формы. Такие отрезки называют ветвями графа, а точки их соединения − уз-

лами или вершинами.

Граф цепи строят по ее схеме замещения. При этом каждую ветвь цепи заменяют ветвью графа, а каждый узел цепи

63

преобразуют в узел графа. На ветвях графа стрелками указывают их направление, совпадающее с направлением токов в ветвях схемы; такой граф часто называют направленным. Нумерация ветвей и узлов графа та же, что и нумерация ветвей и узлов схемы цепи.

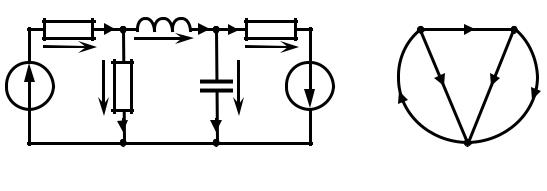
На рисунке 3.7, а приведена схема замещения некоей цепи, а на рисунке 3.7, б − направленный граф данной цепи.

Если узел графа является концом или началом какойлибо ветви, то считают, что узел и соответствующая ветвь инцидентны. Таким образом, каждая ветвь графа инцидентна двум узлам. Часть графа, которая содержит некий набор ветвей и инцидентных им узлов, называют подграфом.

Путь – это подграф, в составе которого ветви соединены так, что каждому узлу инцидентны две ветви, а граничным узлам – инцидентно по одной ветви. Таким образом, путь представляет собой набор ветвей графа, в котором все узлы соединены между собой, а все ветви подграфа представляют собой последовательное соединение, поэтому при обходе пути каждая ветвь и каждый узел встречаются только один раз.

Замкнутый путь, у которого начальный и конечный узлы совпадают, называется контуром. Очевидно, что между контурами графа и контурами цепи существует взаимная однозначность.

Связный граф – граф, в котором между любыми двумя узлами существует хотя бы один путь.

R1	c L		d	R3		c	d
u1	i1	u3 i3 i5		u5			2 3 4
e1	u2	R2 С		u4	e2	1	5
		i2	i4
		e					e
		а	Рисунок 3.7				б
				64

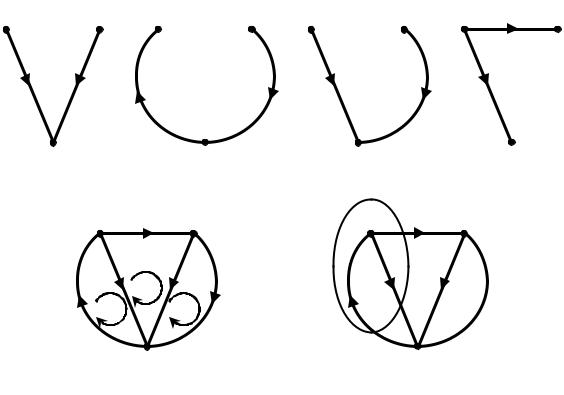
Дерево связного графа представляет собой подграф, включающий в себя все узлы графа, связанные между собой, но не образующие ни одного контура. Каждому графу может быть поставлено в соответствие несколько деревьев, отличающихся друг от друга составом ветвей дерева. На рисунке 3.8, а-г представлены несколько возможных (но не все) деревьев связного графа, соответствующего цепи, эквивалентная схема которой показана на рисунке 3.7, а (направленный граф такой цепи представлен на рисунке 3.7, б).

Следует заметить, что при построении дерева графа цепи не используются, так называемые, вырожденные ветви цепи,

включающие в себя идеальные источники тока.

Ветви, входящие в дерево графа, часто называют ребрами, а ветви, не вошедшие в дерево, называются хордами (связями, главными ветвями). Каждое из деревьев графа, содержащее q узлов, имеет m = q −1 ребер. Действительно, первая ветвь дерева принадлежит двум узлам, а каждая последующая

c		d c	d c
2	4		2

d	c	d
		2 3

1

5

5

e	e
а	б
c	d
	2 3 4

1 I II III5

ee

вг

c	d
	2 3 4

1 5

e	e
д	е

Рисунок 3.8

65

ветвь добавляет один узел. Если количество ветвей в графе равно p, число хорд n = p −q + 1.

Добавление к дереву графа одной хорды приводит к образованию контура, что можно видеть из графа на рисунке 3.8, д. Контуры, содержащие только одну хорду, называются главными контурами. Они образуются поочередным добавлением к дереву графа всех хорд. Таким образом, каждый главный контур содержит одну хорду, а остальные ветви – ребра.

Каждому дереву графа соответствует своя система из n = p −q + 1 главных контуров, причем главные контуры для каждого дерева отличаются друг от друга хотя бы одной ветвью, а именно ребром, входящим в главный контур.

Каждому главному контуру присваивают номер (на рисунке 3.8, д номера главных контуров указаны римскими цифрами). Направление обхода контура принимают, как правило, совпадающим с положительным направлением хорды.

Сечением графа называется минимальный набор ветвей графа, при удалении которого граф распадается на две изолированные части. Для нахождения набора ветвей, образующих сечение, граф рассекают на две части замкнутой линией, называемой линией сечения. На рисунке 3.8, е линия сечения обозначена штрихом. Если убрать набор ветвей 1-2-3, то образуются две изолированные части графа: изолированный узел c, ветви 4-5 с узлами d-e. Очевидно, что каждая из частей, на которые разделяется граф линией сечения, может рассматриваться как обобщенный узел. В таком случае для сечения можно записать уравнение баланса токов.

Главным сечением графа называется такое сечение, которое содержит только одно ребро, а остальные ветви – хорды. Тогда число главных сечений равно числу ребер m = q −1, где q – число узлов.

Каждому дереву может быть поставлена в соответствие своя система главных сечений, причем главные сечения,

66

соответствующие выбранному дереву, отличаются друг от друга хотя бы одной ветвью – ребром, входящим в дерево графа.

Главным сечениям графа присваивают номера и приписывают ориентацию, совпадающую с ориентацией ребра относительно линии сечения.

Если одна из частей, на которые делится граф, представляет собой изолированный узел, то такое сечение называется

каноническим.

3.5Определение числа независимых узлов

иконтуров

Уравнения относительно неизвестных токов и напряжений в цепи, составляемые по законам Кирхгофа, являются основой для расчета цепей. Однако эти уравнения должны быть линейно независимыми.

Из математики известно, что для констатации линейной независимости уравнений в системе используют необходимые и достаточные условия. Условие достаточности гласит, что система уравнений будет линейно независимой, если каждое из входящих в систему уравнений будет отличаться от остальных хотя бы одной переменной. Действительно, если любое из входящих в систему уравнений содержит хотя бы одну переменную, отсутствующую в других уравнениях, то данное уравнение не может быть получено в виде линейных комбинаций от других входящих в систему уравнений.

Таким образом, для линейной независимости уравнений, составленных по первому закону Кирхгофа, достаточно, чтобы каждое уравнение баланса токов отличалось от других уравнений хотя бы одним током или, что то же самое, чтобы каждый из узлов или каждое из сечений, для которых составляются уравнения баланса токов, отличались от других узлов или сечений хотя бы одной ветвью. Этому условию удовлетворя-

67

ют главные сечения графа, так как каждое из них отличается от остальных ребром дерева графа. Каждому дереву графа можно поставить в соответствие m = q −1 главных сечений; это позволяет составить m линейно независимых уравнений баланса токов. Можно показать, что число линейно независимых уравнений не изменится, если уравнения составлять не для главных сечений, а для узлов электрической цепи. Следовательно, любые (q −1) узлов электрической цепи образуют систему независимых узлов. При расчетах цепей обычно выбирают любые (q −1) узлов и записывают для них уравнения баланса токов, а для одного узла, который называют базисным, уравнения по первому закону Кирхгофа не составляются.

Для составления линейно независимых уравнений по второму закону Кирхгофа достаточно, чтобы каждое из этих уравнений отличалось от всех остальных уравнений хотя бы одним напряжением. То есть, чтобы выделенный набор контуров был независимым, достаточно, чтобы каждый контур отличался от остальных хотя бы одной ветвью. Такое условие выполняется для главных контуров выбранного дерева графа, так как каждый из главных контуров отличается от остальных хордой, входящей только в собственное уравнение главного контура. Так как число главных контуров для любого дерева графа равно n = p – q + 1, то в каждой цепи можно выделить n линейно независимых контуров и составить для них n линейно независимых уравнений по второму закону Кирхгофа.

Таким образом, общее число линейно независимых уравнений по первому и второму законам Кирхгофа оказывается равным числу ветвей рассматриваемой цепи:

m+n=(q−1)+( p−q+1)=p.

Для примера определим линейно независимые топологические уравнения для схемы, представленной на рисунке 3.7, а. Для этого:

1) составляют направленный граф (рисунок 3.7, б);

68

2)выбирают дерево графа; положим, что дереву графа соответствует рисунок 3.8, а;

3)приняв узел e за базисный, считают остальные узлы

c и d независимыми (рисунок 3.9, а);

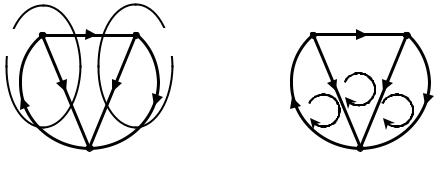
4) записывают уравнения баланса токов для главных сечений 1 и 2 (рисунок 3.9, а), которые совпадают с уравнениями баланса токов для узлов c и d:

i1(t) −i2(t) −i3(t) = 0, i3(t) −i4(t) −i5(t) = 0

(из системы уравнений баланса токов в цепи видно, что в первом уравнении фигурирует ток i1, отсутствующий во втором уравнении; в то же время во втором уравнении имеются токи i4 и i5, которых нет в первом; итак, два записанных уравнения являются линейно независимыми);

5) определяют линейно независимые контуры (добавив к дереву графа хорду 1, получают главный контур, образованный ветвями 1 и 2 (рисунок 3.9, б); при добавлении хорды 5 формируется главный контур из ветвей 4 и 5 и, наконец, добавление хорды 3 приводит к появлению третьего главного контура: ветви 2-3-4).

6) для независимых контуров схемы замещения записывают линейно независимые уравнения баланса напряжений:

u1(t) + u2(t) = e1(t) – для первого контура, u4(t) + u5(t) = −e2(t) – для второго контура, u3(t) + u4(t) – u2(t) = 0 – для третьего контура;

(далее следует проверить линейную независимость записан-

c	d	c		d
I	3 4	II	2	3 4
2
1	5	1	I	II	5
				III
	e а	Рисунок 3.9	б	e
		69