ТЭЦ лекции

Запишем независимые компонентные и топологические уравнения цепи, сформированные в предыдущем пункте:

u1(t)=i1(t) R1,
	i	(t)=C du2 (t)			,
	2			dt
	u	3	(t)=−i	(t) R	,
			3	2
i		(t)−i (t)+i (t)=0,
	1		2	3
u1(t)+u2 (t)=e1(t),
	−u2 (t)+u3 (t)=−e2 (t).

Примем за исходное базисное пятое уравнение (оно содержит информацию об одном из источников, порождающих процессы в цепи), в качестве независимой переменной, которая будет фигурировать в дифференциальном уравнении, – напряжение u2(t):

u1(t)+u2 (t)=e1(t).

Подставляя в последнее уравнение вместо исключаемой переменной u1(t) первое уравнение системы, получим

i1(t) R1 +u2 (t)=e1(t).

Исключим из полученного уравнения появившуюся в нем переменную i1(t). Для этого из четвертого уравнения системы выразим ток i1(t) = i2(t) – i3(t) и подставим его в полученное ранее уравнение:

[i2 (t)−i3 (t)] R1 +u2 (t)=e1(t).

Учитывая второе i2 (t)=C du2 (t)/dt и					третье i3 (t)=−u3 (t)/R2
уравнения системы, придем к выражению
C du2 (t)		+u3 (t) R +u			(t)=e (t).
	dt	R	1	2	1
		2
			80

Наконец, из шестого уравнения системы определим исключаемое напряжение u3(t) = u2 (t)−e2 (t) , подставив которое в равенство, получим

C du2 (t)		+u2 (t)−e2	(t) R +u		2	(t)=e (t).
	dt	R2		1		1

Раскрыв скобки и приведя подобные слагаемые, имеем

	du	2	(t)		R					R
C R				+ 1+	1	u		(t)=e	(t)+e (t)	1	.
	dt				R
1							2	1	2	R
					2					2

Напряжение u2(t) может быть определено из полученного неоднородного дифференциального уравнения первого порядка с постоянными коэффициентами. Цепь, описываемая дифференциальным уравнением n-го порядка, называется цепью n-го порядка.

Полученное дифференциальное уравнение цепи можно представить в более общем виде

a du2 (t) +a		2	u	2	= f (t),	(4.1)
1	dt
где a1 =R1 C, a2 =1+R1 /R2 ,	f (t)=e1(t)+e2 (t) R1 /R2.

Читателю предлагается самостоятельно получить дифференциальное уравнение той же цепи (схема представлена на рисунке 4.1, а), приняв, что положительные направления тока и напряжения на сопротивлении R3 совпадают между собой. Сопоставьте полученный результат с приведенным выше. Сделайте вывод.

4.5Решение уравнений электрического равновесия для цепей с сопротивлениями

Рассмотрим частный случай решения уравнений электрического равновесия электрических цепей, которые состоят

81

только из идеализированных элементов одного типа – сопротивлений.

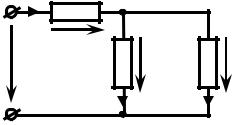
На рисунке 4.3, а представлена схема последовательного соединения сопротивлений нескольких (N) сопротивлений. Покажем, что последовательное соединение сопротивлений

i	R1	R2	. . .	RN	i	RЭ
	u1	u2		uN
		u				u
		а	Рисунок 4.3			б

может быть заменено одним эквивалентным сопротивлением, показанным на рисунке 4.3, б.

Составим уравнения электрического равновесия данной цепи. Компонентные уравнения элементов цепи запишутся в виде

u1 =i R1, u2 =i R2 , ... uN =i RN ,

а топологическое уравнение цепи:

u−u1 −u2 −...−uN =0

или	u =u1 +u2 +...+uN .

Подставляя компонентные уравнения в топологическое, приходим к уравнению

u =i (R1 +R2 +...+RN ).

Из последнего равенства видно, что последовательное

соединение сопротивлений можно заменить одним эквивалентным сопротивлением, величина которого определяется суммой сопротивлений:

RЭ =R1 +R2 +...+RN .	(4.2)
82

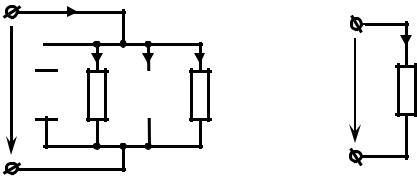
Эквивалентность цепей на рисунках 4.3, а и б подразумевает неизменность тока и общего напряжения на этих цепях. Иными словами, если к источнику электрической энергии подключить цепь на рисунке 4.3, а, а затем заменить ее на цепь, показанную на рисунке 4.3, б, сопротивление которой рассчитывается по формуле (4.2), то источник "не заметит" подмены – ток и напряжение на новой нагрузке никак не изменится.

Система уравнений электрического равновесия цепи с параллельным соединением N сопротивлений (рисунок 4.4, а) имеет вид

u

i i1 R1

i2	iN	i
..	u	RЭ
R2.	RN

а

Рисунок 4.4

б

i=i

+i

+...+i

N

,

1

u

2

u

u

i

=

, i

=

, ... i

=

,

R

R

R

1

2

N

N

1

2

откуда следует

1

1

1

u

i=u

+

+...+

=

.

R

R

R

N

R

1

2

Э

Из последнего выражения видно, что

1

=

1

+

1

+...+

1

.

(4.3)

R

R

R

R

Э

1

2

N

Заменив сопротивления в формуле (4.3) проводимостями, получим

83

GЭ =G1 +G2 +...+GN .

(4.4)

Таким образом, параллельное соединение сопротивлений R1…RN можно заменить одним эквивалентным сопротивлени-

ем RЭ =1/GЭ (рисунок 4.4, б). При параллельном соединении

сопротивлений складываются проводимости ветвей, определяя эквивалентную проводимость GЭ =1/RЭ .

Если параллельно соединены два сопротивления R1 и R2, то это соединение также можно заменить одним эквивалентным сопротивлением, величина которого рассчитывается по простой формуле, вытекающей из (4.3):

R =	R1 R2		.	(4.5)
Э	R +R
	1	2

И наконец, составим и проанализируем систему электрического равновесия цепи, в схеме которой сопротивления соединены смешанным образом (рисунок 4.5). Запишем систему электрического равновесия такой цепи:

i1	R1
u	u1	u2	R3	u3
	R2
		i2	i3
	Рисунок 4.5

i1 =u1/R1,i2 =u2 /R2 , i3 =u3 /R4 ,

i1 =i2 +i3,u=u1 +u2.

Из первого закона Кирхгофа и закона Ома для участков цепи получаем

84

i	=i	+i		u2		u2	=u			1		1		(4.6)
			=		+						+		.
				R		R				R		R
1	2	3						2
			2		3					2		3

Используя второй закон Кирхгофа из уравнений электрического равновесия цепи, из (4.6) получим

				1		1				1		1
	i =(u−u		)		+			=(u−i R )			+		.
				R		R				R		R
	1	1						1 1
				2		3				2		3

Выразив из выражения (4.7) напряжение u, получим

							1						R2 R3
	u =i	R		+					=i	R		+			.
					1/R		+1/R						R	+R
	1		1						1		1
					2		3						2	3

(4.7)

(4.8)

Из равенства (4.8) очевидно, что выражение, стоящее в скобках и связывающее между собой ток и напряжение на зажимах цепи, представляет собой эквивалентное сопротивление цепи

R =R +	R2 R3		.	(4.9)
Э 1	R +R
	2	3

Эквивалентное сопротивление цепи, показанной на рисунке 4.5 и представляющей собой тривиальный случай смешанного сопротивления, определяется как сумма двух сопротивлений R1 и R23 , одно из которых ( R23 =R2 R3 /(R2 +R3 ) ) рассчитывается как эквивалентное сопротивление параллельного соединения сопротивлений R2 и R3 .

Из рассуждений, приведенных выше, следует, что в цепях, содержащих только сопротивления, решение уравнений электрического состояния цепи существенно проще. Это обусловлено тем, что компонентные уравнения сопротивлений представляют собой алгебраические уравнения, что, в свою очередь, приводит к формированию алгебраического, а не ин- тегро-дифференциального уравнения цепи.

Уравнение (4.9) показывает, что схему цепи, представленную на рисунке 4.5, можно свести к схеме на рисунке 4.6, в

85

i1	R1
u	u1	u2
	R2

Рисунок 4.6

которой сопротивление R2 представляет собой эквивалентное сопротивление параллельного соединения R2 и R3 из схе-

мы рисунка 4.5. Схема цепи, состоящая из двух последовательно соединенных сопротивлений, называется схемой делите-

ля напряжения.

Из схемы делителя, показанной на рисунке 4.6, можно получить

u1 =i1 R1, u2 =i1 R2 ,

u =i1 (R1 +R2 ).

Рассматривая разные соотношения напряжений, фигурирующих в системе уравнений электрического равновесия цепи, приходим к следующим выражениям:

u1

=

R1

,

u1

=

R1

,

u2

=

R2

.

(4.10)

u

2

R

u

R +R

u

R +R

2

1 2

1

э

Из соотношений (4.10) можно сделать вывод, что в делителе

напряжений напряжения относятся между собой как сопротивления, к которым эти напряжения приложены.

4.6 Общие свойства решений уравнений цепи

Взадачах анализа электрических цепей широко используются свойства линейности дифференциальных уравнений. Рассмотрим эти свойства применительно к задаче анализа цепи, приведенной на рисунке 4.1, а. Такая цепь описывается уравнением вида (4.1).

Первое свойство: если изменить в k раз напряжения и токи всех действующих независимых источников цепи, то отклики цепи также изменятся в k раз.

Всилу линейности уравнения (4.1) умножение правой и левой частей уравнения на множитель k приводит к диффе-

86

ренциальному уравнению

a	d[k u2 (t)]		+a	2	[k u	2	(t)]=[k f (t)],	(4.11)
1	dt

Видно, что изменение в k раз правой части уравнения, обусловленной действием источников, приводит к умножению на тот же коэффициент напряжения (u2) в цепи.

Свойство линейности позволяет при расчетах линейных цепей вводить любой удобный масштаб для напряжений или токов, а также для элементов цепей. На основании этого свойства при решении задач удобно задавать значения элементов порядка единиц, т.е. уходить от чрезмерно малых или больших единиц измерения, а в полученном решении достаточно учесть их соотношение с условием задачи.

Второе свойство: если в дифференциальном уравнении цепи правая часть уравнения представляет собой производную или интеграл от воздействия, то отклик будет равен производной или интегралу от исходного отклика.

Это свойство вытекает из аналогии между исходным уравнением (4.1) и уравнением, получающимся после его дифференцирования

a	d 2u2 (t)	+a	2	du2 (t)	=df (t).	(4.12)
1	dt2			dt	dt

Согласно второму свойству, отклик цепи, например, на воздействие линейно нарастающего напряжения можно получить интегрированием отклика на более простое воздействие – постоянное напряжение.

Третье наиважнейшее свойство: в линейных электриче-

ских цепях результирующий отклик на воздействие, представляющее собой сумму составляющих, равен сумме откликов на каждую составляющую воздействия в отдельности.

Это свойство можно доказать следующим образом. Пусть правая часть линейного дифференциального уравнения

87

(4.1) определяется суммой двух составляющих f (t)= fa (t)+ fb (t).

Положим, что на цепь воздействуют поочередно fa (t) и fb (t) , что приводит к уравнениям

a	du2a (t)			+a	2	u	2a	(t)= f	a	(t),	(4.13)
1		dt
где u2a(t) – решение уравнения (4.13),
a		du2b (t)		+a	2	u	2b	(t)= f	b	(t),	(4.14)
1		dt

где u2b(t) – решение уравнения (4.14).

Суммирование уравнений (4.13) и (4.14) подтверждает сказанное

a1 d[u2a (t)+u2b (t)]+a2 [u2a (t)+u2b (t)]= fa (t)+ fb (t). (4.15) dt

Такое свойство линейных цепей является следствием из-

вестного из физики принципа наложения (суперпозиции).

Принцип наложения имеет исключительно большое значение в теории цепей. Для анализа линейной электрической цепи приложенный сигнал произвольной формы представляют, используя математический аппарат разложения функций, в виде суммы элементарных составляющих, которые позволяют проводить анализ цепи более простым методом. Искомый отклик цепи определяют суммированием элементарных откликов на действие каждой составляющей.

88

4.7 Тестовые задания для самопроверки

Задание 4.1. Введите правильный ответ.

Число линейно независимых уравнений, которые можно составить по первому закону Кирхгофа применительно к схеме на рисунке 4.7, равно …

Задание 4.2. Введите правильный ответ.

Число линейно независимых уравнений, которые можно составить по второму закону Кирхгофа применительно к схеме на рисунке 4.8, равно …

Задание 4.3. Введите правильный ответ.

Число линейно независимых уравнений, которые можно составить по второму закону Кирхгофа применительно к схеме на рисунке 4.7, равно …

R1
R2	R4
	R6

e

R3 R5

Рисунок 4.8

R1
R2	R4

e	j
R3	R5

Рисунок 4.7

Задание 4.4. Введите правильный ответ.

Число линейно независимых уравнений, которые можно составить по первому закону Кирхгофа применительно к изображенной на рисунке 4.9 схеме, равно …

Задание 4.5. Введите правильный ответ.

Число линейно независимых уравнений, которые можно составить по второму закону Кирхгофа применительно к схеме, изображенной на рисунке 4.9, равно …

Задание 4.6. Установите соответствие.

89