Башуров Методика решения математических задач 2011

Пример 8.5. Найти все дифференциальные операторы на полях.

Скалярное поле задано функцией f (x, y, z) = x2exyz2 ; векторное по-

ле задано векторной функцией a = x, y,i + y, z, j + zxk .

Начинаем решение с этапа 3. Поскольку на скалярном поле определен только градиент, то находим

f = (2xexyz2 + x2 yz2 )i + x3 z2ezyz 2 j + 2x3 yzk .

На векторном поле определены два оператора – ротор и дивер-

генция. Поскольку дальнейшее – это всего лишь дифференцирование по формулам (8.12) и (8.13), проводим все нужные операции: div a = y + z + x ,

i		j		k
∂ ∂ ∂					= i (−y) − j(z) + k (−x) .
∂x		∂y		∂z
xy		yz		zx

Этап 5 – проверка решения, на наш взгляд, состоит из повторения операций дифференцирования на случай ошибки в первоначальных вычислениях.

8.3. Задачи для самостоятельного решения

Найти трехгранник Френе для кривой:

	x = t,
8.1.				в точке t = –1.
	y = t2 ,
		3
	z = t
	x = t,
8.2.				в точке t = 1.
	y =1−t2 ,
	z = ln t
	x = a cos ϕ2 ,
8.3.				в точке ϕ= π.
	y = asin ϕ2 ,
			2
	z = bϕ

101

	x = t3 +1,
8.4.			3 +1,	в точке t = 0.
	y = −t
		2t
	z = e

x =

8.5. y =z =

x =

8.6. y =z =

r cos2 ϕcos θ,

−r sin ϕsin θ, если ϕ= θ = const . r cos θ− r,

et ,

sin t, в точке t = π2 . cost

8.7.	y = x2ex ,	в точке x = 1.
	z = x
8.8.	y = xex ,	в точке x = 2.
	z = x

Найти первую квадратичную форму Гаусса для поверхности:

	x = auv
8.9.
	y = b(u +v) .
		u
	z = c v
8,10.	z = sin(xy) .
8,11.	x2 − y2 = 2z .

x = a(u −v) 8.12. y = bu .

z = cuv

8.13. x2 − y = 2z2 . 8,14. x2 + 4 y2 + z =1 . 8.15. x2 +3y + z =1

Найти элемент площади dS и нормаль к поверхности:
			y2			1		1					1		1			11
8.16. x2		+				+ z2 =1 в точках A	,1,			,	B	−		,		,			.
			4			2		2					2		2			4
8.17.	x2	+		y2		+ z2 =1 в точке A(3,0,0).
9			16

102

Найти площадь поверхности:

8.18.x2 + y2 + z2 = 4 , x ≥ 0, y ≥ 0, z ≥ 0.

8.19.x2 + y2 + z2 = 9 , x ≥ 0, y ≥ 0, z≥ 0.

Вычислить поверхностные интегралы:
8.20. ∫∫	1+ 4x2 + 4 y2 dS ,			где S – часть параболоида вращения
S
z = 1–x2–y2, отсеченного плоскостью z = 0.
8.21. ∫∫x( y + z)dS , где S – часть цилиндрической поверхности
S
x = 1 − y2 , отсеченная плоскостями z = 0, z = 1.
8.22. ∫∫(3x2 +5y2 +3z2 − 2)dS ,						где S		–	часть	поверхности
S
y = x2 + z2 , отсеченная плоскостями y = 0, y = 1.
8.23. ∫∫	(x2 + y2 + z −	1	)dS ,		где		S	–	часть	поверхности
S	2
2z = 2 − x2 − y2 , отсеченная плоскостью Oxy.
8.24. ∫∫(x2 + y2 + z)dS ,				где	S	–	верхняя половина сферы
S
x2 + y2 + z2 = R2 .
8.25. ∫∫( y2 + z2 )dxdy , где S					–	верхняя			сторона	поверхности
S

z = 1 − x2 , отсеченная плоскостями y = 0, y = 1.

8.26. ∫∫(x2 + y + z2 )dxdz , где S – внутренняя сторона поверхно-

S

сти x2 = 2 y , отсеченная плоскостями y = 2, z = 0, z = 1.

8.27. ∫∫(x2 + y2 + z2 )dxdz , где S – внешняя сторона поверхности

S

y = x2 + z2 , отсеченная плоскостями y = 0, y = 1.

103

8.28. ∫∫(x2 + y2 + z2 )dydz , где S – внутренняя сторона части

S

полусферы x = R2 − y2 − z2 , вырезанная конусом x = y2 + z2 .

8.29. ∫∫ydydz + zdzdx + xdxdy , где S – внешняя сторона сферы

S

x2 + y2 + z2 =1.

8.30. ∫∫xdydz + ydzdx + zdxdy , где S – внешняя сторона сферы

S

x2 + y2 + z2 = R2 .

Вычислить:

8.31. grad f (x, y) , где f (x, y) = ln(ex2 +exy 2 ) + y .

			где f (x, y) = 1		y 2
8.32.	grad f (x, y)	в точках (1,3), (3,1),		−		.
				x

8.33.grad f (x, y) , где f (x, y) = x4 +sin( xy ) − xy в точке (1,1).

8.34.направление наибольшего и наименьшего роста функции

z = sin(x2 + y3 ) в точке ( π, 3 π) .

8.35. направление наибольшего и наименьшего роста функции

z = x2 y −exy + sin x в точке (1,1) .
		1+ y
8.36. div(rot a −grad f ), если a = yi + xj + xyzk , f = x2 + y2 + z2 .
8.37. div rot grad f			, где f	= x2 y3 .
8.38. div rot rot a ,			a = xi + y2 j + z3k .
8.39. rot a, grad f , div b ,				если	a = yzi + xzj + xyk ,
b = esin(xy)i +ln(xy) j ,			f = x2 sin(xyz) .
	dr				x = t,
8.40.		, если r (t) = rot a(t) и a(t) = xyi + yzj + zk , y =1,
	dt					2	.
					z = t

104

8.41. div rot a								и				grad div a ,													если					a = x2i +( y − z2 ) j + xyk ;
a = xi +( y + z2 ) j + x2 yzk .
8.42. div rot a ,																если													a = x2 y2i + x2z2 j + y2z2k ;
a = xyzi + xyj + xk .
Найти угол между градиентами скалярных																																				полей u(x,y,z) и
v(x,y,z) в точке М:
		yz2							x3										3							3								1				1
8.43.	u =					, v =								+ 6 y						+3 6z								, M				2,				,			.
		x		2						2																								2				3
8.44.	u =			z			,	v =		3				+	4				−	1				, M								1
																													1,2,					.
		x	3		y	2					x					y					6z											6
8.45. u = x2 yz3 , v =												4			6					6					3							1		3
																	−					+					,		M	2,			,			.
														x						9y					z							3		2
8.46. Найти производную функции																													z = 2x2 −5xy + 2y2 в точке

М (2,3) в направлении, составляющем с осью абсцисс угол α = 60° .

8.47. Найти	производную	функции		z = e−x 2 sin xy						в точке
М (2,–3) в направлении, составляющем				с осью					абсцисс угол
α = 30° .
8.48. Найти	производную	функции	z = x3 −3x2 y + 6xy2 +1 в
точке М (2,1) в направлении, идущем от этой точки к точке N (5,3).
8.49. Найти производную функции			z = xy+1			в точке М (1,1) в
						3		1
направлении, идущем от этой точки к точке N							,		.
						2
								2
8.50. Найти производную функции z = x y в точке М (2,2) в на-
правлении вектора l (2, 1) .
8.51. Найти	производную	функции	z = x3 y − zy + zx							в точке

М (2,1,3) в направлении, идущем от этой точки к точке N (3,3,7).

105

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1.Бекельман И.Я. Введение в дифференциальную геометрию. М.:

Наука, 1976.

2.Погорелов А.В. Дифференциальная геометрия. М.: Наука, 1974.

3.Фихтенгольц Г.М. Основы математического анализа. Т. 2. СПб.:

Лань, 2006.

4.Корн Г., Корн Т. Справочник по математике. Для научных работников и инженеров. М.: Наука, 1974.

106

Глава 9. РЯДЫ

9.4. Определения, основные теоремы и формулы

	∞	{an} – действительные
Определение 9.1.	Символ ∑an , где
	n=1

числа, называемый числовым рядом, обозначает предел (если он

существует) последовательности частичных сумм		k
	Sk = ∑an .
		n=1

В случае существования предела говорят, что ряд сходится, а сам предел называется суммой числового ряда (в дальнейшем – просто ряда).

Часто все слагаемые ряда задаются формулой an = f(n), позволяющей находить члены ряда при любом номере n.

Вопрос о значении суммы ряда принадлежит к проблеме бесконечности. На практике требуется сначала установить существование предела (т.е. суммы ряда), а затем в случае его существования превратить ряд в конечную сумму (т.е. заменить ряд его частичной суммой), а уж с ней мы можем поступать так, как нас учат в начальной школе. Вопрос о точности полученного значения суммы мы оставляем вне данного пособия.

Перечислим признаки существования суммы ряда, т.е. его сходимости.

Необходимым условием сходимости ряда является условие an → 0 при n → ∞ . Если ряд состоит только из неотрицатель-

ных чисел (положительный ряд), то присутствуют следующие

признаки.

∞

Теорема 9.1 (признак Даламбера). Пусть дан ряд ∑an и суще-

n=1

ствует предел lim an+1 =ρ. Тогда: 1) при ρ < 1 ряд сходится; 2) при

n→∞ an

ρ > 1 ряд расходится.

107

∞

Теорема 9.2 (признак Коши). Пусть дан ряд ∑an и существует

n=1

предел lim n an =ρ. Тогда: 1) при ρ < 1 ряд сходится; 2) при ρ > 1

n→∞

ряд расходится.

Теорема 9.3 (интегральный признак). Пусть дан ряд

∞

f(1)+ f(2)+ f(3)+…+ f(n)+…= ∑ f (n) ,

n=1

члены которого являются значениями некоторой функции f(x), положительной, непрерывной и убывающей на полуинтервале [1,∞). Тогда:

+∞	∞
1) если ∫	f (x)dx сходится, то сходится и ряд ∑ f (n) ;
1	n=1

+∞

2) если же ∫ f (x)dx

1

дится.

∞

расходится, то ряд ∑ f (n) также расхо- n=1

∞

Теорема 9.4 (теорема сравнения). Пусть даны два ряда ∑bn и

n=1

для всех n выполняется неравенство an ≤ bn . Тогда из сходимости

∞	∞
ряда ∑bn	следует сходимость ряда ∑an , а из расходимости ряда
n=1	n=1
∞	∞

∑an следует расходимость ряда ∑bn .

n=1

n=1

Замечание. Если ряд содержит конечное число отрицательных членов, то все перечисленные выше теоремы могут быть применены и к нему.

Если ряд состоит из строго чередующихся по знаку членов, то такой ряд называется знакочередующимся, и для установления существования суммы возможно применение признака Лейбница.

Теорема 9.5 (признак Лейбница). Если абсолютные величины

∞

членов знакочередующегося ряда ∑(−1)n+1 an монотонно убывают:

n=1

и общий член ряда стремится к нулю: liman = 0 , то ряд сходится.

n→∞

108

В случае произвольного знакопеременного ряда (т.е. мы не можем отнести ряд ни к положительным, ни к знакочередующимся, так как расположение положительных и отрицательных членов в

ряде произвольно) можно использовать следующую теорему. Теорема 9.6. Рассмотрим какой-нибудь знакопеременный ряд

∞
a1+ a2+ a3+…+ an+…= ∑an .	(9.1)
n=1
Одновременно рассмотрим ряд, составленный из абсолютных
величин членов ряда (9.1):
∞
|a1|+ |a2|+ |a3|+…+ |an|+…= ∑| an | .	(9.2)
n=1

Если ряд (9.2) сходится, то сходится и ряд (9.1) . В этом случае говорят, что ряд (9.1) сходится абсолютно.

Последняя теорема переводит решение вопроса о существовании суммы вашего ряда (произвольного) в область положительных рядов, а для них мы уже привели перечень пригодных для решения теорем.

Нетрудно увидеть, что применение всех вышеуказанных теорем не гарантирует решения вопроса о существовании суммы ряда. Поэтому, перебрав (но на законном основании!) все теоремы и не получив ответа, не расстраивайтесь – ваше «справочное бюро» не содержит необходимых для решения задачи теорем и формул. Возможно, их вообще не существует.

Для установления факта существования суммы ряда предлагаем использовать схему поиска решения, представленную на рис. 9.1.

Ряды, у которых слагаемые являются не действительными числами, а функциями переменной x, называются функциональными.

Сходимость такого ряда зависит от значения аргумента x, при этом при каждом фиксированном значении x функциональный ряд превращается в числовой. Установление области сходимости такого функционального ряда в общем случае приводит к необходимости перебора всех значений аргумента, что является невыполнимой задачей. Однако для специальных рядов можно избежать этой невыполнимой процедуры. К таким рядам относятся степенные ряды и ряды Фурье. Обратимся сначала к степенным рядам.

109

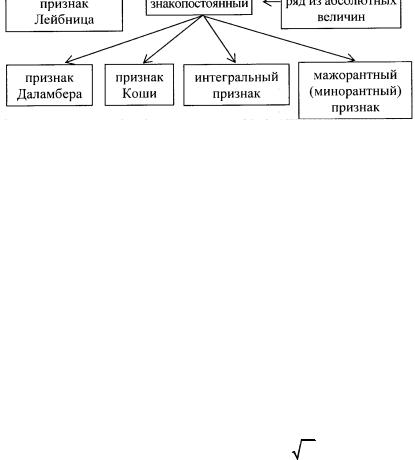
Рис. 9.1

Степенным рядом называется функциональный ряд, у которого общий член задается простой формулой an = bn xn , где n – нату-

ральные числа, а {bn}, называемые коэффициентами степенного ряда, – какие-то действительные числа.

∞

Область сходимости степенного ряда ∑bn xn не «больше» сег-

					n=1
мента [–R,R] и не «меньше» интервала (–R,R), где R – радиус схо-
димости степенного ряда, который определяется формулами:
R =	1	,	ρ = lim	bn+1	или ρ = lim n bn .	(9.3)
	ρ		n→∞ bn		n→∞

Чтобы окончательно решить вопрос об области сходимости, требуется проверить на сходимость только два (!) числовых ряда:

∞∞

∑bn Rn и ∑bn (−R)n .

n=1 n=1

Как видите, нам удалось в случае степенных рядов решить проблему перебора бесконечного числа точек.

Рассмотрим ряды Фурье на произвольном промежутке длиной 2l. Он имеет вид разложения вектора в бесконечномерном пространстве, в котором в качестве базиса выступает множество три-

110