Башуров Методика решения математических задач 2011

2) ∫ f (М)ds = ∫ f (М)ds ;

M0 M1 M1M0

3) ∫ f (М )ds = ∑∫ f (M )ds , если кривая Г представима в виде

Г k Гk

объединения набора кривых {Гk }, имеющих общими только гра-

ничные точки.

Если кривая Г задана параметрически, т.е. x =ϕ(t), y = ψ(t),

z = χ(t), то для вычисления интеграла удобно воспользоваться

формулой ds = dx2 + dy2 + dz2 , и тогда криволинейный интеграл

перейдет в определенный интеграл:

t1

∫ f (ϕ(t ),ψ(t ),χ(t )) ϕ′2 (t )+ ψ′2 (t )+ χ′2 (t )dt .

t0

Здесь t0 и t1 – значения параметра t, отвечающие начальной и конечной точкам кривой.

Если кривая замкнутая (т.е. любая ее точка может считаться начальной и одновременно конечной), используют обозначение

	∫ f (М )ds .
	Г
Определение 7.2. Если в качестве сомножителей в интеграль-
N
ную сумму ∑ f (Mk )	sk вместо sk входят проекции криволи-
k =1
нейного отрезка sk	на координатные оси, то предел этих сумм

определяет набор криволинейных интегралов второго рода и, в случае плоской кривой, они обозначаются

∫P (x, y)dx и ∫Q(x, y)dy .

ГГ

Обычно эти два интеграла соединяют вместе и имеют дело с одним криволинейным интегралом

∫P (x, y)dx + Q (x, y)dy .

Г

81

Свойства этого интеграла те же, что и у интеграла первого рода (за исключением свойства 2). Вместо него имеет место соотношение:

∫ P (x, y)dx + Q(x, y)dy = − ∫ P (x, y)dx + Q (x, y)dy .

AB BA

Для вычисления криволинейного интеграла второго рода используют две возможности: 1) связывают интеграл второго рода с некоторым интегралом первого рода при помощи формул dx = cos αds и dy = sin αds , где α – угол между касательной к кри-

вой Г и осью x, т.е.	′
	tg α = yx . И тогда получают интеграл
∫ P (x, y)dx + Q(x, y)dy = ∫ (P (x, y)cos α + Q (x, y)sin α)ds .
AB	AB

Второй способ напрямую связывает вычисление интеграла второго рода с определенным интегралом. Если кривая, по которой производится интегрирование, задана уравнением y = ϕ(x), то

dy = ϕ′(x)dx

и

b

∫ P(x, y)dx +Q(x, y)dy = ∫(P(x,ϕ(x))+Q(x,φ(x))ϕ′(x))dx ,

AB

a

где a и b отвечают началу и концу кривой Г.

В случае какого-либо другого способа задания кривой Г ищите возможность выразить дифференциалы dx и dy через дифференци-

ал одной какой-нибудь переменной, не обязательно x или y. Теорема 7.1 (теорема Грина). Если Г – граница области D и

функции P(x,y), Q(x,y) непрерывны, вместе со своими частными производными первого порядка, в замкнутой области D+Г, то имеет место равенство:

∫P(x, y)dx +Q(x, y)dy = ∫∫ ∂Q			−	∂P dxdy ,
Г	D	∂x		∂y

где S – область внутри кривой Г.

Теорема 7.2. Если во всей области D выполнено соотношение

∂P ∂Q

∂y = ∂x , то:

82

а)	интеграл	∫ P(x, y)dx + Q(x, y)dy	по любой замкнутой кри-
		Г
вой Г, целиком лежащей в области D, равен нулю;
б)	интеграл	∫ P(x, y)dx +Q(x, y)dy	по любой кривой, соеди-
		AB

няющей точки А и B, равен одному и тому же числу;

в) интеграл ∫ P (x, y)dx + Q (x, y)dy может рассматриваться как

AB

функция конечной точки кривой AB , т.е. являться функцией двух переменных x и y, где x и y – координаты конечной точки кривой

AB .

Теоремы 7.1 и 7.2 очень важны при решении большинства задач на взятие криволинейных интегралов или задач, связанных с ними. Одной из таких задач является задача о нахождении потенциала по силовому полю.

		Определение			7.3.		Потенциалом			силового	поля
	F = P (x, y)i + Q (x, y) j					называется			функция	U(x,y), удовлетво-
ряющая тождествам:
					∂U	= P(x, y),		∂U	= Q(x, y).
					∂x			∂y
		Условием существования потенциала вновь является условие
	∂P	=	∂Q	, где в качестве функций P(x,y) и Q(x,y) выступают ком-
	∂y
			∂x

поненты «силового» вектора F .

Если установлено существование потенциала, то его выражение находится при помощи криволинейного интеграла второго рода

U (x, y)= ∫P(x, y)dx + Q(x, y)dy ,

(7.1)

AB

где А – произвольно выбранная точка, а кривая AB – любая кривая, соединяющая точки А и B(x,y).

83

7.2. Примеры решения задач

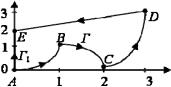
Пример 7.1. Найти криволинейный интеграл ∫(x2 + y2 ) dx + 2 yxdy по

Г

кривой Г, соединяющей точки A(0,0) и Е(0,2) и изображенной на рис. 7.1.

Рис. 7.1 Поскольку кривая не замкнута, да еще имеет «замысловатый вид», прямой способ взятия интеграла отпадает. Проверим выполнение ус-

ловия	∂P	=	∂Q	(здесь P = x2 + y2, Q = 2yx). Так как оно выполнено,
	∂y		∂x

мы можем вместо исходной кривой Г взять удобную для нас другую кривую Г1, изображенную на рис. 7.1, и после этого, учитывая, что на этой кривой dx = 0, получим представление криволинейного интеграла в виде одного простого интеграла.

На этапе 4 решения проводим все преобразования и вычисления (без лишних уже слов):

2

∫(x2 + y2 )dx + 2 yxdy = ∫2 yxdy = 0 ,

Г

0

так как на отрезке Г1 x = 0.

Несколько слов о приближенных методах вычисления определенных интегралов. Все они основаны на отказе от предельного перехода в суммах Римана и сводятся к конечному суммированию некоторых вполне определенных слагаемых. Точность приближенного интегрирования связана с одним или несколькими параметрами, называемыми шагом или шагами интегрирования, Процедура приближенного взятия интегралов позволяет вычислять интегралы с любой степенью точности. Это, в свою очередь, позволяет решение какой-либо задачи, представленное в виде интегралов, считать полученным. (Подробно об этом говорится в курсе «Вычислитель-

ная математика».)

Пример 7.2. Найти потенциал силового поля

F = y cos(xy) i + x cos(xy) j .

84

Сначала проверим, является ли силовое поле потенциальным.

Условие потенциальности – это выполнение равенства ∂Fx = ∂Fy .

∂y ∂x

Для нашего силового поля
	∂Fx	=		∂( y cos(xy))			=	xycos(− xysin)	xy) ,	(
	∂y				∂y
	∂Fy		=		∂(x cos(xy))		=	xycos(− xy sin)	xy)	(
	∂x				∂x

и условие потенциальности выполнено. Поскольку условие потенциальности одновременно является условием независимости криволинейного интеграла от пути интегрирования, то в формуле (7.1), дающей выражение для потенциала, мы можем выбрать путь ин-

тегрирования,	изображенный на
рис. 7.2.		y			B
Начальная точка пути интег-
		y			(x, y)
рирования может быть выбрана
произвольно и мы в этом каче-
стве выбрали начало координат.
Проведя	интегрирование в				A	x
формуле (7.1) и учитывая что		0		x
на отрезке АB dx = 0 и x = const,			Рис. 7.1

а на отрезке ОА dy = 0 и y = 0, получим ответ: U = sin(xy). Проверка заключается во взятии частных производных от по-

лученного выражения для потенциала и в сравнении их с компонентами исходного силового поля.

7.3. Задачи для самостоятельного решения

Вычислить криволинейные интегралы: 7.1. ∫xds , где Г – кривая y = x2, x [0,1].

Г
7.2. ∫2xyds , где Г – четверть эллипса	x2	+	y2	=1 , лежащая в
	4
Г		9

первом квадранте.

85

∫(x + z)ds , где Г

y =

3t2

3

7.3.

– дуга кривой x = t,

, z

= t , 0 ≤ t ≤ 1.

2

Г

7.4.

∫ x dx +

ydy , где Г – кривая y = x2, x [0,1].

Г

7.5.

∫ydx − xdy , где Г – дуга эллипса x = a cost, 0 ≤ t ≤ 2π.

Г

y = bsin t,

7.6.

∫x2 dx − y2 xdy ,

где Г

– кривая,

заданная

уравнением

Г

y = (1−ex )

1

, 0 ≤ x ≤ 2.

1−e2

∫y sin

2

1

sin 2x

7.7.

xdx

+

x −

dy , где Г – отрезок прямой, со-

2

4

Г

единяющий точки А(0,0), В(1,1).

7.8.

∫ yxdx −(x2 + y2 )dy , где контур Г представлен на рис. 7.3.

Г

1

2

Г

C

A

B

1

2

2

3

Рис. 7.3

Рис. 7.4

7.9.

∫sin(x + y)dx + cos(x + y)dy , где контур Г представлен на

Г

рис. 7.4.

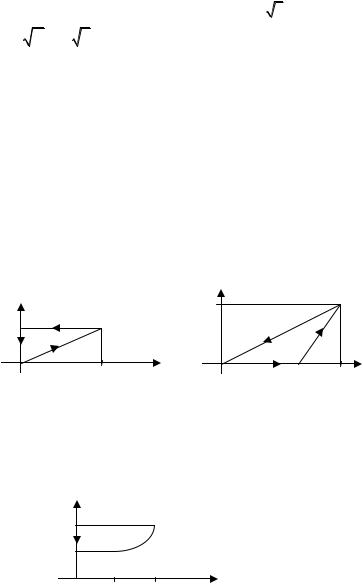
7.10. ∫ x2dx −xydy , где контур Г представлен на рис. 7.5.

Г

2 Г

y = (x – 1)2 + 1

1

1	2	Рис. 7.5

86

7.11.∫ x2 y3dy + 1x3 y2 dx , где контур Г представлен на рис. 7.6.

Г 3

	D 4						C
	–		A			B
Рис. 7.6			1	1		2	1

Найти потенциал силового поля:

7.12.F = xy2i + x3 y j .

7.13.F = 2x2 y3i + 2x3 y2 j .

7.14.F = x2 y i − ( y2 − yx) j .

7.15.F = xcos xy j + y cos xy i .

7.16.F = sin(x2 + y2 ) y i + cos(x2 + y2 )x j .

		3	2	2	x3		2
	7.17.	F =(x	+x y +xy		)i +		+αx y j , при каком α это воз-
						3

можно?

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1.Архипов Г.И., Садовничий В.А., Чубариков В.Н. Лекции по математическому анализу. М.: Высшая школа, 1999.

2.Фихтенгольц Г.М. Основы математического анализа. Т. 2. СПб.:

Лань, 2006. С. 137–178, 212–370.

3.Пискунов Н.С. Дифференциальное и интегральное исчисления.

Т. 2. М.: Физматлит, 1972. С. 160–253.

87

Глава 8. ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА

8.1. Определения, основные теоремы и формулы

Стандартное представление кривых, к которым сводятся любые формы их задания, имеет вид:

x = ϕ(t ),

r = r (t) или y = ψ(t ), (8.1)

z = χ(t ),

Стандартное представление поверхностей, к которым сводятся любые формы их задания, имеет вид:

x = ϕ(u,v),
	(8.2)
r = r (u,v) или y = ψ(u,v),

z = χ(u,v).

Векторные функции можно дифференцировать по тем же правилам, что и обыкновенные, так как они, по сути, есть не что иное, как две обыкновенные функции для векторов на плоскости и три – для векторов в пространстве.

Рассмотрим сначала кривые. Отметим на рассматриваемой кривой какую-либо произвольную точку М0 и введем естественную

параметризацию этой кривой, выбрав в качестве параметра длину дуги от точки М0 до произвольной точки М(x,y,z) этой кривой. По

формуле

t1
s = ∫ ϕ′2 (t )+ ψ′2 (t )+ χ′2 (t )dt	(8.3)
t0

найдем зависимость s от t. Обратив эту функцию, получим зависимость t = g(s) и, таким образом, получим уравнение кривой в натуральных координатах r = r (g(s)) или в координатной записи

x = ϕ(g (s)),

y = ψ(g (s)),

z = χ(g (s)).

88

Формулы Френе позволяют построить систему координат, привязанную к рассматриваемой кривой и меняющуюся от точки к точке этой кривой. В этом ее принципиальное отличие от неподвижной декартовой системы координат.

Рассмотрим некоторую точку М0 кривой:

dr

1) ds = τ0 , где τ0 – единичный вектор, направленный вдоль ка-

сательной к кривой в точке М0;

2)ddsτ0 = k n0 , где n0 – единичный вектор, перпендикулярный вектору τ0 , а k – кривизна кривой в точке М0;

3)dnds0 = −kτ0 + æ b0 где b0 – единичный вектор, называемый

«бинормалью», а коэффициент æ носит название «коэффициента кручения»;

4) последнее уравнение в системе уравнений Френе имеет вид:

ddsb0 = −æ n0 .

Построенная тройка единичных векторов τ0 , n0 и b0 образует базис, называемый трехгранником Френе.

Величина, обратная кривизне кривой, называется радиусом кривизны, и механическим аналогом этой величины является максимальный радиус колеса, которое может без толчков двигаться по

кривой в окрестности точки М0.
Стандартное представление поверхностей	имеет вид
r = r (u,v).
Частные производные от уравнения r = r (u,v)	по u и v в точке

поверхности М0(u0,v0) определяют два вектора Э1 и Э2 , которые вместе с точкой М0 задают касательную плоскость к поверхности в точке М0. Ее уравнение r − rM0 = uЭ1 + vЭ2 . Вектор [Э1, Э2 ] – век-

торное произведение векторов Э1 и Э2 , определяет направление нормали к поверхности в точке М0.

89

Если уравнение поверхности задано в виде z = f (x, y), то на-

правление нормали N в точке поверхности z = f (x, y) совпадает с градиентом функции ϕ(x, y, z)= z − f (x, y), т.е. можно положить

N = grad ϕ .

Первая квадратичная форма Гаусса для поверхности, заданной

x = ϕ(u,v),

уравнениями y = ψ(u,v), в точке поверхности определяется мат-

z = χ(u,v),

E	F	, где
рицей A =
F	G

E =

∂ϕ 2

∂ψ 2

∂χ 2

+

+

,

∂u

∂u

∂u

G =

∂ϕ 2

+

∂ψ 2

+

∂χ 2

,

(8.4)

∂v

∂v

∂v

F =

∂ϕ

∂ϕ

+

∂ψ

∂ψ

+

∂χ

∂χ

.

∂u ∂v

∂u ∂v

∂u ∂v

Квадратичная форма Гаусса имеет вид:

Edϕ2 + 2Fdϕdψ + Gdψ2.

(8.5)

Элемент длины элементарного отрезка, лежащего на поверхно-

x = ϕ(u,v),

сти, заданной системой уравнений y = ψ(u,v),

определяется че-

z = χ(u,v),

рез элементы первой квадратичной формы Гаусса выражением

ds =

Edu2 + 2Fdudv +Gdv2 .

Длина кривой, задаваемой

уравнениями u = ϕ(t ), v = ψ(t ), а

x = ϕ(u,v),

стало быть, лежащей на поверхности y = ψ(u,v), имеющей нача-

z = χ(u,v),

ло в точке М0(t0) и конец в точке М1(t1), вычисляется по формуле

90