Башуров Методика решения математических задач 2011

Глава 4. ИНТЕГРАЛЫ ОТ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

4.1. Определения, основные теоремы и формулы

Определение 4.1.Функция F(x) называется первообразной для функции f(x) на некотором промежутке X, если для всех значений x

dF

из этого промежутка выполняется равенство dx ≡ f (x) .

(Это выражение называется также простейшим обыкновенным

дифференциальным уравнением, но специально их мы рассмотрим в гл. 10.)

Множество всех первообразных функции F(x) называется неоп-

ределенным интегралом и обозначается ∫ f (x)dx .

Теорема 4.1. Если F(x) – первообразная для функции f(x) на некотором промежутке X, то любая другая первообразная для f(x) на том же промежутке может быть представлена в виде F(x) + С.

Часто употребляют термин «взять интеграл» вместо «найти первообразную».

Взятие интеграла, в отличие от взятия производной, представляет искусство, и поэтому взять интеграл не всегда удается так, чтобы в ответе получить элементарную функцию. В силу этого в процессе применения математики к прикладным задачам с использованием интеграла возникло много функций, которые называются «специальными» (в отличие от элементарных).

Поскольку редко удается (на практике) взять интеграл «точно», т.е. выразить ответ через элементарные функции, то следует сначала установить его существование. Эта проблема решается при по-

мощи определенного интеграла.

Определение 4.2. Пусть f(x) – некоторая функция, заданная на [a,b]. Разобьем промежуток [a,b] на маленькие сегменты [a = x0, x1], [x1, x2],…, [xn, xn+1 = b] длиной k, а максимальная длина которых не

превышает , и выберем на каждом таком сегменте произвольную точку ξk . Если сумма ∑ f (ξk ) xk имеет предел при числе раз-

k

биений, стремящихся к бесконечности, и при , стремящемуся к

51

нулю, и этот предел не зависит от выбора точек ξk ,то этот предел

называется «определенным интегралом от функции f(x) на проме-

b

жутке [a,b]» и обозначается ∫ f (x)dx .

a

Если рассматривать верхний предел как переменную величину, то оказывается, что определенный интеграл, рассматриваемый как функция верхнего предела, является первообразной для исходной функции f(x). Этот факт является содержанием великой теоремы Ньютона–Лейбница.

Формально для функции f(x) непрерывной на отрезке [a, b] теорема Ньютона–Лейбница имеет вид:

b

∫ f (x)dx = F (b)− F (a),

a

x

F (x)= ∫ f (ξ)dξ .

a

Теорема 4.2. Определенный интеграл существует для непрерывных функций, для функций, имеющих конечное число точек разрыва первого рода и для монотонных функций.

	Таким образом, эти две теоремы позволяют установить факт
						существования интеграла, будь он опре-
y
			f(x)			деленный или неопределенный.
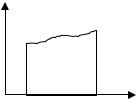
							Геометрический смысл определенного
						интеграла заключается в том, что если
						подынтегральная		функция неотрицатель-
							b
						x на,	то ∫ f (x)dx ,	если он существует, ра-
	a			b
							a
			Рис. 4.11			вен	площади криволинейной трапеции
						(рис. 4.1)

Приведем некоторые свойства определенного интеграла.

a

1. ∫ f (x)dx = 0 . a

ba

2.∫ f (x)dx = − ∫ f (x)dx .

ab

3.Свойство аддитивности:

52

			b		c	b
если [a,b] = [a,с] [с,b], то ∫ f (x)dx = ∫ f (x)dx + ∫ f (x)dx .
			a		a	c
4. Вынесение константы за знак интеграла:
b	b
∫c f (x)dx =	= c ∫ f (x)dx , если f(x) интегрируема на						[a, b],
a	a
с = const.
5. Свойство “плюс-минус”:
b		b	f (x)dx ±	b	g(x)dx ,
f (x)± g (x) dx =		∫		∫		если f(x) и g(x)	интег-
∫
a		a		a

рируемы на [a, b].

6. Замена переменных: если x =ϕ(t) дифференцируема на

[α, β], ϕ′(t ) непрерывна и не меняет знак на промежутке [α, β], где

b	β
ϕ(α) = a, ϕ(β) = b , то ∫ f (x)dx = ∫ f [ϕ(t)]ϕ′(t )dt .
a	α
	b			b
7. Взятие интеграла по частям: ∫u dv = uv			ba − ∫vdu , функции
	a			a

u(x), v(x) – непрерывны на [a, b] вместе со своими производными u′, v′.

Нахождение неопределенного и определенного интегралов, по сути, представляет одну и ту же задачу, за исключением одного момента: неопределенный интеграл существует, если подынтегральное выражение имеет смысл хотя бы на каком-нибудь промежутке, а определенный интеграл – только тогда, когда промежуток интегрирования полностью входит в область существования подынтегрального выражения.

К приведенным свойствам необходимо добавить и ряд интегралов, которые называются «табличными». Понятно, что количество «табличных» интегралов зависит от вашего опыта во взятии интегралов, а также от справочников, которые находятся у вас под рукой. Мы ограничимся следующими:

53

1.∫0 dx = C .

2.∫1 dx = x +C .

xn+1

3.∫xn dx = n +1 +C (n ≠ –1).

4.∫1x dx = ∫dxx = ln x +C .

	5. ∫ax dx =	ax	+C , ∫ex dx = ex +C .
		ln a

6.∫sin x dx = −cos x +C .

7.∫cos x dx = sin x +C .

8.∫sindx2 x = −ctg x +C .

9.∫cosdx2 x = tg x +C .

10.

∫

dx

=

1

arctg

x

+C .

a

2

2

a

+ x

a

11.

∫

dx

=arcsin

x

+C .

a

2

2

− x

a

∫

dx

x2 + a

+C .

12.

=ln

x +

2

x

+ a

13.

∫

ax +b

dx =

a

x

2

+cx + d

+

2b −ac

2x +c

+C ,

ln

arctg

x

2

+cx

+ d

2

4d

−c

2

4d −c

2

где D = c2 − 4d < 0 .

14.

In = ∫

dx

=

1

x

+

2n −3

In−1 +C ,

на-

(x2 + a2 )n

2n − 2

(x2 + a2 )n−1

2n − 2

зываемый рекуррентной формулой.

54

Искусство взятия интеграла заключается в том, что, используя свойства 1–7 и приведенные выше «табличные» интегралы, свести заданный интеграл к табличному.

Для интегралов определенного вида существуют процедуры, позволяющие выразить интегралы через элементарные функции. Приведем некоторые виды таких интегралов и соответствующие процедуры их взятия.

1. Интеграл от дробно-рациональной функции имеет вид

∫Pm (x)dx , Qn (x)

где Pm (x) , Qn (x) – многочлены степени m и n соответственно, m и n – натуральные числа.

2. Интеграл от тригонометрических функций имеет вид

∫Pm (sin x,cos x)dx , Qn (sin x,cos x)

где Pm x c (sinx) ,, osQn (sin x,cos x) – рациональные функции от функций sin x, cos x степени m и n соответственно, где m и n – натуральные числа

	3. Интеграл от иррациональности:
			ax +b
		Pm x,
			cx + d		dx ,
	∫		ax +b
		Qn x,
			cx + d

	ax + b						ax + b
где P x,				,	Q	x,			– рациональные функции от
m					n
	cx + d						cx + d
переменных x и			ax +b			степени m и n соответственно, где m и n –
			cx + d

натуральные числа, a, b, c, d – некоторые числа.

4.Интеграл Эйлера:

∫Pm (x, ax2 +bx + c )dx , Qn (x, ax2 +bx + c )

55

где Pm (x, ax2 +bx +c ),	Qn (x, ax2 +bx +c ) – рациональные
функции от переменных x и	ax2 + bx + c степени m и n соответст-

венно, где m и n – натуральные числа, a, b, c – некоторые числа, a ≠ 0 .

Для всех этих интегралов существуют стандартные подстановки, которые обязательно приведут к полному решению задачи, т.е. взятию интеграла. Конечно, этот путь может быть долог и изобиловать чисто техническими трудностями, и поэтому рекомендуем сначала посмотреть, не удастся ли взять интеграл другим способом.

Рассмотрим процедуры взятия приведенных видов интегралов. 1. Для взятия интеграла от дробно-рациональной функции

Pm (x) рекомендуем следующую схему решения, всегда приводя-

Qn (x)

щую к успеху:

1) если степень полинома в числителе больше или равна степени полинома в знаменателе, то путем деления приводим исходное

подынтегральное выражение к виду Tk (x) = Rl (x) , где степень

Qm (x)

многочлена Rl (x) меньше степени многочлена Qm (x) . Интеграл от полинома Tk (x) легко берется;

2) раскладываем знаменатель в произведение «простых» сомножителей по теореме Безу:

Qm (x) = (x − a1 ) ... (x −b1 )k1 ... (c1 x2 + d1x + e1 ) ...×

×(p1 x2 + r1 x + q1 ) l1 ...

Здесь a1 ,..., am – действительные корни полинома Qm (x) кратности

1,	b1 ,...,bn	–	действительные			корни	кратности k1 ,..., kn , скобки
(c x2 + d x +e ),...				отвечают паре комплексно-сопряженных корней
1	1	1
кратности		1,	а	скобки	( p x2	+ r x + q ),...		– паре комплексно-
					1	1	1

сопряженных корней кратности l1;

56

3) раскладываем дробь

Rl (x)

в сумму простых дробей вида:

Q (x)

m

A

+... +

B1,1

+

B1,2

+... +

B1,k

+... +

1

1

(x −b1 )k1

(x −b1 )k1

x − a1

−1

(x −b1 )

+

C + D x

+... +

C1,1 + D1,1x

C1,l

+ D1,l x

1

1

+... +

1

1

+...

c x

2

+ d x + e

( p x

2

+ r x + q )

l

( p x

2

+ r x + q )

1

1

1

1

1

1

1

1

1

1

Нетрудно заметить, что действительному корню кратности k1

отвечает

группа

слагаемых

B1,1

+

B1,2

+... +

B1,k1

и

(x −b1 )k1

(x −b1 )k1 −1

(x −b1 )

так до исчерпания показателя скобки знаменателя до единицы, а комплексным сопряженным корням, дающим в разложении Безу

скобку				( p x2		+ r x + q ) s			,	отвечает		группа	слагаемых
				1		1	1
	C1,1 + D1,1x					+... +	C1,l1		+ D1,l1 x		с показателем s, уменьшаю-
	( p x	2		l			( p x	2	+ r x + q )
			+ r x + q ) 1
1			1	1			1		1	1

щимся от l1 до 1. Постоянные в числителях суть произвольные, пока еще не определенные константы;

4) приводя к общему знаменателю всю полученную на предыдущем этапе группу слагаемых, приравниваем полученный числитель полиному Rl (x) . Настоятельно рекомендуется после приведе-

ния к общему знаменателю привести полученный числитель к стандартному виду многочлена a1xm−1 + a2 xm−2 +... + am ;

5)приравняем коэффициенты при одинаковых степенях xk и, таким образом, получим систему линейных алгебраических уравнений, которая всегда (!) имеет единственное решение (перед решением системы надо убедиться, что число уравнений в системе совпадает с числом неизвестных);

6)применим свойство «плюс-минус» (свойство 5) к заданному

интегралу и получим его представление через табличные интегралы;

7) добавляем к полученному решению произвольную постоянную C в случае неопределенного интеграла.

57

Интеграл от дробно-рациональной функции является основным в курсе математического анализа для студентов инженерных специальностей, так как любую функцию, встречающуюся на практике, можно с любой степенью точности аппроксимировать дробнорациональной функцией. Так как не имеет смысла достигать точности аппроксимации, большей, чем точность экспериментальных данных, то степени полиномов в числителе и знаменателе не вели-

ки, и взятие интеграла можно доверить ЭВМ.

2. Рассмотрим интеграл от тригонометрической функции

n

∑ ai,k sini x cosk x

∫	i,k =0	dx ,
	m

∑bi,k sini x cosk x

i,k =0

где {ai,k ;bi,k } – числа, а показатели степеней i и k – натуральные числа или нули.

x

Предлагается универсальная подстановка: t = tg 2 , позволяю-

щая преобразовать исходный интеграл в интеграл от некоторой дробно-рациональной функции, а последний мы уже умеем брать.

Стандартная подстановка гарантирует взятие интеграла, но зачастую полезно попытаться взять его по-иному.

3. Рассмотрим интеграл, который мы называем интегралом от иррациональности:

n

∫	∑ ai,k xi zk
	i,k =0	dx ,
	m
	∑bi,k xi zk
	i,k =0

где {ai,k ;bi,k } – числа, i, k – натуральные числа или нули. А пере-

менная z =	ax +b	. Из последнего выражения легко получить за-
	cx + d

висимость x от z, а далее поступать по инструкции и привести интеграл к переменной интегрирования z.

58

4. Рассмотрим интеграл Эйлера:

	n		+bx + c )	k
∫	∑ ai,k xi (	ax2
	i,k =0				dx .
	m		+bx + c )	k
	∑bi,k xi (	ax2
	i,k =0

Чтобы интеграл (неопределенный!) имел смысл, необходимо, чтобы подкоренное выражение на каком-нибудь промежутке было положительным. Это возможно в двух случаях: либо для всех x, либо уравнение ax2 + bx + c = 0 имеет два различных действительных корня. Эйлером предложены три стандартных замены, позволяющие превратить интеграл в интеграл от дробно-рациональной функции:

1) a > 0. В этом случае полагаем ax2 + bx + c =	ax + t . После
возведения в квадрат слагаемые с x2 исчезают, а переменная x вы-
ражается через переменную t дробно-линейным образом. Проводя
стандартные действия при указанной подстановке,	получим под

интегралом дробно-рациональную функцию;

2) c > 0. Полагаем ax2 +bx +c = xt + c и повторяем все действия п. 1).

3) пусть квадратный трехчлен ax2+bx+c имеет различные веще-

ственные корни λ и μ. Произведем замену ax2 +bx + c = t (x −λ) и

проделаем все необходимые действия.

В том случае, когда интегрируемая функция зависит от больше-

го числа аргументов, чем размерность области интегрирования, «лишние» аргументы называются параметрами, а сам интеграл –

интегралом, зависящим от параметров. Приведем только один пример такого интеграла:

b( y)

I = ∫ f (x, y)dx .

a( y)

Интеграл, рассматриваемый как функция от переменной (параметра) y, можно дифференцировать по этому параметру. Верхний и нижний пределы интегрирования могут также рассматриваться как

59

функции этого же параметра. Дифференцирование интеграла от параметра проводится по формуле Ньютона–Лейбница:

	dI		b( y)	∂		′	′
		=	∫		f (x, y)dx +	f (b( y), y) b ( y) −	f (a( y), y) a ( y) , (4.4)
	dy			∂y
			a( y)

если функция f(x, y) непрерывна и существует непрерывная производная f y′(x, y) в прямоугольнике [α,β, γ,δ], а также существуют производные a′( y) , b′( y) .

4.2. Примеры решения задач

Пример 4.1. Найти интеграл ∫x ln x dx .

Разберем подробно процесс нахождения алгоритма взятия данного интеграла.

Поскольку этот интеграл не относится к «табличным», то ответ написать сразу невозможно (конечно, если вы его не угадаете, но это – редкое качество). Замена переменных тоже не помогает свести интеграл к табличному (напоминаем, что это – наша цель). Остается попробовать взять интеграл по частям.

Если мы примем функцию x за u, а функцию ∫ln x dx за v (обо-

значения соответствуют обозначениям, использованным в седьмом свойстве интегралов), то нам придется для нахождения функции v

брать интеграл ∫ln x dx , который также не относится к «таблич-

ным», и работа по взятию интеграла затягивается. Попробуем вве-

сти другое обозначение – ∫x dx назовем функцией v, а ln x – функ-

цией u. Тогда функция v легко находится (интеграл ∫x dx относит-

ся к числу «табличных») и мы пишем формулу «взятия интеграла по частям»:

∫u dv =uv −∫vdu → ∫ln x d

x2

=

x2

ln x −∫

x2

dx

=

x2

ln x −∫

x

dx +C ,

x

2

2

2

2

2

и, окончательно ∫x ln x dx =

x2

ln x −

x2

+C .

2

4

60