Башуров Методика решения математических задач 2011

2

Рассмотрим определенный интеграл от этой функции x ln x dx .

1

Первым делом надо обратить внимание на то, чтобы подынтегральная функция была определена на всем промежутке интегрирования. В данном примере это условие выполнено, и поэтому

2	x	2		12	x	2			2		3
x lnx dx			lnx							2ln2		.
1	2		4						1	4

Пример 4.2. Требуется найти неопределенный интеграл

x 3

(x2 3x 2)(x 1)(x2 2 1)dx.

Под интегралом стоит дробно-рациональная функция, и поэтому процесс взятия в особом рассмотрении не нуждается – берем интеграл по «инструкции».

Поскольку степень многочлена в числителе меньше степени многочлена, стоящего в знаменателе, то необходимость деления числителя на знаменатель отпала.

Разложим знаменатель на произведение скобок, согласно тео-

реме Безу (x2 3x 2)(x 1)(x2 x 1) (x 2)(x 1)2(x2 2 1).

Каждой скобке в разложении отвечает простейшая дробь:

скобке (x – 2) отвечает дробь	A		,
	x 2
2				B			C
скобке (x – 1) отвечает сумма дробей								,
				(x 1)2			x 1
скобке (x2 + x + 1) отвечает дробь			Dx E		.
			x2 x 1

Числители всех дробей содержат произвольные, пока неопределенные, коэффициенты A, B, C, D, E

Итак, мы имеем разложение подынтегральной функции на простейшие дроби

x 3		A		B		C		Dx E	.
(x2 3x 2)(x 1)(x2 x 1)		x 2		(x 1)2
						x 1		x2 x 1

61

Приводя все дроби к общему знаменателю и, приравнивая коэффициенты в числителе при одинаковых степенях x, стоящих в левой и правой частях предыдущего равенства, получим систему для нахождения произвольных постоянных

A C D 0;
A B 2C 4D E 0;
	.
B 5D 4E 0;
A B C 2D 5E 1;
A 2B 2C 2E 3.

Подсчитав число уравнений и неизвестных, убеждаемся в том, что их число одинаково, и поэтому нет необходимости искать ошибки на предыдущих этапах решения.

Решаем систему и определяем все произвольные (до сей поры) постоянные

		5
	A			,
		7
				1
	B								,
				7
				1
								, .
	C
				3
							8
	D										,
				21
				1
	E									.
				7

Последний шаг состоит в том, что мы, используя «таблицу» интегралов, пишем окончательно ответ (не забывая о произвольной постоянной):

						x 3				dx
		(x2			3x 2)(x 1)(x2
								x 1)
		5			1	1			8x 3
											dx=
					7(x 1)2		3(x 1)		21(x2 x 1)
		7(x 2)

62

	=	5	ln		x −2			+	1 1				−		1		ln			x −1		−	4		ln			x2	+ x +1		+
									7 x −1
		7												3									21
		+				2				3arctg						1		(2x +1)					3			+C.
						63										3

Пример 4.3. Рассмотрим тригонометрический интеграл

1

∫sin2 x dx .

0

Если мы будем его брать по «инструкции», то придем к необходимости брать интеграл (№ 14 в списке табличных интегралов), который приводит к довольно длинной цепочке преобразований. В преобразованиях нет ничего страшного, но их количество повышает вероятность появления арифметической ошибки. Воспользуемся тем, что в тригонометрии есть множество формул, и одна из них годится для решения нашего примера.

	Так как	sin2 x =	1−cos 2x	,	то		наш интеграл превращается в
			2
	сумму двух «табличных» интегралов
		1			1					1
		∫sin2 x dx =		1	∫dx − 1					∫cos 2x dx
		0		2	0			2		0
	и ответ не представляет труда записать в виде
			1			1			1
			∫sin2 x dx =				−				sin 2 .
								4
			0		2

Используя этот путь, мы минуем этап «обратной» подстановки (в случае неопределенного интеграла), и нам нет необходимости отыскивать новые нижний и верхний пределы интегрирования (в случае определенного интеграла). (Читатели нас простят, что мы интеграл от косинуса двойного угла назвали «табличным».)

Проверка (этап 5 решения) заключается во взятии производной от «ответа» и в сравнении полученного выражения с исходным – они должны быть тождественны.

Пример 4.4. Найти производную интеграла от параметра

y2

∫tg (xy)dx .

y

63

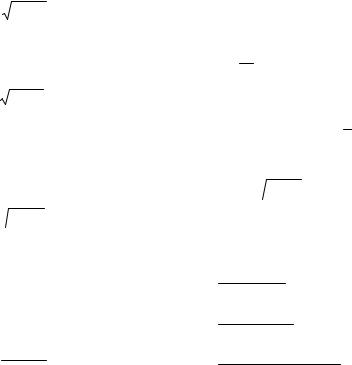
Поскольку параметром в данном примере служит переменная y, чисто формально применим для нахождения производной формулу Ньютона–Лейбница (4.4):

d	y2	y2		x			3		2
	∫tg (xy)dx = ∫					dx + tg ( y		) 2 y − tg ( y		) 1 .
dy			cos	2	(xy)
	y	y

4.3. Задачи для самостоятельного решения

Найти сначала неопределенный интеграл, а в задачах с указан-

b

ными значениями a и b вычислить определенный ∫ f (x) dx :

a

4.1.	∫	x2 −1			dx , a=1, b=2.
		x	3
4.2.	∫	ln(ln x)				dx , a=1, b=e.
		x
4.3.	∫	1−2xdx , a= –1, b=0.
4.4.	∫	ln2 x		dx .
		x

4.5.∫sin x cos 2x dx , a=0, b=π.

4.6.∫sin2 x cos3 x dx .

4.7.∫ x +1 x dx , a=0, b=3.

4.8.∫cos3 x dx .

4.9.∫(cos2 x +sin5 x)dx .

4.10.∫ x(6x −5)10dx .

4.11.∫ x3 ln(x4 )dx .

x4

4.12.∫ x3 + 27 dx , a= –2, b=0.

4.13.∫arctg x dx .

4.14.∫ x arcsin x dx .

4.15.∫ x3 ln(x +1)dx .

−x

4.16.∫ x2e 5 dx .

4.17.∫ x cos 2x dx .

4.18.∫e3x cos x dx , a=0, b= π2 .

4.19.∫ xex sin x dx .

4.20.∫ln x + 1+ x2 dx .

4.21.∫ln(sin x)ctg x dx .

4.22.∫ln(sin x)tg x dx .

x−1

4.23.∫ x2 − 5x + 6 dx .

2x + 3

4.24. ∫ x3 + x2 − 2x dx .

x

4.25. ∫(x2 − 3x −10)(x + 2) dx .

64

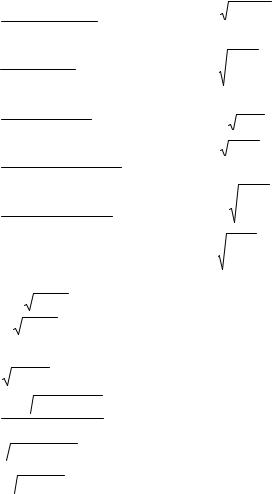
x3 −8

4.26. ∫ x3 + 2x2 + x + 2 dx .

4.27. ∫ (x2 +x)(1−x)dx , a= 1, b=2. (x2 +1)(x+2)

x5

4.28.∫(x2 +1)(x2 −1) dx .

x2 +1

4.29.∫(x3 −1)(x2 − 7x + 6) dx .

x4

4.30.∫(x2 + x +1)(x2 −1) dx .

	4.31.	∫ctg x +				x3 (x2 −5x +4)		dx .
					(x2 −		4x +3)(x −1)3
	4.32.	∫	x +	x2 −1			dx .
				x2 −1
	4.33.	∫	x2			dx , a= –1, b=0.
			4 − x2

4.34.∫ x + − x2 − x +1 dx .

1+ x

4.35.∫ x2 + 2x + 4 dx .

4.36.∫x − x2 +1 dx .

4.37. ∫

4x2 −1

dx , a= 1, b=3.

x

4.38. ∫

x +1

1

dx .

2

x

x

4.39. ∫

x +1

dx .

x

x −1

4.40. ∫

x + 5

dx , a= 2, b=5.

x

4.41. ∫

1

x3

dx .

x

x +1

4.42. ∫

x

(x −1)dx .

x +1

4.43. ∫

dx

.

2 + sin x

4.44. ∫

sin 2 x + cos x

dx .

tg x

4.45. ∫

3sin x

dx .

1 − sin x

4.46. ∫

cos x

dx .

2 + cos x

4.47. ∫

5

dx .

8

− 4sin x

+ 7cos x

Найти производную по параметру:

	3		α2
4.1	∫cos2 ln(x ctg y)dx .	4.3	∫sin4 (α x + α) dx .
	2		eα
	y2		eα
4.2	∫ xyex2 y dx .	4.4	∫	sin(α x2 )dx .
	cos y		α3 +α2 +α+1

65

	x cos x
4.5	∫		x2 y2xy dy .
	1−x2
	eα −α3
4.6	∫ cos(α2β3 )dβ.
	α3 −eα
	ex2		x+y
4.7	∫ e	x2 +y2		dy .

e−x

xx

4.8∫ sin(xy) dy .

2ln x

ctg(αeα )

4.9 ∫ cos(αβ3 ) dβ.

tg α

1α

4.10∫cos2 (αx)dx + ∫cos3 (αx2 )dx.

α−1

xsin x

4.11 ∫ x2 yexy dy.

x2

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1 Архипов Г.И., Садовничий В.А., Чубариков В.Н. Лекции по математическому анализу. М.: Высшая школа, 1999.

2. Фихтенгольц Г.М. Основы математического анализа. Т. 1. СПб.:

Лань, 2006.

3 Фихтенгольц Г.М. Основы математического анализа. Т. 2. СПб.:

Лань, 2006.

4.Пискунов Н.С. Дифференциальное и интегральное исчисления. Т.1. М.: Физматлит, 1985.

5.Пискунов Н.С. Дифференциальное и интегральное исчисления. Т.2. М.: Физматлит, 1972.

66

Глава 5. КРАТНЫЕ ИНТЕГРАЛЫ

5.1. Определения, основные теоремы и формулы

Кратные интегралы имеют вид:

∫∫...∫ f (x1 , x2 ,..., xn )dx1dx2 ...dxn или	∫...∫ f (M )dV ,
V	V

где размерность области интегрирования V определяется количеством аргументов у функции f(x1,x2,…,xn). Все свойства кратных интегралов аналогичны соответствующим свойствам определенного интеграла.

Выделим только одно: если область интегрирования V представима в виде объединения пересекающихся только по границам подобластей {V k}, то

∫...∫	f (M )dV = ∑∫...∫ f (M )dV .
V	k Vk

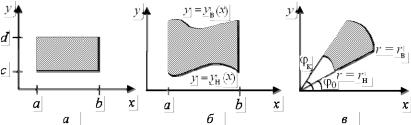
Взятие двойных интегралов можно проводить по следующей схеме. Рассматривается сначала область интегрирования и выясняется, к какому из трех типов (рис 5.1) принадлежит область интегрирования.

Рис. 5.1

1. Область V относится к первому типу (рис. 5.1, а). В этом случае используется формула, называемая «формулой повторного интегрирования»:

	f (x, y)dxdy =	b d		d b		(5.1)
∫∫			f (x, y)dy dx =		f (x, y)dx dy .
		∫ ∫		∫ ∫
V		a c		c a

67

2. Область V относится ко второму типу (рис. 5.1, б). В этом случае искомый интеграл вычисляется по формуле

	b yв (x)
∫∫ f (x, y)dxdy = ∫ ∫		f (x, y)dy dx .	(5.2)
V	a yн (x)

Замечание. Если для областей первого типа не важен порядок интегралов, то менять порядок интегрирования для областей второго типа чисто механически нельзя!

3. Область V относится к третьему типу (рис. 5.1, в). В этом

случае рекомендуется сделать переход к полярным координатам x = r cos ϕ, y = r sin ϕ и применить формулу

∫∫ f (x, y)dxdy =∫∫ f (r cos ϕ, r sin ϕ)r drdϕ.		(5.3)
V	V

Область интегрирования V* относится к первому типу (см. рис. 5.1, а).

Взятие тройных интегралов происходит по аналогичной схеме.

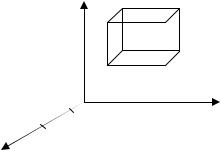
1. Если область интегрирования имеет вид прямого параллелепипеда (рис. 5.2), то

то

f (x, y, z)dxdydz =

b d g

(5.4)

∫∫∫

f (x, y, z)dz dy dx .

∫

∫ ∫

V

a c e

z

g

e

a	b					y
	c			d
x						Рис. 5.2

2. Если область интегрирования можно представить в виде, изображенном на рис. 5.3, где уравнения нижней и верхней «граней» соответственно z = zн(x,y) и z = zв(x,y), то

68

	zв (x, y)
∫∫∫ f (x, y, z)dxdydz = ∫∫ ∫
V	S zн (x, y)

z

f (x, y, z)dz dxdy . (5.5)

y

x

Рис. 5.3

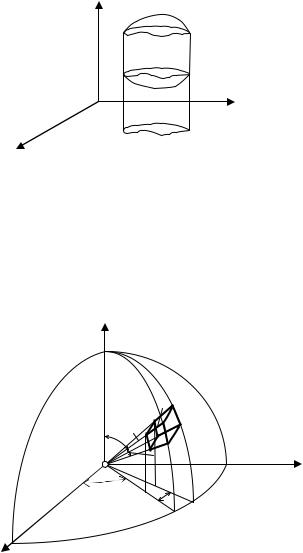
3. Если область интегрирования представима в виде, представленным рис. 5.4, то

∫∫∫ f (x, y, z)dxdydz =

V

r1 θ1 ϕ1

= ∫ ∫ ∫ f (r cos θsin ϕ, r sin

r0 θ0 ϕ0

z

θsin ϕ, r cos θ)r
	2	sin θdϕdθ
			dr . (5.6)

	dr
	C
θ	r
0	dθ
	y

ϕ

dϕ

x

Рис. 5.4

69

Поскольку в курсах высшей математики для инженерных специальностей ограничиваются обычно двойными и тройными интегралами, то мы приведем только формулу для вычисления кратных интегралов ∫…∫ f (x1, x2 ,..., xn )dx1dx2 ...dxn при замене переменных

V

x1 = ϕ1 (ξ1,...,ξn ),........................... .

xn = ϕn (ξ1,...,ξn ).

Эта формула имеет вид:

∫...∫ f (x1, x2 ,..., xn )dx1dx2 ...dxn =

V

= ∫...∫ f (ϕ1 (ξ1, ...,ξn ),...,ϕ2 (ξ1,...,ξn )) J dξ1...dξn ,

V

где V* – область, в которую перешла исходная область интегрирования при указанной замене, а J, называемый «якобианом преобразования», вычисляется по формуле:

∂ϕ1

∂ϕ1

...

∂ϕ1

∂ξ1

∂ξn

∂ξ2

∂ϕ2

∂ϕ2

...

∂ϕ2

J =

∂ξn

.

(5.7)

∂ξ1

∂ξ2

..........................

∂ϕn

∂ϕn

...

∂ϕn

∂ξn

∂ξ1

∂ξ2

5.2. Примеры решения задач

Пример 5.1.	Найти двойной интеграл по области D:
{0 ≤ x ≤1;1 ≤ y ≤ 2}	∫∫xsin(xy) dx dy .
	D

Поскольку область интегрирования относится к первому типу (см. рис. 5.1, а), то мы вправе выбирать любой порядок интегрирования. Однако если мы представим двойной интеграл в виде

70