Башуров Методика решения математических задач 2011

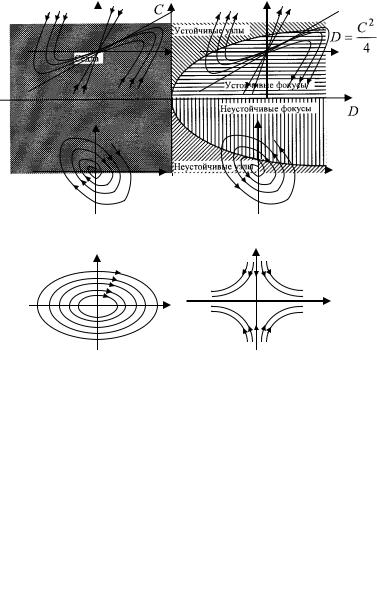
y

y

y

y

аб

y	y
y	y

вг

y

y
y	y
д	е

Рис. 10.2

На рис. 10.3 изобразим области «устойчивых» параметров системы (10.22) и «неустойчивых». Стрелочки на рисунке указывают направление изменения переменных x и y.

Рис. 10.3

131

10.2. Примеры решения задач

Пример 10.1. Решить уравнение 2x2dy = (x2 + y2 )dx .

Перепишем уравнение в виде 2y′ =1		y		2
	+			, полагая x ≠ 0 .
	x

Данное уравнение имеет вид (10.4), т.е. является однородным. По-

y

′

′

ложив в нем u = x

и y

= xu

+u , получим уравнение с разделяю-

′

2

du

2

щимися

переменными

2xu

+ 2u =

1+u ;

2x dx = u

−2u +1;

2du

= dx ,

u ≠1 .

Интегрируя и подставляя

y

вместо u, полу-

(u −1)2

x

x

чим первым интеграл исходного уравнения:

2

2

−2 x

−

= ln

x

+ln

C

;

−

= ln

Cx

;

Cx= e

y−x

.

u −1

y

−1

x

При разделении переменных мы делили на х и на (u −1)2 . Не-

посредственной проверкой легко убедиться, что х = 0 и u = 1, т.е. y = x, являются также решениями данного уравнения, но они не входят в общий интеграл.

Пример 10.2. Решить уравнение y′−2xy = 2xex2 .

Данное уравнение имеет вид (10.5), следовательно, является линейным дифференциальным уравнением первого порядка. Соот-

ветствующее однородное уравнение есть y′− 2xy = 0 . Разделяем
переменные	dy	= 2xdx , y ≠ 0 , получим y = Cex2 . Заменяем произ-
	y

вольную постоянную С на функцию С(x), т.е.			y = C(x) ex 2				. Подста-
вим y = C(x) e	x2	′		x2	= 2x e	x2		, откуда
		в исходное уравнение: C (x) e

C(x) = x2 +C1 . Следовательно, общее решение данного уравнения имеет вид y = (x2 +C1) ex 2 .

132

Непосредственной проверкой убеждаемся, что y = 0 не является решением нашего уравнения.

Пример 10.3. Найти общее решение уравнения y′′ + y′− 2y =1. «Справочным бюро», как всегда, служит первый параграф дан-

ной главы.

Уравнение линейное неоднородное, с постоянными коэффициентами, и поэтому сначала ищем общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами. Решаем характеристическое уравнение

λ2 + λ – 2 = 0, его корни λ1 = 1, λ2 = –2.

Общее решение уравнения при таких корнях, согласно «справочному бюро», имеет вид y(x) = С1ex + С2e-2x.

Будем считать, что произвольные постоянные С1 и С2 зависят от x, и найденное общее решение подставим в исходное уравнение.

Для

этого

сначала

найдем

первую

производную

′

x

−2C2e

−2 x

′

x

′

−2 x

)

и приравняем нулю вторую

y (x) = (C1e

) +(C1e

+C2e

скобку

′

x

′

−2 x

= 0 .

(*)

C1e

+C2e

Вторая производная с учетом, что вторая скобка равна тождест-

′′

x

+ 4C2e

−2x

′ x

′

−2x

) .

венно нулю, есть y (x) = (C1e

) +(C1e

−2C2e

Вновь приравняем вторую скобку, но уже к единице

′

x

′

−2x

=1.

(**)

C1e

−2C2e

Решим систему, составленную из уравнений (*) и (**), относительно C1′ и C2′ :

C ex +C′e−2 x = 0,

1 2

C1′ex − 2C2′e−2 x =1.

Решение системы имеет вид C1′ = 13 e−x , C2′ = −13 e2 x . Интегри-

руя, получим C1

= −

1

e

−x

~

, C2

= −

1

e

2 x

~

~

~

– «ис-

3

+C1

6

+C2

, где C1

и C2

тинные» произвольные постоянные, и решение исходного уравнения имеет вид

133

y(x)=e

x

1

e

−x

~

-2x

(−

1

e

2 x

~

(−

3

+C1) +e

6

+C2 ) .

dy1

= 3y

+ 2y

2

+3e2 x ,

1

Пример10.4. Решить систему уравнений dx

dy2

= y1 + 2 y2 + e

2 x

.

dx

Данная система является линейной неоднородной с постоянными коэффициентами. Сначала найдем решение однородной системы

					dy1	= 3y + 2y		2	,
							1
											(*)
					dx
					dy2	= y1 + 2y2.
					dx
	Составляем				и решаем		характеристическое уравнение
	3 −λ	2		=0,	λ2 −5λ + 4 =		0 , λ = 4 , λ			2	=1.
	1	2 −λ					1
	Для простого корня λ1 = 4						находим собственный вектор (α, β),

−α + 2β = 0,

решаем систему и получаем α = 2β. Значит, вектор

α − 2β = 0

(2, 1) – собственный, и y1 = 2e4 x , y2 = e4 x – частное решение системы (*).

Для простого корня λ2 =1 находим собственный вектор (1, –1) и частное решение y1 = ex , y2 = −ex .

y 0 (x) = 2C e4x +C						ex ,
	1		1		2			(**)
		0		4 x			x
			(x) = C1e		−C2e
y2

– решение однородной системы. Чтобы найти С1 и С2, подставим (**) в исходную систему:

2C ′e4 x

+C ′ex

= 3e2 x ,

′

x

3x

′

4

−2 x

1

2

−2C1′ e

−C ′ex

C2

= 3e

,

C1

=

e

.

= e2 x ,

3

C ′e4 x

1

2

Находим

134

2

−2x

~

x

8

x

~

C1

= −

e

+C1

,

C2 = 3e

−

e

+C2 .

3

3

Тогда общее решение неоднородной системы будет иметь вид

y

~

4 x

~

e

x

−e

2 x

(x) = 2C e

+C

1

~

1

~

2

2 x .

4 x

x

−e

y2 (x) = C1e

−C2e

Пример 10.5. Рассмотреть поведение решения в окрестности

dydt = ln(1+ y) +ln(1+ x),

точки покоя для системы

dxdt = 2x −3y.

Точке покоя отвечают значения x = 0 и y = 0. Разложим в ряд Тейлора в окрестности точки (0,0) правые части уравнений исходной системы, оставив только первые слагаемые, и разделим одно уравнение на другое, приводя систему к виду, рассмотренному в этой главе. Получим a = 1, b = 1, c = 2, d = –3.

Найдем параметры С = 2 и B = –5 и обратимся вновь к «справочному бюро». Рис. 10.2, a дает представление о поведении реше-

ния в окрестности точки покоя (0,0).

10.3. Задачи для самостоятельного решения

Найти общие решения уравнений первого порядка:

10.1.x2 + xy′ = 3x + y′.

10.2.y′(3x2 − 2x) − y(6x − 2) = 0 .

10.3.y′ = (x − y)2 +1.

10.4.(x − y +3)dx + (3x + y +1)dy = 0 .

10.5.(2 y2 − xy)dx + (xy − x2 − y2 )dy = 0 .

10.6.x + y − 2 + (1− x) y′ = 0 .

10.7. y	′	=	xsin x − 2xyex2	.
			ex2

135

10.8.

y′

=

1

.

2x − y2

10.9.

(2x −1) y

′

− 2 y =

1− 4x

.

x2

10.10.

xsin x y′+ (sin x − xcos x) y = sin x cos x − x .

10.11.

y

′

=

x3 −3xy2

3x2 y − y3 .

6x2 +

4 y2 −5xy

10.12.

y′

=

.

y2 −8xy +

5 x2

2

10.13.

3x2eydx + (x3ey −1)dy = 0 .

x

1

1

y

1

x

dx

dy = 0 .

10.14.

+

+

+

+

+

2

2

2

2

2

x

+ y

x y

x

+ y

y

y

10.15.

1+ xy

dx +

1− xy

dy = 0 .

x2 y

xy2

1

1

10.16.

sin y + ysin x +

dx + xcos y −cos x +

dy = 0 .

x

y

10.17.

y = y′2ey′ .

y′

10.18.y′ = e y .

10.19.x = ln y′+sin y′ .

10.20.x = y′2 + 2 − 2 y′.

10.21.x( y′2 −1) = 2 y′.

1

10.22. xy′2 = e y′ .

Понизив порядок данных уравнений, свести их к уравнениям первого порядка:

10.23.y′′′+3y′′+ 2 y′ =1− x2 .

10.24.y(4) + 2 y′′′+ y′′ = x2 + x −1 .

136

10.25.y′′(ex +1) + y′ = 0 .

10.26.y′′′y′ = 2 y′′2 .

10.27.5y′′′2 −3y′′y(4) = 0 .

10.28.x2 yy′′+ y′2 = 0 .

10.29. y′′+	y′		y		y′2
		+		=		.
	x		x2		y

Решить уравнения:

10.30.y′′+ y = sin1 x .

10.31.y′′−3y′+ 2 y = sin x .

10.32.y′′− y = ex cos2 x .

10.33.y′′−5y′ = 3x2 +sin 5x .

10.34.y′′− y = ex cos2 x .

10.35.y′′+ 2 y′+ 2 y = ex sin1 x .

10.36.y′′+ 2 y′+ y = 3e−x x +1 .

10.37.y′′+ 4 y′+ 4 y = e−2 x ln x .

Найти решения, удовлетворяющие заданным начальным условиям:

10.38.y′− 2x −5 y = 5 , y(2) = 5.

x2

10.39. y′+ y tg x = cos	2		π				1
		x ,	y			=		.
				4			2

2

10.40.y2dx +(x +e y )dy = 0 , y(e) = 2.

10.41.(x cos2 y − y2 ) y′ = y cos2 y , y(π) = π4 .

10.42.y′+ 4x3 y = 4(x3 +1)e−4x y2 , y(0) = 1.

10.43.2y′+ y cos x = y−1 cos x(1+sin x) , y(0) = 1.

137

4y

3

y

′′

= y

4

−1 , y(0) =

′

1

10.44.

(0) =

2

2 .

2, y

10.45. y

′′

+8sin y cos

3

y

′

= 0 , y(0) = 0, y (0) = 2 .

10.46. y

3

y

′′

+ 49 = 0 ,

′

y(3) = −7, y (3) = −1 .

10.47. x

2

y

′′

−3xy

′

=

6 y2

− 4 y , y(1)

′

x2

=1, y

(1) = 4 .

10.48.

y

′′′

= 3yy

,

y(0) = −2, y (0) = 0, y (0) = 4,5 .

′

′

′′

10.49.

y

′′

+3y

′

=

9e3x

,

′

1+ e3x

y(0) = ln 4, y (0) = 3(1−ln 2) .

y′′+ 4 y =8ctg 2x

π

π

10.50.

,

y

= 5, y′

= 4 .

4

4

′′

π2

y(0)

′

10.51.

y

+ πy = cos πx ,

= 3, y (0) = 0 .

10.52.

y

−6 y

+

8y = 2 + e−2 x

, y(0) =1+3ln3, y (0) =10ln3 .

′′

′

4

′

10.53.

y

+9 y = cos3x ,

y(0) =1, y (0) = 0 .

′′

9

′

4

π

π

10.54.

y′′

+ 4 y =

,

y

= 2,

y′

= π.

sin 2x

4

4

ex

10.55. y′′−3y′+ 2 y = 1+ e−x , y(0) =1, y′(0) = 0 .

Решить системы уравнений:

10.56.y1′ = 4 y1 + 6 y2 ,

y2′ = 4 y1 + 2 y2 .

10.57.y1′ = −5y1 − 4 y2 ,

y2′ = −2 y1 −3y2 .

10.58.y1′ = −7 y1 +5y2 ,

y2′ = 4 y1 −8y2 .

138

10.59.y1′ = y2 − 2 y1 −e2 x ,

y2′ = 2 y2 −3y1 + 6e2 x .

	y′		= y	,
10.60.		1	2		1
	y2′		= −y1 +			.
					cos x

10.61.y1′ = y1 + y2 −cos x,

y2′ = −2 y1 − y2 + cos x +sin x.

							2
	y1′	= −4 y1 − 2 y2 +							,
					e	x	−	1
10.62.
					3
	y2′	= 6 y1 +3y2	−					.
				e	x	−1

Найти решения уравнений, удовлетворяющие указанным краевым условиям при помощи пакета MathCAD:

10.63. y′′− y = 2x , y(0) = 0, y(1) = −1.

10.64.y′′+ y =1 , y(0) = 0, y π = 0 .

2

10.65.y′′+ y = 2x − π , y(0) = 0, y(π) = 0 .

10.66.	y′′		+ y =1 , y(0) = 0,			y(π) = 0 .
10.67.	y	′′	− y	′	− 2 y = 0 , y(+∞) = 0, y (0) = 2 .
						′

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1.Федорюк М.В. Обыкновенные дифференциальные уравнения. М.:

Наука, 1980.

2.Мышкис А.Д. Прикладная математика для инженеров. М.: Физматлит, 2007.

3.Карлов Н.В., Кириченко Н.А. Колебания, волны, структуры. М.: Физматлит, 2003.

4.Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М.: Наука, 1971.

5.Степанов В.В. Курс дифференциальных уравнений. М.: Наука,

1962.

139

Владимир Витальевич Башуров,

Инга Анатольевна Комлева

МЕТОДИКА РЕШЕНИЯ МАТЕМАТИЧЕСКИХ ЗАДАЧ

Редактор Е.Н. Кочубей

Макет подготовлен к печати Е.Н. Кочубей

Подписано в печать 15.12.2010.		Формат 60 84 1/16
Объем 7,75 п.л.	Уч.-изд. л. 7,75.	Тираж 100 экз.
Изд. № 9/1/18.		Заказ № 49.

Национальный исследовательский ядерный университет «МИФИ». 115409, Москва, Каширское шоссе, 31.

ООО «Полиграфический комплекс «Курчатовский». 144000, Московская область, г. Электросталь, ул. Красная, д. 42