Башуров Методика решения математических задач 2011

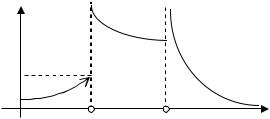
роннего предела» («предела слева», обозначаемого lim			f (x) , и
		x x0 0
«предела справа», обозначаемого lim		f (x) ).
	x x0 0
Определение 2.4. Для непрерывной функции имеет место сле-
дующее равенство:
lim f (x)	lim f (x)	lim f (x) f (x0).	(2.1)
x x0	x x0 0	x x0 0

Если функция непрерывна во всех точках некоторого множества (например, сегмента или интервала), то мы будем просто называть ее непрерывной на этом множестве. Если функция непрерывна на множестве своего определения, то такую функцию будем называть просто непрерывной.

В том случае, когда в некоторой точке «правый предел» не равен «левому», но они оба существуют, то такая точка называется «точкой разрыва первого рода». В случае, когда хотя бы один предел в точке x0 не существует (например, «равен бесконечности»), то такая точка называется «точкой разрыва второго рода». Рис. 2.1 иллюстрирует эти определения. Точка x = 1 – точка разрыва первого рода, точка x = 2 – точка разрыва второго рода.

y

2

1

1

2

x

Рис. 2.1

Некоторые функции традиционно носят название простейших элементарных функций. К ним относятся функции С, х , loga x, ax , sinx, cosx, arcsinx, arccosx.

Функции, которые получаются из простейших при помощи конечного числа операций сложения, вычитания, умножения, деления и суперпозиции, называются элементарными. Элементарные

21

функции на области своего определения непрерывны и дифференцируемы. Понятие дифференцируемости подробно рассмотрим в следующей главе.

В качестве примера приведем функцию вида f (x) Pn(x) , где

Qm(x)

Pn(x) и Qm(x) – полиномы соответственно степени n и m, которая носит название дробно-рациональной.

Замечание. Понятия «элементарная» или «неэлементарная» функции привязаны к промежутку, на котором она рассматривается. Так, функция y=|x| на промежутке [–1,1] является неэлементарной, а на промежутке [0,1] – элементарной.

Функция считается заданной явно, если ее удается записать в виде y = f (x) или y = φ(x). Если этого сделать не удается, то функция называется неявной. Пример явных функций: y = x, y = sin x. Пример неявной функции: x2 + y2 = 1.

Для непрерывных функций справедливы следующие теоремы. Теорема 2.1. Предел суммы, разности и произведения функций f (x) и φ(x), имеющих предел в точке x0, равен соответственно сум-

ме, разности и произведению пределов функций f (x) и φ(x) в этой же точке.

Записать эту теорему можно следующим образом:

lim f (x) (x) lim		f (x) lim (x);
x x0	x x0	x x0
lim f (x) (x) lim		f (x)lim (x).
x x0	x x0	x x0

Теорема 2.2. Предел отношения двух функций f (x) и φ(x) в точке x0 равен отношению пределов этих функций в указанной точке, если они существуют, и предел функции φ(x), стоящей в знаменателе выражения, задающего функцию, не равен нулю.

Запись этой теоремы выглядит так:

	f (x)		lim f (x)
lim			x x0	.
			lim (x)
x x0 (x)
			x x0

Теорема 2.3. Предел суперпозиции двух элементарных функций f (x) и φ(x) в точке x0, f (x) , в том случае, если значение φ(x0)

принадлежит области определения функции f(x), равен f (x0) .

22

Указанные теоремы являются основными при решении задач на нахождение пределов.

Функция f (x) называется бесконечно малой в точке x0, если

lim f (x) 0.

x x0

Рассмотрим отношение двух бесконечно малых в одной и той

же точке x0 функций α(x) и β(x) и найдем предел отношения (x) в

(x)

точке x0. Воспользоваться для нахождения предела теоремой 2.2 не представляется возможным из-за равенства нулю предела функции, стоящей в знаменателе. В этом случае возможны следующие ситуации:

1.Предел существует и равен нулю. В этом случае говорят, что функция α(x) имеет более высокий порядок малости по отношению

кфункции β(x) и это обстоятельство обозначают α(x) = o(β(x)). Также говорят, что функция β(x) имеет меньший порядок малости по сравнению с α(x).

2.Предел существует и равен конечному числу a ≠ 1. В этом случае говорят, что функции имеют один порядок малости и это обозначают α(x) = O(β(x)).

3.В случае, когда предел существует и равен единице, бесконечно малые функции называют эквивалентными (напоминаем, что речь идет только о точке x0).

В задачах, в которых требуется найти пределы функций, часто приходится «раскрывать» неопределенности какого-либо вида. Зачастую в таких задачах полезно одну бесконечно малую функцию заменять другой, эквивалентной первой, бесконечно малой функцией.

Примеры эквивалентных функций при x 0:	sinax			и ax, tgax
и ax,arcsinax и ax, arctgax и ax, 1 cosax и	ax 2		,	ln 1 ax и
	2

ax, eax 1 и ax. Часть приведенных примеров эквивалентных бесконечно малых в точке x=0 функций носит название «замечательный предел».

23

Перейдем к функциям двух и более переменных. Нам потребуются сейчас только понятия явной и неявной функций.

Если какая-то переменная выражается через остальные переменные в виде xk = f (x1, x2, …, xk-1, xk+1, …, xn) то перед нами явная функция n–1 переменных.

Если зависимость между переменными x1, x2, …, xn задана соотношением φ(x1, x2, …, xn) = 0, и это соотношение не удается записать в виде xk = f (x1, x2, …, xk-1, xk+1, …, xn), то перед нами, возможно, неявная функция. Область ее определения (и даже существования) зависит от точки, в которой рассматривается соотношение φ(x1, x2, …, xn) = 0. При этом, решая вопрос о существовании неявной функции, а в дальнейшем – и вопросы нахождения частных производных неявной функции, сначала следует обратить внимание на то, имеет ли смысл сама функция φ(x1, x2, …, xn) = 0 в этой точке.

2.2. Примеры решения задач

Пример 2.1. Найти предел функции f (x) sin(ln x) при x 1.

Здесь «справочным бюро» является п. 2.1.

Поскольку данная функция элементарна и точка x = 1 принадлежит области определения функции ln x, значение которой в этом аргументе принадлежит области определения функции sinx, то предел функции, в силу непрерывности элементарных функций, равен значению функции в точке x = 1, т.е. lim sin(ln x) 0.

x 1

Проверка заключается в простом повторении вычислений.

							, x 1,0 ,
			1 x
Пример 2.2. Задана функция:	1 x2					, x 0,1 ,
	f (x)
		1 x
			ln x						3
								, x 1,		.
									2
	cos					x
				2
24

Требуется найти предел в точках x 1 , x = 1, x = –2. 2

Сначала проверим, а принадлежат ли указанные точки области определения функции? Видно, что третья точка x = –2 не входит в область определения заданной функции, поэтому в дальнейшем

рассмотрим только две точки: x 1 , x = 1. 2

Точка x 1 принадлежит к области аргумента, на которой

2

функция элементарна, поэтому логично воспользоваться теоре-

мой 2.2. Поскольку предел знаменателя в точке x 1 не равен ну- 2

лю, то

					lim 1 x2
		1 x2			x	1				5
lim					2							.
			1 x		lim 1 x
1										6
x							1
2					x
					2

В точке x = 1 функция неэлементарная, и поэтому в этой точке рассмотрим два предела (слева и справа). Для нахождения предела

1 x2

слева воспользуемся тем,

что функция

элементарна, и по-

1 x

1 x2

этому предел

равен значению данной функции в точке

1 x

xlim1 0

x = 1, т.е.

1 x2

lim

1. Для нахождения предела справа прихо-

x 1 0 1 x

lnx

дится искать предел

lim

, но применение теоремы 2.2 при-

x 1 0 cos

x

2

водит к неопределенности

0

.

Раскроем эту

неопределенность.

0

Пусть x = 1 + z и z стремится к нулю. В силу эквивалентности бес-

25

конечно малых функций (в точке z = 0) ln(1 + z) и z заменим ln(1 + z) функцией z. Знаменатель по формулам тригонометрии можно заменить «синусом» а последний в точке 0 эквивалентен функции

z . Полученная дробь легко дает предел справа, и он равен

	2		2
	lim	f (x)			.
	x 1 0
	Поскольку предел в точке x = 1 слева не равен пределу справа,
	то отсюда следует вывод: в точке x = 1 предела нет.
			2x2, x , 1 ,
			x, x 1,0 ,
	Пример 2.3. Дана функция
		f (x) sin					,x 0,1 ,
						x
			sin(x 1)					, x 1, .
			(x 1)2

Найти точки разрыва и классифицировать их.

Поскольку элементарные функции на своих областях определения непрерывны, то ищем точки, в которых функция не является элементарной. Таких точек у заданной функции три: x1 = –1, x2 = 0, x3 = 1.

Рассмотрим их по очереди, учитывая, что в каждой такой точке необходимо искать односторонние пределы.

По сути, это является этапом 3 решения задачи. Правда, при нахождении односторонних пределов требуется выбрать способ его нахождения (это, как правило, раскрытие неопределенностей при помощи замены одной бесконечно малой величины другой или использование графика, построение графика будет подробно описано в гл. 3).

Рассмотрим точку x1 = –1. В этой точке lim 2x2 2, так как

	2х2	x 1 0
функция		элементарна на промежутке ( , ), и
lim f (x)	lim	( x) 1 по той же самой причине. Оба односто-
x 1 0	x 1 0

ронних предела существуют, но они не равны. Следовательно, точка x1 = –1 является точкой разрыва первого рода.

26

sin2 x

Рассмотрим точку x = 0. Предел слева находится легко и равен значению функции –x в точке x = 0. Для нахождения предела спра-

ва лучше всего нарисовать график функции sin и увидеть, что x

при стремлении x к нулю справа функция sin «бесконечное» x

число раз пересекает ось абсцисс и колеблется между +1 и –1. Следовательно, предела справа не существует и, стало быть, перед нами точка разрыва второго рода.

Обратимся к третьей точке x = 1. Предел слева lim f (x) равен

x 1 0

значению элементарной функции sin в точке 1, т.е. 0. Для нахо-

		x
ждения		предела справа заметим, что при x 1 отношение
	sin(x 1)	стремится к единице, а оставшийся множитель		1
	(x 1)		(x 1)
при x 1 0 стремится к «бесконечности». Следовательно,				пре-

дела справа не существует, и точка x = –1 является точкой разрыва второго рода.

Выполнение этапа 5 решения задачи (проверка) сводится к построению графика исходной функции и сравнению ее с полученным ответом. Как строить графики, мы подробно расскажем в следующей главе.

2.3. Задачи для самостоятельного решения

Найти пределы функций:

		sin x2 2
2.1. lim							.
		ln		2x 3
x 2
	tg(x		2	sinx)		3
2.3.lim					1	x			.
								x
x 0		x3 2x2

	tg(				x2)
2.2. lim		2					.
x 0
	cos			x 1
		2

2.4. limex e x 2 .

x 0

27

2.5.

lim

sin(tg x3)

.

2.6. lim

ln 28 3x2

x 3

.

3

1 cos

2 x

5x

x

x 3

2

x 0

x

3

3

2

2

x

2x2 3

1

4x

(3x

4x 1) 1

2.7.

lim

1

.

2.8.lim

x

.

x 4 x2

x

x

1 x2

6

x

x

(x2 7x 12) 1

x2

2.9. lim

.

lnx2 5x

2 x

x

sin ln 1 x2

2.10. lim

f x ?, если

f x

,x 0,

x

x 0

x 0.

1,

ln 1 x2

2.11. lim

f x ?, если

f x

,x 0,

x

x 0

x 0.

3,

xtgx

,x 0,

2.12. lim

f x ?,

lim f x ?, если

f x

1 cosx

x 0

x 1

x 0.

2,

Какие из следующих пар функций являются функциями одного порядка:

2.13.f (x) x3 x2 x 1, g(x) x3 x при x 1.

2.14.f (x) xcos 1 , g(x) x при x 0.

x

2.15.f (x) 3x4 x5 , g(x) x3 при x 0.

x1

2.16.f (x) 1 x , g(x) 1 x при x 1.

x1

2.17.Порядок малости какой функции выше в точке x = 0: f (x) tgx sin x или g(x) x?

28

2.18. Порядок малости какой функции выше в точке x = 1:

f (x)	ln2	2 x		tg x sin x	или g(x) sin x 1	2	cosx ?
	1 x		2

2.19. Порядок малости какой функции выше в точке x = 0

	f (x)	x3	или g(x) x2 ?
		3 x

Исследовать функции на непрерывность, классифицировать точки разрыва:

			1	, x 0,
2.20.	sin
	f (x)		x
		x 0.
	0,

1 x2, x , 1 ,

2.21. f (x) x , x 1,1 ,

		x		, x 1, .
sin
		2

	ctgx, x 1,
2.22. f (x)	1 x, 0 x 1,
	ln 3 x
						, x 0.
				x 4
2.24. f (x)				x2	tg x 1 .
				x

tgx, x 0,

1, x 0,

2.23. f (x) x, 1 x 0,

ln 1 x2 , x 1.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1.Архипов Г.И., Садовничий В.А., Чубариков В.Н. Лекции по математическому анализу. М.: Высшая школа, 1999.

2.Фихтенгольц Г.М. Основы математического анализа. Т. 1. СПб.:

Лань, 2006.

3.Пискунов Н.С. Дифференциальное и интегральное исчисления. М.: Физматлит, 1985.

4.Корн Г., Корн Т. Справочник по математике. Для научных работников и инженеров. М.: Наука, 1974.

29

Глава 3. ПРОИЗВОДНЫЕ ФУНКЦИЙ ОДНОЙ

ИНЕСКОЛЬКИХ ПЕРЕМЕННЫХ

3.1.Определения, основные теоремы и формулы

Определение 3.1. Производной функции y = f(x) по аргументу x

называется предел lim	f (x +	x) − f (x)	, если он существует.
		x
x→0

dy

Обозначается производная от функции y = f(x) либо dx , либо

f ′(x) . Первая производная может рассматриваться как функция, и

поэтому от нее можно также брать производную и так далее. Таким

d 2 y

образом, мы приходим к понятию второй производной dx2 , треть-

ей и т.д.

Определение 3.2. Первым дифференциалом функции y = f(x) в точке x0 называется линейная часть приращения функции в точке x0 и обозначается dy = f ′(x0 ) dx .

Дифференциал можно использовать для приближенного вычисления функции в точке х0 + х, если функция и ее производная f (x0 + x) = f (x0 )+ f ′(x0 ) x известны в точке х0.

В свою очередь, от первого дифференциала можно взять свой первый дифференциал. При этом символ dx ≡ x трактуется как постоянная величина (понятно, что только для операции дифференцирования!) и называется вторым дифференциалом d 2 y = f ′′(x0 ) dx2 .

Как видим, взятие дифференциала есть просто взятие производных соответствующих порядков от исходной функции.

Правила взятия производной от элементарной функции:

1)

(Cu)′ = Cu′,

′

′

′

4)

u

=

u v −uv

,

2)

′

= u

′

+ v

′

,

v

2

(u + v)

v

3)

(uv) = u v + uv

,

5)

df (ϕ(х))

= df dϕ .

′

′

′

dx

dϕ

dx

30