Башуров Методика решения математических задач 2011

y

	I		I	I
	– 1	0	1	2		x
				Рис. 3.3
	3. Для построения «хвостов» удобно оставить в числителе и
	знаменателе наиболее быстро растущие слагаемые				x2	= x , а это –
					x

очень простая функция (рис. 3.4).
y	"хвост"

I		I		I
– 1	0	1	2	x

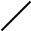"хвост"

Рис. 3.4

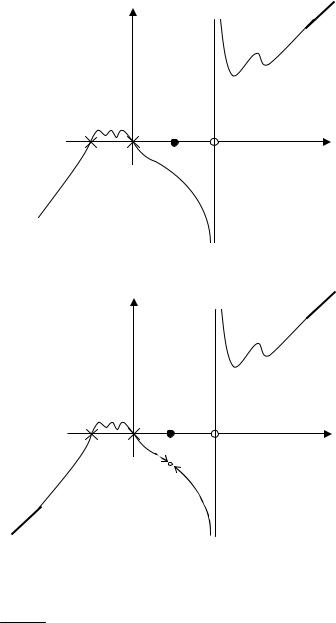
4. А теперь строим график (рис. 3.5) и выкалываем точку на графике, отвечающую x = 1 (рис. 3.6).

41

"хвост"

y

I		I		I
– 1	0	1	2	x

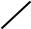"хвост"

Рис. 3.5

"хвост"

y

I		I		I
– 1	0	1	2	x

"хвост"

Рис. 3.6

5. Для построения графика с точки зрения «исследования функции» на рис. 3.4 добавим точки, отвечающие корням уравнения

x(x +1) ′ = 0 :x −2

42

	(2x +1)(x −2) − x			2 −2				2
						= 0	,	x – 5x –2 = 0,
		x −2
x = 5 + 25 +8			= 5 + 33				,	x	2	= 5 − 33 .
1		2		2						2

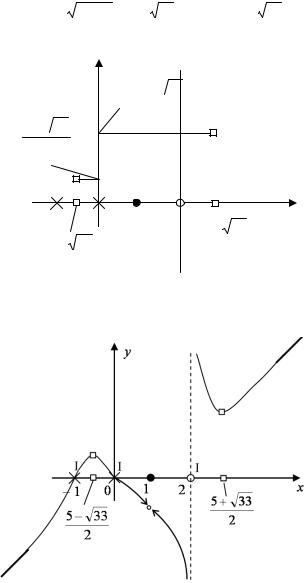
6. Вычисляем значения функции в этих точках (рис. 3.7). y

f 5 + 332

f 5 − 332

I		I		I
– 1	0	1	2	x
5 −	33			5 + 33
				2
	2
		Рис. 3.7

7. Соединяем все точки монотонной кривой и выкалываем точ-

ку x = 1 (рис. 3.8).

Рис. 3.8

43

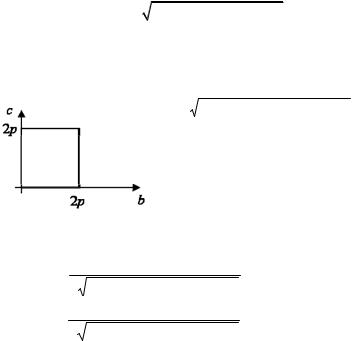
Пример 3.5. Требуется найти треугольник с заданным периметром 2p, имеющий наибольшую площадь.

Из всех известных формул для определения площади выберем формулу Герона S = p( p − a)( p −b)( p − c) , где a, b, c – длины

сторон, 2p = a+b+c. Здесь S выступает в роли функции, а в качестве аргументов – длины сторон a, b, c.

Поскольку сумма сторон равна 2p, то можно уменьшить число аргументов, выразив a через стороны b и c. В этом случае функция

S = p(b + c − p)( p −b)( p − c)

является

функцией двух аргументов b и c, а областью, в которой должен искаться макси-

мум, является прямоугольник, изображенный на рис. 3.9.

Найдем частные производные функ-

Рис. 3.9 ции S по переменным b и c и приравняем их нулю:

1

Sb′ = 2 p(b + c − p)( p −b)( p −c) p( p −c)(2 p − 2b −c) = 0 ,

1

Sc′ = 2 p(b + c − p)( p −b)( p −c) p( p −c)(2 p − 2c −b) = 0 .

Решение этой системы дает стационарные точки. В данном слу-

	чае это одна точка с координатами (b, c), где	b =	2	p, c =	2	p .
			3		3

Отсюда сразу следует, что и третья сторона также равна трети

периметра.

Замечание. То, что найденная точка является стационарной, следует из определения. Но для того, чтобы убедиться в том, что она является экстремальной и к тому же дает максимум функции S, требуется проверить выполнение достаточных условий максимума. Однако в рассматриваемой задаче здравый смысл позволяет избежать процедуры вычисления вторых производных функции S – найденная точка не может быть никакой другой, кроме как точкой максимума.

44

Пример 3.6. Найти, если существует, производную неявной функции, задаваемую уравнением xy − y2 = 0 в точке x=1, y=1.

«Справочным бюро» для задач настоящей главы является п. 3.1. Сначала мы должны установить, какая из переменных (x или y) является функцией, а какая – аргументом. С этой целью найдем част-

ные производные функции f (x, y) = xy − y2 и выясним, в каких точках отлична от нуля производная по x – в этих точках функцией может служить переменная x, и в каких – производная по y – в этих точках роль функции может выполнять переменная y. В точках, в которых одновременно обе производные отличны от нуля, выбор переменной в качестве функции произволен.

Выбрав в качестве функции переменную y и используя форму-

лу (3.1), получим ответ

dy

= −

fx′

=

y

=

1

. A выбрав в качестве

dx

2 y

fy′

2

функции переменную x,

получим

dx

= −

f y′

= 2 .

dy

fx′

Замечание 1. Понятно, что другая переменная играет роль ар-

гумента неявной функции.

Замечание 2. Если в задаче указана точка M (x0, y0), в которой требуется найти производную неявной функции, определяемой уравнением f (x, y) = 0 , то сначала необходимо проверить, удовле-

творяют ли координаты точки M уравнению f (x0 , y0 ) = 0 .

Если не удовлетворяют, то задача теряет смысл.

x2 − y2 + z2 −u2 = 0,	Требуется ука-
Пример 3.7. Дана система
xz = 0.

зать, какие из переменных являются неявными функциями, а какие

– аргументами этих функций в точках: (0, 0, 0, 1); (1, 1, 0, 0); (0, 0, 0, 0).

Рассмотрим первую точку. Проверим, удовлетворяют ли ее координаты исходной системе. При подстановке получаем −1 ≠ 0 , следовательно, задача не имеет смысла в данной точке. Вторая и третья точки проверку, как легко убедиться, проходят, и поэтому приступаем к решению вопроса о выборе функций.

45

Рассмотрим сначала точку (1, 1, 0, 0). Составим матрицу из первых частных производных всех функций, входящих в систему

2x − 2 y 2z − 2u			. Подставим вместо общих выражений для про-
	0 x 0
z

изводных их значения в указанной в условии точке. Полученные

	2		− 2 0	0
числа образуют числовую матрицу						. Минор, образо-
		0	0 1	0

ванный первым и вторым столбцами, имеет ненулевой определитель, и поэтому в качестве неявных функций могут быть в точке (1,

1, 0, 0) выбраны переменные y и z, а в качестве их аргументов – переменные x, u.

Проделывая подобную процедуру в третьей точке (0, 0, 0, 0), видим, что в функциональном определителе (3.2) первая и вторая строки состоят из одних нулей, определители всех миноров второго порядка равны нулю, и поэтому нельзя выбрать в качестве неявных функций ни одну пару переменных. В этом случае требуется проведение дополнительных исследований, но в нашем курсе такие процедуры не предназначены к изучению.

3.3. Задачи для самостоятельного решения

Найти производные следующих функций:

3.1.у = хх.

3.2.	1
	y = (ln x)x .
3.3.	ln x
	y =(x) x .
3.4.	y = (sin x)cos x .
	3x2		−5x			+ 2	, x ≠1, в точке x = 1, x = 3.
3.5.	f (x)=
			x −1
	1,		x =1,
	x2 sin			1	, x ≠ 0,
3.6.
	f (x) =			x			в точке x = 1, x = 0.

0, x = 0,

46

3

2

2

3.7.

tg

x

+ x

sin

, x ≠ 0,

в точке x = 1, x = 0.

x

f (x) =

0,

0, x =

ln

1 + x2

sin x

2

, x ≠ 0,

(

)

3.8.

f (x) =

x

в точке x = 1, x = 0.

x =

0,

0,

xx −1

, x ≠1,

3.9.

f (x)=

в точке x = 2, x = 1.

x −1

1,

x =1,

sin (x

−1)

, x

≠1,

3.10.

f (x)= 3(x2 −1)

в точке x = 1.

1

2 , x =1,

3.11.f (x)= 3 x x в точке x = 3, x = 0.

Исследовать функции и построить график с точки зрения задач на исследование функции:

		3	2	2	x > 0,
3.12.	3		x	− x ,
	y =			x ≤ 0,
	xex ,

3.13.y = x2 − x −1 .

x−8

x3 − 2 x

3.14. y = (x −1)x .

3.15.

y =

x2 −3

x

+1

.

x +1

3.16.

y =

x2

− 7x + 6

x2 − 4

.

x −1

x

+ 2

3.17.y = ln(x +1).

x2 − 4

47

Построить полином Тейлора без остаточного члена для функции в окрестности точки x0, содержащий, по крайней мере, не меньше четырех слагаемых:

		x	+5
	3.18. f (x) = e 3			, x0	= 0.

3.19.f (x) = (x + 2)e2 x , x0 = 0.

3.20.	f (x) = cos x3 ,					x0 = 0.
3.21.	f (x) =sin2 x ,					x0 = 0.
3.22.	f (x) =sin x2 ,					x0 = 0.
3.23.	f (x) =		x2 −1		,	x0 = –2.
3.24.	f (x) =		x ln(1+ x2 ), x0 = 0.

Построить полином Тейлора без остаточного члена для функции в окрестности точки (x0, y0):

3.25.f (x, y) = x2 + 2xy −3y2 +11x −5y +9 , x0 = –2, y0 = 2.

3.26.f (x, y) = ex sin y , x0 = 0, y0 = 0 до членов третьего поряд-

ка включительно.

3.27.f (x, y) = yx , x0 = 0, y0 = 0 до членов второго порядка включительно.

3.28.f (x, y) = exy , x0 = 0, y0 = 0 до членов третьего порядка

включительно.

3.29.f (x, y) = ex+y , x0 = 0, y0 = 0 до членов третьего порядка включительно.

3.30.f (x, y) = ex2 −y , x0 = 2, y0 = 1 до членов второго порядка

включительно.

3.31.f (x, y) = sin(x2 y) , x0 = 0, y0 = 1 до членов третьего по-

рядка включительно.

Решить задачи:

3.32. Из всех прямоугольных треугольников с данной гипотенузой a найти треугольник наибольшего периметра.

48

3.33.Какой из прямоугольных треугольников с заданным периметром 2p имеет наибольшую площадь.

3.34.Данное положительное число a разложить на два слагаемых так, чтобы их произведение было наибольшим.

3.35.Кусок проволоки данной длины l согнуть в виде прямоугольника так, чтобы площадь последнего была наибольшей.

3.36.Из всех треугольников данного периметра 2p, найти тот, который имеет наибольшую площадь.

3.37.Есть три положительных числа. Найти максимальную сумму их квадратов, если сумма чисел не превосходит 10.

3.38.Найти параллелепипед, имеющий при заданном объеме V, наименьшую поверхность.

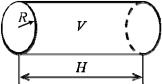
3.39.Попытайтесь спроектировать

железнодорожную цистерну для Рос-
сийских железных дорог, имеющую
форму кругового цилиндра (рис. 3.10)
вместимостью 60 кубических метров и
такую, чтобы: 1) общая площадь по-	Рис. 3.10
верхности цилиндра была минимально
возможной; 2) длина сварного шва
была минимальной длины.

3.40.Дан конус высотой H и радиусом основания R. Требуется вписать прямой параллелепипед максимального объема.

3.41.Найти круговой конус максимального объема, если боковая поверхность равна S.

3.42.Существует ли неявная функция, определяемая уравне-

нием x2 − y2 + xy + y3 − x = 0 , в точках (0,0), (1,1)?

3.43.Существует ли неявная функция, определяемая уравне-

нием x2 − y2 + 3xy = 3 , в точках (1,2), (1,1)?

3.44.Существует ли производная неявной функции, определяемой уравнением x4 −3x2 y + y3 + (y −1)2 − x = 0 , в точках (0,0),

(1,1)?

3.45. Существует ли производная неявной функции, определяемой уравнением (y − 2)2 exy −sin x = 0 , в точке (1,2)?

49

3.46.Найти производную неявной функции y = y(x), определяемой уравнением cos(πx2 y) + xy + 2y2 = 0 .

3.47.Найти частные производные неявной функции z = z(x,y),

z

определяемой уравнением z2 − tg (xyz)+ e xy −1 = 0 , в точке (1, 1, 0). 3.48. Найти частные производные по x неявной функции z = z(x,y), определяемой уравнением 2x2 + 2 y2 + z2 −8xz − z +8 = 0 ,

вточке (2,0,1).

3.49.Существует(ют) ли неявная(ые) функция(и), определяе-

2

2

2

мая(ые)

системой x

+ xy + z

+t

− 4t = 0,

в точках (0,0,0,0),

xz

− y2 + z2 −t = 0,

(1,1,1,1)? Найти производные.

3.50.

Найти

производные

неявных функций, определяемых

2

+ x − z =1,

в точках (0,1,0), (1,1,1).

системой y

x2

− y2

+ xz − yz2 = 0,

3.51.

Найти

производные

неявных функций, определяемых

2

+sin (xy)+ z = 2,

системой

x

в точках (1,π,0), (1,0,1).

+ x − z = 0,

y2

3.52.

Найти

производные

неявных функций, определяемых

системой x + y − z + t = 2,

в точках (1,0,0,–1), (1,1,1,1).

2x + 2 y −3z −t = 0,

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1.Архипов Г.И., Садовничий В.А., Чубариков В.Н. Лекции по математическому анализу. М.: Высшая школа, 1999.

2.Фихтенгольц Г.М. Основы математического анализа. Т. 1. СПб.:

Лань, 2006.

3.Пискунов Н.С. Дифференциальное и интегральное исчисления. Т.1. М.: Физматлит, 1985.

4.Корн Г., Корн Т. Справочник по математике. Для научных работников и инженеров. М.: Наука, 1974.

50