Башуров Методика решения математических задач 2011

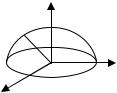
2 1

∫∫xsin(xy) dx dy = ∫dy∫x sin (xy) dx , то нам предстоит достаточно

D

1 0

1

долгая процедура взятия интеграла∫x sin xy dx . Поэтому восполь-

0

зуемся возможностью поменять порядок повторного интегрирования и представим двойной интеграл в виде

1 2

∫∫xsin(xy) dx dy = ∫dx∫x sin (xy) dy .

D

0 1

Этап 4 решения задачи заключается во взятии двух «табличных» интегралов:

		1								1
∫∫xsin(xy) dx dy = −∫cos (xy)									12 dx = ∫(cos x −cos 2x) dx =
D		0								0
		1						1			1		sin 2 .
= sin x −				sin 2x						= sin1 −
		2									2
								0
Пример 5.2. Взять	тройной				интеграл						∫∫∫(x2 + y2 + z2 )dv , где
											V

область V – верхняя полусфера радиуса 3 с центром в начале координат (рис. 5.5)

Поскольку область интегрирования от-				z
носится к третьему типу (см. рис. 5.4),
применим для нахождения интеграла стан-				3
дартный способ, а именно перейдем к сфе-
рическим	координатам:	x = rsinθcosφ,	x	y
y = rsinθsinφ, z = rcosθ.				Рис. 5.5

Сделаем замену переменных в подынтеграль-

ной функции

x2 + y2 + z2 = (r sinθcosφ)2 + (r sinθsinφ)2 + (rcosθ)2 = r2,

а также не забудем о якобиане J = r2sinθ.

Формула для вычисления интеграла принимает вид:

		π
	3	2	2π	5
∫∫∫(x2 + y2 + z2 )dv = ∫dr∫dθ∫r4 sin θ dϕ = 2π				3 .
V	0	0	0	5

71

5.3. Задачи для самостоятельного решения

Найти интегралы:

2

2

25

4

4

5.1.

6x

y

+

x

y

dxdy , D – область,

определяемая

сис-

∫∫D

3

темой x = 1,

y = x2, y = − x .

∫∫6 ye

xy

5.2.

3

dxdy ,

где D – область, определяемая системой:

D

x = 3, x = 6, y = ln2, y = ln3.

5.3.

∫∫y sin xydxdy , где D – область,

определяемая системой:

D

x = 1, x = 2, y

=

π

, y = π.

2

5.4.

∫∫∫2 y2 zexyz dxdydz , где V – область,

определяемая

систе-

V

мой: x = 0, x = 1, y = 0, y = 1, z = 0, z = 1.

5.5.

∫∫∫(15x + 30z)dxdydz , где V– область,

определяемая

сис-

V

темой: x = 1, y = 0, y = x, z = 0, z = x2 + 3y2.

5.6.

∫∫∫(1 + 2x3 )dxdydz , где V– область,

определяемая

систе-

V

мой: x = 1, y = 0, y = 9x, z = 0,

z =

xy .

5.7.

∫∫∫x2 z sin xyz dxdydz , где V–

область,

определяемая

сис-

V

темой: x = 0,

x = 2, y = 0, y = π, z = 0, z = 1.

Найти площадь фигуры, ограниченной данными линиями:

	5.8.	y =		6 − x2 , y =		6 − 6 − x2 .
	5.9.	y =	3	x , y =	3	, x = 9.
					2x
		2				z = ex .
	5.10. x = 0, z = 0, x = 2,						x
	5.11. y2 − 2x + x2 = 0 ,					y2 − 4x + x2 = 0 , y =		, y = 3x .
							3

72

5.12.y2 − 4 y + x2 = 0 , y2 −8 y + x2 = 0 , y = x, x = 0.

5.13.y = 3x , y = 8ex , y = 3, y = 8.

Пластина D задана ограничивающими кривыми, ρ – поверхностная плотность. Найти массу:

5.14.D: x = 1, y = 0, y2 = 4x, y ≥ 0; ρ = 6x +3y2.

5.15.D: y2 = 10x + 25, y2 = –6x + 9; ρ = 2y2.

5.16.D: x2 + y2 =1 , x2 + y2 = 9 , x ≥ 0, y ≥ 0;

ρ =

x + y

.

x2 + y2

x2

y2

4

5.17. D:

+

≤1;

ρ = x .

4

25

x2

y2

3

5.18. D:

+

≤1, x ≥ 0, y ≥ 0; ρ = x y.

4

9

Найти объем тела, ограниченного поверхностями:

5.19. y =

15x , y =

15x , z=0, z =

15(1+ x) .

5.20. y = −3x2 + 5 , y = 2, z = −1+

5x2 + y2 ,

z = 3 + 5x2 + y2 .

5.21. z =

4

− x2 − y2

, z = x2 + y2 .

9

5.22.z = 4 −6(x2 + y2 ), z = 12y + 4.

5.23.y2 + x2 = 4x , z = 10 – y2, z = 0.

5.24.z = 16 − x2 − y2 , 6z = x2 + y2 .

5.25.x2 + y2 + z2 =1 , x2 + y2 + z2 =16 .

5.26.x2 + y2 + z2 ≤ 2x

Тело V задано ограничивающими его поверхностями,

ρ– плотность. Найти массу:

5.27.x = 0, x = 3, y = 0, y = 4, z = 0, z = 2; ρ = x + y + z .

5.28.z =1 − x2 − y2 , z = 0; ρ=5z .

5.29. x2 + y2 + z2 =1, x2 + y2 = z2 , x = 0, y = 0, x ≥ 0, y ≥ 0, z ≥ 0; ρ = 32z .

73

5.30. x2 + y2 + z2 = 4 , x2 + y2 = z2 , x = 0, y = 0, x ≥ 0, y ≥ 0, z ≥ 0;

ρ= 6z .

5.31.x2 + y2 = 1649 z2 , x2 + y2 = 74 z , x = 0, y = 0, x ≥ 0, y ≥ 0, z ≥ 0;

ρ=80 yz .

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1.Архипов Г.И., Садовничий В.А., Чубариков В.Н. Лекции по математическому анализу. М.: Высшая школа, 1999.

2.Фихтенгольц Г.М. Основы математического анализа. Т. 2. СПб.:

Лань, 2006.

3.Пискунов Н.С. Дифференциальное и интегральное исчисления. Т.2. М.: Физматлит, 1972.

74

Глава 6. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

6.1. Определения, основные теоремы и формулы

Для существования определенного интеграла необходимо выполнение двух условий: ограниченности промежутка [a,b] (для того чтобы была возможность разбить его на конечное число отрезков, длины которых не превышают некоторого числа ) и ограниченности функции f(x). При нарушении какого-либо условия или обоих сразу появляется необходимость в двух несобственных интегра-

лах.

Определение 6.1. Пусть функция f(x) определена на промежут-

Ak

ке [a, ∞). Рассмотрим последовательность ∫ f (x)dx для Аk, стре-

a

мящихся к бесконечности. Если эта последовательность имеет предел, то он называется несобственным интегралом первого рода и

∞

обозначается ∫ f (x)dx .

a

Схожим образом определяется несобственный интеграл и в случае промежутка (−∞, a] и промежутка (−∞,+∞). Сходимость

(т.е. существование) интеграла обосновывается тремя теоремами: Теорема 6.1 (признак Коши). Если функция f(x) неотрицатель-

ϕ(x)

на, представима в виде f (x)= xα , то:

1)если α > 1 и функция φ(x) ограничена, то интеграл существует (или сходится);

2)если α ≤ 1 и функция φ(x) отделена от нуля, т.е. ϕ(x)≥ ε >0,

то интеграл не существует (или расходится).

Теорема 6.2 (признак Дирихле). Пусть имеем две функции f(x) и g(x), определенные и непрерывные на промежутке [a, ∞), g(x) –

∞

монотонна. Для сходимости интеграла ∫ f (x)g (x)dx достаточно,

a

чтобы:

75

A

1) функция Φ(А)= ∫ f (x)dx была ограниченной функцией от

a

А: Φ(А) ≤ C (C = const, a ≤ A < ∞) (хотя предела limΦ(А) может

A→∞

ине существовать);

2)g(x)→ 0 при x → ∞ .

∞

Теорема 6.3. Если интеграл ∫ f (x) dx существует, то сущест-

a

∞

вует и интеграл ∫ f (x)dx .

a

Определение 6.2. Пусть функция f(x) определена на промежутке [0,b] и при x → 0 стремится к бесконечности. Рассмотрим по-

следовательность {εk }, стремящуюся к нулю при k → ∞ , и соот-

b

ветствующую последовательность интегралов ∫ f (x)dx . Если по-

εk

следняя последовательность имеет предел, то он носит название несобственного интеграла второго рода и имеет обозначение

b

∫ f (x)dx .

0

Замечание. Если несобственный интеграл первого рода имеет характерную отметку ∞, то интеграл второго рода ничем внешне не отличается от обыкновенного интеграла. Чтобы установить, имеем ли мы дело с несобственным интегралом, требуется заглянуть «внутрь» его.

Для установления сходимости интеграла второго рода исполь-

зуется признак Коши.

Теорема 6.4 (признак Коши). Если функция определена на

	промежутке [0, b] и подынтегральная функция имеет вид	ϕ(x)	, то:
		xα

1)при α < 1 и функция φ(x) ограничена, и интеграл существует;

2)при α ≥ 1 и функция φ(x) в окрестности точки 0 отделена от

нуля (т.е. ϕ(x) ≥ ε > 0 ), и интеграл не существует.

76

В общем случае необходимо анализировать все точки, в которых подынтегральная функция не ограничена, и каждую такую точку рассматривать отдельно.

Полезной как для интеграла первого рода, так и второго является теорема сравнения.

Теорема 6.5. Если подынтегральная функция положительна, то имеет место следующее утверждение: если f (x) ≥ ϕ(x) , то из схо-

b

димости интеграла ∫ f (x)dx следует сходимость интеграла

a

b

b

∫ϕ(x)dx , а из расходимости интеграла ∫ϕ(x)dx следует расходи-

a

a

b

мость интеграла ∫ f (x)dx . Здесь а и b могут быть «равны» беско-

a

нечности.

Фигурирующие в теореме сравнения функции ϕ(x) и f (x) называются, соответственно, минорантой и мажорантой.

6.2. Примеры решения задач

∞ sin 2x			dx .
Пример 6.1. Исследовать сходимость интеграла ∫	x	2
1

Признак Дирихле сразу дает ответ – интеграл сходится, так как

		1				Φ(А)		A
	g(x) =		→0	при	x → ∞ и		=	∫sin 2x dx	≤1.
		2
		x						1

Не вздумайте применить признак Коши – подынтегральная функция не является положительной (или отрицательной)!

∞		sin x
Пример 6.2. Исследовать сходимость интеграла ∫				dx .
		x
1

Поскольку интеграл является интегралом от положительной функции, переберем все указанные в п. 6.1 способы исследования сходимости несобственных интегралов первого рода. Признак Ко-

77

5 dx .

ши не решает вопроса, так как функция sin x , стоящая в числителе

подынтегрального выражения, не «отделена» от нуля. Попытаемся найти миноранту (тем самым мы подозреваем, что

интеграл расходится)

sin x

≥

sin2 x

.

x

x

∞

x

1

∞

1 −cos 2x

Полученный интеграл

∫

sin2

dx =

∫

dx

можно раз-

2

1

x

1

x

бить на два интеграла 1

∞

1 dx

и 1

∞

∫

∫cos 2x dx . Первый интеграл

2

1

x

2

1

x

расходится, так как выполнены все условия применимости признака Коши: α = 1, ϕ(x) =1 отделена от нуля. Второй интеграл сходит-

ся (по признаку Дирихле).

Разность расходящегося и сходящегося интегралов дает расходящийся интеграл. Тем самым, мы установили, что интеграл от ми-

∞

sin x

норанты расходится и, следовательно,

интеграл

∫

dx также

x

1

расходится.

6.3. Задачи для самостоятельного решения

Исследовать сходимость интегралов:

∞

x2 +3

∞

e−x

6.1. ∫

dx .

6.5. ∫

dx .

x

3

xe

−x

+10x

+1

0

+3x + 4

1

∞

x

∞

2 −sin x2

6.2. ∫

dx .

6.6. ∫

dx .

x

3

+ x

2

+ x

+1

3

1

1

0 x2

+ x2 +1

∞ sin2 3x

6.3.∫0 3 x4 + 2 dx .

∞

6.4. ∫x2e−x dx .

0

+∞ e−(x2 −1)

6.7. ∫

−∞1+3 x 4

∞

6.8. ∫sin x2dx .

0

78

−∞∫ x2 +5x +11 dx .

∞ ln (41− x)dx .

cos2 x

0

0

6.11. ∫

x4

∞

6.9. ∫cos x3dx .

0

∞ sin x2						1
6.10. ∫								dx .
		3		2		+ x
0	x2

6.12.

	∞
6.13.	∫cos x sin x dx .
	0				x						x
	∞
6.14.	∫	cos x						dx .
		6
	5		x		5
	1			1
6.15.	∫										dx .
	−1		1− x
	1				x
6.16.	∫											dx .
			1− x							2
	0
	0						x	3
6.17.	∫													dx .
			16 − x										4
	−2
	2		x	2			−		3x
6.18.	∫													dx .
	0 sin x											x

1 x2 + x			dx .
6.19. ∫
0 sin 2x		x

6.20. 1∫ x2 ln(x3 + x)dx .

0

	1
6.21.	∫ x3 ln x3dx .
	0
	1								x		3				− x				2
6.22.	∫																						dx .
			3														π
	0		x2 cos																− x
																	2
	1		ln (1+ x)
6.23.	∫																	dx .
										5
	0							x2
	1	tg x
6.24.	∫								dx .
		3
	0		x		2
	1				tg x
6.25.	∫																dx .
			5												3
	0		x	2		+ x									2
	1		ln (x2 − x)
6.26.	∫																				dx .
												1
	0								x2

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1.Архипов Г.И., Садовничий В.А., Чубариков В.Н. Лекции по математическому анализу. М.: Высшая школа, 1999.

2.Фихтенгольц Г.М. Основы математического анализа. Т. 2. СПб.:

Лань, 2006.

3.Пискунов Н.С. Дифференциальное и интегральное исчисления. Т.2. М.: Физматлит, 1972.

79

Глава 7. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ

7.1. Определения, основные теоремы и формулы

Пусть нам задана некоторая кривая Г, заданная векторным уравнением r = r (t), или в координатной форме этого уравнения

x =ϕ(t), y = ψ(t), z = χ(t).

Значение параметра t = t0 задает начальную точку кривой, а значение параметра t = t1 – конечную точку М1. Пусть в точках М кривой Г задана функция f(М).

Введем разбиение { sk } кривой Г на криволинейные «отрезки» sk . Выберем на каждом криволинейном «отрезке» sk точку Мk и

N

составим сумму Римана ∑ f (Mk ) sk .

k =1

Определение 7.1. Если предел интегральной суммы Римана

N

∑ f (Mk ) sk при длинах «отрезков» sk , стремящихся к нулю,

k =1

существует и не зависит ни от способа разбиения, ни от выбора точек {M k }, то он называется «криволинейным интегралом перво-

го рода от функции f(М) по кривой Г и обозначается ∫ f (М)ds .

Г

Если ясно, о каком интеграле идет речь, употребляют термин «криволинейный интеграл». Если неясно, то приходится пользо-

ваться полным названием «криволинейный интеграл первого рода по кривой Г от функции f(M)».

Криволинейный интеграл обозначается как ∫ f (M )ds или

M0M1

∫ f (x, y, z)ds . Его свойства те же, что и у определенного интегра-

Г

ла. Специально отметим три:

1) ∫ ds = L(Г), где L(Г)– длина кривой Г.

Г

80