Башуров Методика решения математических задач 2011

Часто оказывается полезной формула Стирлинга, позволяющая заменять факториал при больших n другим аналитическим выражением n! 2 n e n nn .

1.2. Примеры решения задач

Пример 1.1. Найти предел последовательности

lim	3n2 n	32 n	12	.
	7	5n2
n	18n 2

Впоисках ответа будем тщательно придерживаться предложенной нами в предисловии схемы решения.

На этапе 1 классифицируем задачу как относящуюся к области математики «исследование последовательностей». Из этого следует, что выполнение этапа 2 заключается в том, что мы должны вспомнить ряд теорем и формул из п. 1.1 (нашего «справочного бюро») и основной принцип нахождения пределов – сведение заданной последовательности к эталонной. На этапе 3 мысленно строим схему решения.

Вданном примере естественно пытаться применить формулу, устанавливающую, что предел дроби есть частное от пределов числителя и знаменателя. Однако эта формула не применима, поскольку нет ни того, ни другого предела (имеем дело с

неопределенностью вида ) . Попытаемся вынести из знаменателя

и числителя множитель п и на вынесенный множитель сократить и числитель и знаменатель:

3n

1

3n2

3

n

n

n 2

n

.

lim

= lim

7

5n2

5

n 18n 2

n

18n 2 5n

К сожалению, прием не привел к успеху – все осталось по-

прежнему (неопределенность вида ). Попытаемся вынести

7

множитель n2 , и сократить на него вновь и числитель и знаменатель:

11

	3n2 n32			3					1				1
			n
lim				= lim	n	3	2		n	2			n	3		.
	7	5n2									5
n 18n 2				n			18
										n32

Теперь каждое слагаемое и в знаменателе и числителе есть, по сути, эталонные последовательности и, стало быть, и сумма также имеет предел, равный сумме пределов эталонных последовательностей. Формула, содержащаяся в теореме 1.1, имеет «право на жизнь», и мы переходим к этапу 4 – этапу реализации наших рассуждений на бумаге:

								3			1				1			lim	3				1				1
		2		32
	3n		n			n															3		n	2			n	3
								3				2				3
lim							= lim	n	2		n				n		=	n	n		2									=
			7	5n2									5												5
n	18n 2						n		18
																		lim			18
													3
																									3
												n 2						n						n 2

3					1				1
	lim		lim						lim
		3					2						3
=	n n 2			n n						n n					=0.
		lim18 lim								5
									3
		n			n n 2

Этап 5 в данном примере заключается, на наш взгляд, только в проверке арифметических действий.

И последнее. Не абсолютизируйте предлагаемый нами подход к поиску способа решения и нахождения ответа на предлагаемую задачу. Если вы на своем пути не допустили ошибок ( например, использовали какие-то формулы, не обосновав законность их применения) – то никто не имеет право упрекнуть Вас в неправильности предлагаемого Вами решения! И еще удобно в самом начале перейти к единому обозначению степени.

Замечание. Нетрудно заметить, что в примерах с

неопределенностью вида , когда числитель и знаменатель

представлены как многочлен целой или дробной степени: 1) предел a = , если в числителе старшая степень при n больше, чем в знаменателе; 2) предел a = 0, если в числителе старшая степень при n меньше, чем в знаменателе; 3) предел a равен отношению коэффициентов при старших степенях, если в числителе и знаменателе старшие степени при n одинаковы.

12

Пример 1.2. Найти предел последовательности

sinn 3cosn

3n5

2 n12

lim

.

1

n3

1

n

n2n 2

Сразу видно,

что перед

нами

произведение

двух

3n

5

2

n

12

последовательностей, предел одной из них

мы уже

1

n3

n2n

2

1

умеем находить. Вторая последовательность

{sinn 3cosn}

из-за

знакомого нам поведения синуса и косинуса предела не имеет, но заключена в промежутке [–4, 4]. Это, в первую очередь, означает, что мы не можем воспользоваться для нахождения предела формулой из теоремы 1.1, но можем попытаться использовать «принцип двух милиционеров» (кстати, в нашем «справочном бюро» больше ничего подходящего отыскать не удается).

Переходим к этапу 4, т.е. берем бумагу и перо и получаем:

4

3n

52 n12

sinn 3cosn

3n

5

2

n12

4

3n52

n12

.

1

1

1

n2n 2 n3 1

n2n 2 n3 1

n2n

2 n3 1

Так как

3

1

3n52 n12

lim 4

= 4 lim

n12

n2

= 0

1

n

n2n

2 n3 1

n

1

1

1

и

n12

n3

5

2 n

1

lim 4

3n

2

= 0 ,

1

n3 1

следовательно,

n

n2n 2

sinn 3cosn

3n

52

n

12

lim

=0.

2

3

n

1

2

n

1

n

n

Этап 5 – проверка – состоит в том, чтобы на всякий случай

убеждиться в правильности использованных формул.

Замечание

1.

А

вот

пример

на

нахождение

предела

последовательности

sinn 3cosn 1

n

n

1

данным

lim

n

n

1

13

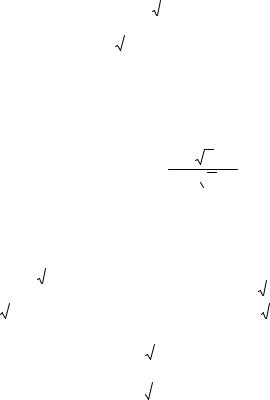
способом решен быть не может. Обе последовательности, составляющие заданную последовательность, пределов не имеют, и поэтому «принцип двух милиционеров» в нашем случае неприменим.

Замечание 2. У тех, кто в свой «справочник» включил другие теоремы из раздела «Числовые последовательности» (например, из учебника [2]), могут решить данные задачи и по-иному – например, задачу 1.1 можно решить, сославшись на теорему о пределе последовательности, являющейся произведением двух других, одна из которых имеет пределом число 0, а вторая – является ограниченной.

Пример 1.3. Найти предел последовательности

1

3n2

n

n 1

1

lim

n2

.

2n 3 n 3

n

Опускаем первых два этапа, сразу переходим к третьему. В

1

3n2

выражении

1

получается неопределенность вида 1

, т.е.

n2

мы имеем дело с замечательным пределом, если ввести

обозначение m = n2 . Второй сомножитель n n 1 также имеет

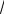2n 3n 3

предел, так как после вынесения за скобку из числителя и знаменателя n предел становится очевиден. Все условия для применения теоремы 1.1 налицо, и мы переходим к этапу 4:

1

3n2

n

n 1

3n2

1

n2

1

n

n 1

=

1

=

lim

lim

lim

2n 3 n 3

n2

3 n 3

n

n

n 2n

1 m 3

1

1

1

1

n

lim

1

lim

n

=

e3 .

3

2

n

m

n

1

2

n

3

n2

14

Этап 5 снова заключается в проверке правильности всех примененных процедур.

Пример 1.4. Требуется найти предел последовательности

lim 32n 1 3n 1 .

n

Вновь теорема 1.1 неприменима, так как и у последовательно-

стей {32n 1} и {3n 1} нет предела (обычно говорят, что предел

равен бесконечности,	т.е. перед нами неопределенность вида
). Попытаемся	преобразовать исходное выражение, т.е.

форму представления общего члена так, чтобы применение этой теоремы стало возможным. Вид общего члена подсказывает, что можно попытаться воспользоваться формулой «разность кубов».

Для

этого

домножим

числитель

и знаменатель на

3

2

3

3

3

2

2n 1

2n 1

n 1

n 1

(мысленно!) и, проделав в

уме несложные арифметические действия, получим, что в

числителе

остается

n 2,

а в

знаменателе выражение

3

2

3

3

3

2

2n 1

2n 1

n 1

n 1

. Этот вид задач нам уже

неоднократно встречался, и этап 4 решения этого примера мы благополучно завершим на бумаге:

										lim 3														3													=
																		2n 1												n 1
										n
3					3											3							2							3												3											3			2
		2n 1																																2n 1
							n 1											2n 1																											n 1										n 1
lim
					3										2 3														3										3											2
n									2n 1											2n 1														n 1										n 1
		= lim																				n 2																																=
		n 3							2n 1						2 3					2n 1								3				n 1						3					n 1						2
																		n13								2
																										2
		= lim																							n 3																												= .
													2																																			2
		n								1											1													1												1
				3 2												2						3				1										3				1
										n											n													n												n
																					15

Этап 5 – проверка законности примененных формул. Следующий пример состоит не в нахождении предела, а в

установлении факта его существованиия.

Пример 1.5. Пусть последовательность задана формулой

n	1
an =			. Требуется доказать, что данная последовательность
k=12k		1

имеет (или не имеет) предел.

Начинаем решение прямо с третьего этапа. Из всех теорем, приведенных в нашем справочнике, только две годятся для решения нашей задачи – «принцип двух милиционеров» и теорема 1.4. Выберем последнюю и попытаемся выяснить, выполнены ли все условия для ее применения.

Так как каждое слагаемое в общем члене положительно, а каждый следующий член an 1 есть предыдущий ап с одним

	лишним слагаемым	1			,	то монотонное возрастание очевидно.
		2n 1	1
	Ограниченность следует из простого неравенства
			n			1		n	1
								<		,
					2	k			k
			k=1			1		k=1	2

и стоящая в правой части сумма есть хорошо известная сумма

убывающей геометрической прогрессии со знаменателем q =			1	,
2
S =	1/2	=1.
1 1/2

Оба необходимых условия выполнены и, поэтому, данная нам для решения задача имеет предел.

Этап 4 – по сути, это выстраивание в одну строчку всех наших рассуждений и «выбрасывание лишних слов». Идеально было бы избежать всех слов, а оставить только цепочку алгебраических выражений, но это тот идеал, который достичь никогда не удается.

Этап 5 вновь заключается в проверке арифметических действий.

16

1.3. Задачи для самостоятельного решения

Найти пределы последовательностей:

		11n5 n52 n14
1.1.	lim																	.
						9		2 n2						3
	n	8n
		2n				2		n					1	e	n
													2
1.2.	lim																		.
													5				1
	n e 3n 2n 2 n																4
					3					9n2
1.3.	lim						n									.
	n 3n							4 9n8 1
		4																					5
1.4.	lim			6n2 n 5n4 1																				n5 6n3 1		.
														n 3
	n																			n 15
					sinn2
1.5.	lim			n										.
										n 1
	n n

1.6.lim 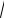42 n4 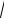2n2 3 . n n sinn n2 1

					2n3 lnn
1.7.	lim ln			4 3n			3						n				.
	n
	lim sin5n cos2n																	5n32					n13					7
1.8.																													.
																			n3 n						1
	n																								2		4
1.9.	lim sinn2 1 n																			n 3						.
	n																n2							n
					n2						1
1.10.	lim n				n 1					n	3								.
	n											1
						n!														n3
																										n
1.11.	lim																											.
																					n 2
	n			n 1 ! n!

1.12.lim 2n 1 ! 2n 2 ! sinn . n 2n 3 ! 2n 2 !

17

1.13.lim 1 3 5 ... 2n 1 .

	n														9n4 1
		1									2											3								2n 1
1.14.	lim																									...									.
											n3											n3									n3
	n n3
									4										8							2n
1.15.	lim				3									3														3
																						3...							.
	n
		5n 1 3n 1
1.16.	lim																			.
				5n				3n
	n
				n 1										n2
1.17.	lim													.
	n 2n 1
								3								n3 n
1.18.																			3					.
	lim 1
								n2
	n
								6								2n n3
1.19.																		n 5
	lim 1
								n3
	n
								4 n											n56					n23
																															n
1.20.	lim 1																																.
																									n		2
	n							n																			3	1

1.21.lim n2 3n 2 n 1 .

n

1.22.	lim	n			1 n		2					n				1 n		2	.
				2		2									2		2
	n
	3
			2						3
1.23.		n			3n 2						n 1
	lim													.
	n

Установить, имеют ли предел последовательности:

n1

1.24.an = k=1 k2 .

n1

1.25.an = k=1 k2 6k 9 .

18

n1

1.26.an = k=1 3k2 5 .

n1

1.27.an = k=1 3k 2 .

1.28. an	=	2n	.
		n!			8				11									8				11				3n 5
1.29. a = 8,a				=									,...,a		n	=								...				,...
																										6n 5
1			2	1				7								1				7
1.30. a = 2,a				=		2				3		,...,a		n		=	2				3		...		n 1		,...
1			2	1				3								1				3					2n 1

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1.Башуров В.В., Огибин В.Н. Условия сходимости итерационных процессов на действительной оси. // Журнал вычислительной математики

иматематической физики. Т. 6. М.: Изд-во АН СССР, 1966. С. 913–916.

2.Фихтенгольц Г.М. Основы математического анализа. Т. 1. СПб.:

Лань, 2006.

19

Глава 2. ФУНКЦИИ ОДНОГО ИЛИ МНОГИХ ДЕЙСТВИТЕЛЬНЫХ ПЕРЕМЕННЫХ

2.4. Определения, основные теоремы и формулы

Если в качестве множества, на котором задается функция, принимающая действительные значения, выступает некоторое непрерывное подмножество множества действительных функций, то перед нами – действительная функция одного действительного переменного. В дальнейшем будем использовать термин «функция».

Если в качестве множества, на котором задается функция, принимающая действительные значения, выступает непрерывное множество n-мерных векторов (x1,x2,…,xn), то такие функции будем называть «функцией многих переменных» (например, функцией двух переменных f (x,y), трех f (x,y,z) и т.д.).

Далее будем рассматривать только функции одного переменного (переход к функциям нескольких переменных будет обозначен специально).

Пусть функция f(x) определена на некотором множестве X. Определение 2.1. Пределом функции в точке x0 называется

число a, к которому сходится последовательность {f (xk)} значений этой функции на любой последовательности {xk}, xk x0 , сходя-

щейся к x0.

Если этот предел совпадает со значением функции в этой точке, то такая функция называется непрерывной в точке x0.

Существует другое определение предела функции. Определение 2.2. Число a называется пределом функции f(x) в

точке x0, если для любого числа 0 существует число 0 такое, что для всех x X , x x0 , удовлетворяющих неравенству

x x0 , выполняется неравенство f (x) a .

Замечание. Оба определения предела функции эквивалентны. Определение 2.3. Если для любой последовательности {xk}, сходящейся к x0 и удовлетворяющей условию xk < x0 (xk > x0) для всех k, соответствующая последовательность f {xk} сходится к одному и тому же пределу, то этот предел носит название «односто-

20