Гаврилов Основы ядерной електроники ч.1 2010

Функция распределения F(x,t0) процесса X(t), или интегральный закон распределения, определяет вероятность того, что в момент времени t0 случайная величина X(t0) будет меньше некоторого значения x:

F (х, t0 ) P[ X (t0 ) x] .

Плотность распределения вероятностей p(x, t0), или дифферен-

циальный закон распределения, вводится как производная от

F(x, t0 ):

p(х, t0 ) F (x, t0 ) .x

С учетом последнего определения, p(x, t0 )dx – это элемент ве-

роятности, который показывает с точностью до бесконечно малой величины высшего порядка вероятность того, что в момент времени t0 случайная величина X (t0 ) находится в пределах от x до

x+dx:

p x,t0 dx P x X t0 x dx .

Указанные выше распределения представляют собой распределения первого порядка и наиболее часто являются результатом измерений. Вообще же говоря, стохастический процесс оказывается полностью определенным, если известны его функции распределения до порядка n . Однако реально функциями распределения выше второго порядка интересуются сравнительно редко. Функция же распределения второго порядка вводится как вероятность того, что случайный процесс X(t) к моменту времени t1 меньше x1 , а к

моменту t2 (на время позже) меньше x2 :
F x1; x2 , τ P X t1	x1, X t2 t1 τ x2		,
а плотность распределения вероятностей:
	2
p x1; x2 , τ		F x1; x2 , τ .
	x1 x2

Таким образом, введенные распределения характеризуют статистическую связь значений X(t1) и X(t2=t1+ ) случайного процесса

X(t).

11

Аналогичным способом можно описать статистическую зависимость двух разных сигналов (процессов) X(t) и Y(t). В этом случае говорят о функции совместного распределения вероятностей F(x;y, ) и о плотности совместного распределения вероятностей p(x;y, ). Функция распределения, указывающая, с какой вероятностью амплитуда сигнала (значение процесса) X(t) к моменту времени t+ меньше предела x2, если к моменту времени t величина амплитуды составляет x1 и она известна, называется условной функ-

цией распределения F x2 , τ x1 , а p x2 , τ x1 – условной плотно-

стью распределения. Между плотностями распределений вероятностей существуют следующие зависимости:

p(x;y,τ)=p(x)p(y,τ/x)=p(y)p(x/y,τ),

если положить, что x1 = x, x2 = y.

С помощью приведенных распределений можно определить соответствующие математические ожидания. Особый интерес представляют автокорреляционная функция Ψxx(t1,t2)≡M{X(t1)X(t2)} и взаимная корреляционная функция Ψxy(t1,t2)≡ M{X(t1)Y(t2)}. Если случайные сигналы (процессы) удовлетворяют свойству эргодичности (см. далее), то указанные корреляционные функции могут быть представлены также в виде

		τ lim		1	T x t x t τ dt
							x t x t τ ,
	xx
		T 2T
					T
		τ lim		1	T x t y t τ dt
							x t y t τ .
	xy
		T 2T
					T

Заметим, что при = 0 автокорреляционная функция совпадает со средним значением мощности сигнала (процесса): 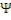xx(0) = x2(t),

а взаимно корреляционная функция представляет собой просто среднее значение произведения двух сигналов x(t), y(t):

Ψxy 0 x t y t τ . Нужно также обратить внимание на то, что все определения даны для случая действительных x(t), y(t).

12

1.2.2. СВОЙСТВА СЛУЧАЙНЫХ ПОТОКОВ ИМПУЛЬСОВ (СЛУЧАЙНЫХ ПРОЦЕССОВ)

Стационарность

Стационарным является поток, для которого никакие его распределения вероятностей не изменятся при замене t на t t0 , например: PN (t0 , t0 t) PN (t) – вероятность появления N событий в

интервале от t0 до t0 t есть функция только N и t; p(τi) = pτ – плотность распределения вероятностей интервалов времени между соседними импульсами не зависит от номера интервала ( i ti ti 1, ti – момент появления i-го импульса).

Последействие

Поток импульсов без последействия характеризуется независимостью появления того или иного числа импульсов в неперекрывающихся временных́ интервалах. Вероятность появления N им-

пульсов в интервале (t0 , t0 t) не зависит от чередования событий

до t0 .

Ординарность

Ординарность потока означает, что вероятность появления двух и более событий за элементарный интервал t пренебрежимо мала по сравнению с вероятностью появления одного события за этот интервал.

Эргодичность

Стационарный случайный поток является эргодическим, если его статистические характеристики при усреднении по числу реализаций и по времени совпадают, например:

1

n

~

1

T

X t

lim

x t

X

lim

x t dt.

0

n n

k

0

T T

k 1

0

Это важно для организации измерений, так как гораздо легче получить одну реализацию случайного процесса на достаточно большом временно́м интервале, чем большое число различных реализаций данного процесса в фиксированный момент времени.

13

Теорема ( соотношения ) Хинчина–Винера

Указанная теорема устанавливает связь между статистическими

и мощностными характеристиками сигналов. В частности, автокорреляционная функция сигнала xx τ и его спектральная плот-

ность мощности Sxx ω связаны прямым и обратным преобразованиями Фурье:

S (ω) 1 ψ (τ)e jωτ dτ;

xx 2π xx

xx (τ) Sxx (ω)e jωτ dω.

Аналогичные соотношения справедливы для взаимной корреляционной функции xy τ двух сигналов x(t) и y(t) и их взаимной

спектральной плотности Sxy ω :

S (ω) 1 ψ (τ)e jωτ dτ;

xy 2π xy

Ψxy (τ) Sxy (ω)e jωτ dω.

1.2.3. ТИПОВЫЕ РАСПРЕДЕЛЕНИЯ И ИХ ХАРАКТЕРИСТИКИ

Биномиальное распределение (распределение Бернулли)

При многократно повторяемых опытах в одинаковых условиях вероятность того, что в результате k опытов событие с вероятностью p появится N раз, определяется формулой Бернулли:

PN CkN pN 1 p k N ,

где CkN k! N! k N ! – число сочетаний из k по N, k и N – целые числа N k . Биномиальное распределение задается двумя

параметрами k и p. Среднее число событий составляет N kp. Дисперсия распределения, т.е. среднее значение квадрата разности

14

между значениями Ni, получаемыми в отдельных сериях из k опытов, и средним значением N равна:

D(N ) σ2 (Ni N )2 kp(1 p) N(1 p).

Относительное среднеквадратичное отклонение составляет:

η	D(N )				(1 p)
					(kp).
		N

Биномиальный закон применяется для описания потоков с ограниченным числом исходных событий (иначе, с ограниченным числом опытов k).

	Распределение Пуассона
При k и	p 0 закон Бернулли в пределе преобразуется
к виду

N e N

PN N N! ,

известному под названием закона Пуассона. Это распределение

имеет только один параметр N , численно равный среднему числу событий за время измерения. Закон Пуассона описывает распределение вероятностей числа появления независимых событий за некоторый интервал времени, если известно среднее число событий за этот интервал.

Для стационарного пуассоновского потока импульсов N nt, где n – интенсивность потока, являющаяся его важнейшей характе-

				1					t const. Для нестационарного потока:
	ристикой: n						NPN
					t
							N 0
			t0 t
		N	n(τ)dτ ,	где n(t) – мгновенная интенсивность потока, равная
			t0					Μ k t,t t
	пределу: n t lim									. Здесь M[k(t,t+ t)] – среднее чис-
					t 0				t

ло событий за интервал от t до t+ t.

Дисперсия распределения в случае пуассоновского потока совпадает со средним числом событий за интервал измерения:

15

D(N ) σ2 N а относительное среднеквадратичное отклонение:

η σ N 1N .

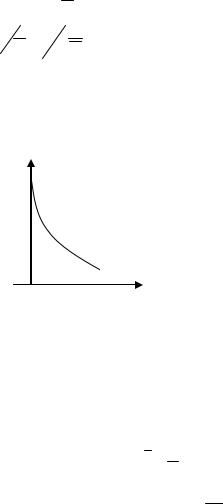
Используя закон Пуассона, можно найти распределение временных́ промежутков между двумя соседними импульсами потока с интенсивностью n. Пусть p( ) – плотность распределения вероятностей интервалов , тогда p( )d – вероятность того, что интервал между произвольной парой соседних импульсов равен с точно-

стью d . Эта вероятность определяется вероятностями двух независимых событий: того, что за время не поступит ни одного импульса, и того, что по окончании за интервал d появится один импульс. Следовательно:

nτ

Рис. 1.5. Распределение временны́х интервалов между соседними импульсами

в пуассоновском потоке

p(τ)dτ P0 (τ)P1 (dτ) e nτ ndτ ,

а плотность распределения вероятностей временных́ интервалов между соседними импульсами:

p(τ) ne nτ .

Вид полученного дифференциального закона представлен на рис. 1.5. Особенность состоит в том, что площадь под кривой распределения равна 1 и наиболее вероятны малые интервалы между импульсами. Основные характеристики распределения:

τ n1 ;

D σ2 n12 ;

η 1.

Поскольку в ядерной электронике распределение Пуассона является наиболее употребимой моделью расположения импульсов на временной́ оси, отметим еще два полезных свойства пуассо-

новских потоков:

16

1) инвариантность относительно операции суммирования (если смешивается k пуассоновских потоков с интенсивностями ni, то результирующий поток также будет пуассоновским с интенсивно-

k

стью n ni );

il

2)инвариантность относительно операции случайного просеивания (если к каждому событию пуассоновского потока, который имеет интенсивность n, применить операцию просеивания, заключающуюся в выбрасывании с вероятностью p события из потока, то оставшийся поток будет пуассоновским с интенсивностью n(1–p), а выброшенные события образуют также пуассоновский поток с интенсивностью np.

Распределение Эрланга

Эрланговы импульсные потоки образуются при детерминированном просеивании пуассоновского потока, заключающемся в выборке из пуассоновского потока каждого k-го импульса. При этом распределение интервалов времени между соседними импульсами в эрланговом потоке имеет вид

pk (τ) nk τk 1 e nτ

(k 1)!

и называется распределением (законом) Эрланга k-го порядка. Очевидно, что k=1 соответствует исходному пуассоновскому потоку. Характеристики распределения:

k

D τ σ2

k

η

σ

1

.

τ

;

;

n

n2

τ

k

Нормальное распределение (закон Гаусса)

В случае нормального (Гауссова) закона распределения некоторой случайной величины X вероятность того, что значение X будет находиться в диапазоне от x до x+dx, определяется выражением

			1			2
	p x dx				exp	x a	dx,
						2D
			2πD

17

где p(x) – плотность распределения вероятностей значений X, a и D – параметры распределения (a – среднее значение X, совпадающее с наиболее вероятным значением; D(x)= 2 – дисперсия).

Надо заметить, что при больших N пуассоновский поток событий, для которого дисперсия равна среднему значению, описывает-

ся также распределением Гаусса, но таким, что D a N :

1

2

p N

exp

N N

.

2πN

2N

Таким образом, при переходе к закону Гаусса определяется не вероятность PN появления N событий за время измерения, а вероятность p(N)dN того, что число событий будет заключено в бесконеч-

но малом интервале от N до

N+dN,

т.е. дискретное распределение

заменяется непрерывным.

Нормальное

распределение

p(U )

является обычной моделью рас-

пределения амплитуд импульсов

1

на выходе детектора, облучаемо-

го моноэнергетическими части-

2

цами:

1

0.61 max

(U U )2

1

2 e

p(U )

exp[

]

σ

2σ2

2π

Напомним, что в пределах ±σ

от среднего находится треть всех

U

U

событий, в пределах ±2σ – 95% и

Рис. 1.6. Распределение амплитуд

в пределах ±3σ – 99,7%.

импульсов на выходе детектора

Учитывая характер

распреде-

ления, естествен вопрос: насколь-

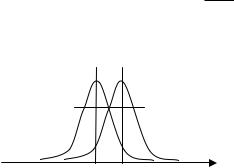
ко близкие значения U1,U 2

можно различить? Принято считать,

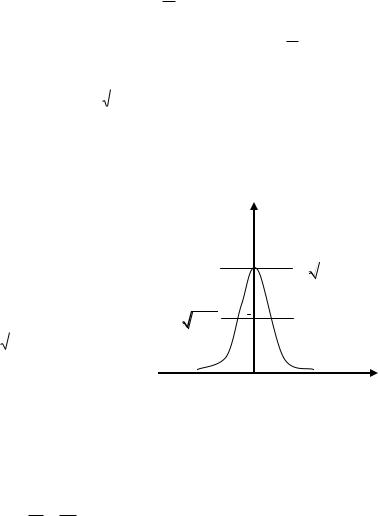
что если кривые распределений пересекаются ниже, чем уровень

0,5 от max, то U1 и U 2 различимы, если выше, то их не различают (рис. 1.7). Таким образом, за амплитудное разрешение детектора

18

принята ширина кривой распределения амплитуд импульсов на полувысоте, если детектор облучался моноэнергетическими частицами:

δA 2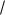2ln2σ 2,36 σ,

а относительное амплитудное

разрешение вводится

как

η

δA

100%

2,36

σ

100%.

A

U

U

0,5 от

Укажем в качестве примера,

что для черенковских счетчи-

max

ηA 4 8 % ,

ков

для

полу-

проводниковых

детекторов

__

__

ηA

0,1%, а для сцинтилляци-

U 1

U 2

Рис. 1.7. Определение амплитудного

онных счетчиков –

12 15 %.

разрешения детектора

ηA

1.3. Основные виды измерений

Ядерная физика – развивающаяся область знания, и число задач, решаемых экспериментальными методами, чрезвычайно разнообразно. В соответствии с этим разнообразием различны и методы, и сами электронные средства измерения. Однако, поскольку полезную информацию несут электрические импульсы, снимаемые с детекторов излучений, то набор величин, доступных для прямого измерения электронными средствами, невелик: амплитуда сигнала, его длительность, длительности фронта, плоской вершины, спада, интервалы между импульсами, очередность появления импульсов, одновременность или некоторая наперед заданная неодновременность сигналов с разных детекторов.

Кроме того, поскольку исследуемые события носят статистический характер, то любой эксперимент включает в себя счет количества полезных событий (набор статистики). Часто ведется абсолютный счет числа событий, что необходимо при последующей обработке результатов измерений, например, для вычитания фона. В некоторых задачах (например, в дозиметрии) нужно определять

19

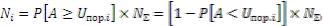
среднее число событий в единицу времени – интенсивность (скорость счета).

Учитывая сказанное, с точки зрения измерительных процедур можно выделить следующие основные виды измерений в экспериментальной практике:

счет числа импульсов и измерение интенсивности импульсных потоков; амплитудные измерения; временные́ измерения.

Широкая распространенность амплитудных измерений связана с тем, что у большинства детекторов амплитуда выходных сигналов пропорциональна энергии зарегистрированной частицы или кванта. Это позволяет, исследуя распределение амплитуд, получить энергетический спектр излучения.

Поскольку измерения обычно ведутся в присутствии фонового излучения (например, космического), а в измерительном тракте присутствуют шумы, то практически всегда используется простейшая процедура амплитудных измерений – амплитудная дискриминация. При этом для последующего анализа в измерительный тракт пропускаются только сигналы, амплитуда которых превышает некоторый установленный порог или находится внутри диапазона, задаваемого двумя порогами – нижним и верхним (рис. 1.8). Собственно пропускание осуществляет схема линейного пропускания (ЛП), а открывается она только на время действия выходного импульса интегрального дискриминатора (рис. 1.8,а) или дифференциального дискриминатора (рис. 1.8,б).

С помощью указанных дискриминаторов можно получить и амплитудные (энергетические) спектры. Если на выходе интегрального дискриминатора подсчитывать при разных порогах (но в течение одинаковых интервалов времени) импульсы, то фактически будет снят интегральный амплитудный спектр (рис. 1.9,а).

Действительно, при некотором установленном пороге Uпор i будет сосчитано число импульсов, превышающих порог,

20