matan

5. lim 3x2 10x 8 . x 4x2 15x 4

Пределы числителя и знаменателя дроби равны . В этом случае говорят, что имеется неопределенность вида «бесконечность на бесконечность». Теорема о пределе частного здесь не применима.

Чтобы раскрыть неопределенность вида			при	x ,

каждый член числителя и знаменателя дроби делят на x в наивысшей степени (в нашем примере на х2), отчего величина дроби не изменится, но исчезнет неопределенность.

lim	3x2	10x 8
x 4x2		15x 4
так как		lim	10
		x x

3x2

10x

8

x

2

x

2

x

2

lim

x

4

15x

4

x2

x2

x2

0; lim	8	0;	lim	15	0;
x x2			x x

3			10			8
				x		x	2			3
lim											,
			15			4
x 4										4
				x		x2

lim 4 0

x x2

(по теореме о связи бесконечно большой и бесконечно малой функций).

Ответ.1.

1

; 2.

14

;

3. 0;

4. ∞;

5.

3

.

3

4

17

Задача. Вычислить пределы:

а) lim

tg3x

;б)

lim

arcsin 6x

.

x 0 ln(1 5x)

x 0

2x

Решение.

tg 3x

tg 0

0

tg 3x ~ 3x;

3x

3

a)

lim

ln(1 5x) ~ 5x

lim

;

ln(1 5x)

x 0

ln1

0

при x

0

x

0 5x

5

arcsin 6x

arcsin 0

0

arcsin 6x ~ 6x

6x

б)

lim

x 0

lim

3.

x 0

2x

0

0

при

x

0

2x

0

В рассматриваемых задачах неопределенность вида

была рас-

0

крыта после замены бесконечно малых функций на эквивалентные им и сокращения полученных дробей на х.

21

	Ответ.а)	3	;	б)3.
	5
					3n 2	4n 1
	Задача. Вычислить предел lim						.
					3n 5
				n
	Решение.Очевидно, что

3n 2

3n 5 5 2

(3n 5) 7

1

7

1

7

.

3n 5

3n 5

3n 5

3n 5

3n

5

Далее воспользуемся вторым замечательным пределом:

3n 2

4n 1

7

4n 1

1

lim

lim

1

3n

n 3n 5

n

5

7

4n 1

4n 1

3n 5 3n 5

7

1

1

lim

1

lim

1

3n 5

3n 5

n

n

7

7

28

7

7 (4n 1)

28n 7

lim

n

5

28

n

lim

3n 5

3 n

lim

e

3n 5

e

n

e

3

.

e

n

28

Ответ.

e

3 .

Производная функции

Задачи 11–20

Найти производные данных функций и их дифференциалы.

11. а) y 3x4	5			2 ;	б) y	2x2
							;
						1 3x
	4
		x

						г) у ln3	(2x х2 ).
в) y 2cos x ln x	1 4x		2	;
						22

12. a) у 5х2 43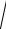x5 3 ;

в) y arctg x4 x ln x .

13. а) y 14 x8 88x3 1;

в) y cos(ln x) x2 tg x .

	14. а) y	1	x5 3x 3				4 ;
						x
		5
					x3 arctg x .
	в) y ln			x 1

15. а) y 3x8 55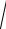x2 3;

в) y tg ex sin x ln x .

16. а) y 5x4		2			3	;
	x		x

в) y ln(sin x) x6 tg x .

	17. а) y 4x3	3			2;
		x 3 x

в) y sin x x ctg x .

18. а) y 7x5 3x 3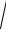x2 6 ;

в) y 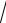ln x (1 2x2 ) sin x .

	19. а) y 3x4	4		3;
		4 x

23

б) y x3 2x ;

3x

г) у tg2 (ex 5x).

б) y 4x2 1 ;

1 x2

г) у cos(x2 3x3).

б) y			x 3			;
			2x 5
г)	у	3 x2				cos 2x.
б) y			3x4		;
			x 3
г)	у	cos2 (x2 9x).

б) y 2x 1; x5

г) у e1 x .

б) y 1 6x2 ;

1 x

г) у arccos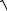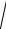4x 6x3 .

б) y 2x 4 ;

1 x2

г) у ln2 (6 3х5 ).

б) y x6 1;

2x 1

u v u v . v2

24

u v u v ;

в) y tg x2 sin x ex .

г)

у

earctg2x.

20. а) y 8x

2

9

6;

б) y

2x2 1

;

x2

x

x

2

1

в) y arcsin x3 ln x cos x.

г)

у

ln(tg5x).

Методические указания к решению задач 11 –20

Производная и дифференциал функции одной переменной

Производной функцииу = f(х) в точке х0 называется предел отношения приращения функции у к приращению аргумента х, при условии, что приращение аргумента стремится к нулю и указанный предел существует:

	y			f(x) f(x0	)
lim	x		lim	x x0				f (x0	)
x 0			x x0

Производная f’(х0)показывает скорость изменения функции f(х)вточке х0. Геометрическиf’(х0)= tg ,где – угол наклона касательной, проведенной к графику функции f(х) в точке х0. Нахождение производной функции f(х) называется еѐ дифференцированием.

Дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной dx= х:

dy f (x)dx.

Правила дифференцирования.Пусть даны дифференцируемые функции u(x) и v (x), тогда справедливы формулы:

u v

u v

u v

uv

u v ;

u v ;

Отметим также, что:

а) производная от независимой переменной равна единице: x 1; б) производная постоянной величины с равна нулю: c 0;

в) постоянный множитель выносится за знак производной:

(cu) c u .

Производная сложной функции.Сложная функция (суперпози-

ция функций) – это функция вида y = f(u), где u = u(x) , то есть этофункция от функции. Например,

функция y sin 2x является сложной, так как ее можно представить в виде y sinu , где u 2x;

функция y etg x является сложной, так как ее можно

представить в виде y eu , где u tg x. Производную сложной функции находят по правилу

f (u(x))

fu

ux .

Таблица производных.

Производные основных

Производные

элементарных функций

cложныхфункций

1

1

u

1. (x )

x

1. (u )

u

1

1

x

u

u

2

x

2

u

1

1

1

1

u

x2

u2

x

u

2. (a

x

a

x

ln a

2. (a

u

a

u

ln a u

)

)

(e

x

e

x

u

u

u

)

(e )

e

1

1

3.

u

(loga x)

x ln a

3. (loga u)

u ln a

1

1

u

u

(ln x)

x

(ln u)

cos x

cosu u

4. (sin x)

4. (sinu)

5.

5.

(cos x)

sin x

(cosu)

sinu u

25

6.					1										6.					1								u
	(tg x)															(tgu)
		cos2 x																cos2 u
7.							1								7.										1							u
	(ctg x)				sin2 x												(ctgu)					sin2 u
							1																		1
															8.																				u
8. (arcsin x)							1 x2									(arcsin u)										1 u2
9.										1					9.														1								u
	(arccos x)							1 x2									(arccosu)											1 u2
							1																		1
10.	(arctg x)				1 x2										10.		(arctgu)					1 u2										u
11.								1							11.													1					u
	(arcctg x)						1 x2										(arcctgu)								1 u2

Задача. Найти производные данных функций и их дифференциалы.

Решение.а) y 4x3		6		3.
		x3
			x

Приведем функцию y к виду, удобному для дифференцирования, используя правила действия со степенями:

	6				6			3 4x3 6x	7
y 4x3				3 4x3
									2 3.
	1				7
	x3 x 2				x 2

По правилу дифференцирования суммы и разности функций:

		6x		7						4x3					6x	7		3
y	4x3
				2 3												2
							7				7	1							9		21
4 3x3 1													0 12x2						2 12x2
			6							x	2							21x							.
							2															x	9

Тогда дифференциал функции y:

26

2

21

dy

f (x)dx

12x

dx .

x

9

б) y

1 9x

.

x3 3

Воспользуемся правилом дифференцирования частного:

u v u v

u

,

где

u 1 9x,

v x3 3.

2

v

v

3

(1 9x) x

3

3

1 9x

1 9x

(x

3)

y

(x3

3)2

x3 3

9 (x3 3) (1 9x) 3x2

9x3

27 3x2 27x3

27 3x2 18x3

.

(x3

3)2

(x3 3)2

(x3

3)2

Тогда дифференциал функции y:

27 3x2

18x3

dy f (x)dx

dx .

(x3

3)2

в) y cos x tg x ln x .

Функция

cos x -

сложная.

Ее можно

представить в виде

1

y u , где

u cos x. Применим формулу

u

u .

2

u

1

sin x

cos x

(cos x)

.

2 cos x

2 cos x

Производную функции tg x ln x находим по правилу дифференцирования произведения:

					u tg x,			v ln x.
	(uv)	u		v u v , где
							1		1
						cos2 x		ln x tg x x .
(tg x ln x)	(tg x)		ln x tg x (ln x)

Таким образом,

27

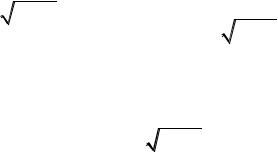
sin x

ln x

tg x

y

cos x

tg x ln x

.

cos2 x

x

2 cos x

Тогда дифференциал функции y:

		sin x				ln x		tg x
dy f (x)dx									dx .
						cos2 x
		2 cos x						x

г) y sin4 (x tg x).

Перепишем данную функцию в виде

y sin4 (x tg x) (sin(x tg x))4.

Функция (sin(x tg x))4 – сложная. Ее можно представить в ви-

де y u4 , где u sin(x tg x).

Применим формулу u4 4u3 u . Тогда

y (sin(x tg x))4 4(sin(x tg x))3 (sin(x tg x)) .

Функция (sin(x tg x)) также сложная. Ее можно представить в

									.
виде sin u , где u x tg x. Применим формулу (sinu)					cosu u
Име-
ем (sin(x tg x)) cos(x tg x) (x tg x) cos(x tg x) 1						1		.
						cos2 x
Таким образом,
						1
y (sin(x tg x))4 4(sin(x tg x))3 cos(x tg x) 1
					cos2 x
Следовательно, дифференциал функции y:
		1
dy 4(sin(x tg x))3 cos(x tg x) 1			dx .
		cos2 x

Приложения производной

Задачи21–30

Исследовать функцию y = f (x) средствами дифференциального исчисления и построить еѐ график.

28

	21.	y		1		x4 x3.				22.	y 2x3 6x2 .
				4
	23.	y 2x3						1	x4 .	24. y x3 6x2 9x.
							2
	25.	y		1			(5x4 x5 ) .			26.	y 2x3 8x2 8x .
				25
	27.	y		1	x4 2x3.					28.	y x3 3x2 .
				2
	29.	y		1			(x5 5x4 ) .			30.	y 2x3 12x2 18x .
				50

Методические указания к решению задач 21 –30

Функция y = f(x) называется чѐтной, если для любых x из области определения функции справедливо равенство f(–x)= f(x), причѐм область определения также симметрична относительно точки 0, в этом случае график функции симметричен относительно оси Oy.

Для нечѐтной функции для любых x из области определения справедливо равенство f(–x)= – f(x), ее график симметричен относительно начала координат.

Функция y = f(x) называется периодической, если существует число T 0 такое, что для любых x из области определения функции справедливо f(x+T)= f(x).

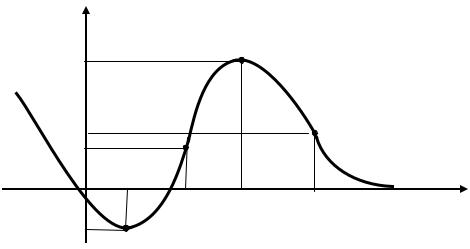
Проиллюстрируем на примере некоторые важные свойства графика функции (рис. 1).

y

C

				D
	B
a	b	c	d	x
A	Рис. 1
	29

Интервалы монотонности:

функция возрастает при x (a;c);

функция убывает при x ( ;a) и x (c; ) .

Точки экстремума: С – точка максимума (max); A – точка минимума (min).

Интервалы выпуклости и вогнутости:функция выпуклая при x (b;d) ;

функция вогнутая при x ( ;b) и при x (d; ) . ТочкиВиDявляются точками перегиба, так как в них происходит

смена выпуклости и вогнутости.

Правило исследования функции y = f(x) на монотонность иточки экстремума.

а) Вычислить первую производную f (x) .

б) Найти критические точки, то есть точки, в которых производная равна нулю или не существует.

в) Определить знак производной на интервалах между критическими точками в области определения функции.

г) Сделать выводы о промежутках монотонности функции со-

гласнопризнакам монотонности:

если f (x) 0 на (a;b), то функция убывает при x (a;b) , если f (x) 0 на (a;b), то функция возрастает при x (a;b) .

д)Сделать выводы о наличии точек экстремума согласнодоста-

точномупризнаку существования экстремума:

если при переходе слева направо через критическую точку x0 производная меняет знак с плюса на минус, то x0 – точка максимума; если с минуса на плюс, то x0 – точка минимума.

Правило исследования функции y = f(x)на выпуклость, вогнутость и точки перегиба.

а) Вычислить вторую производную f (x) .

б) Найти точки, в которых вторая производная равна нулю или не существует, эти точки называются подозрительными на перегиб.

30