matan

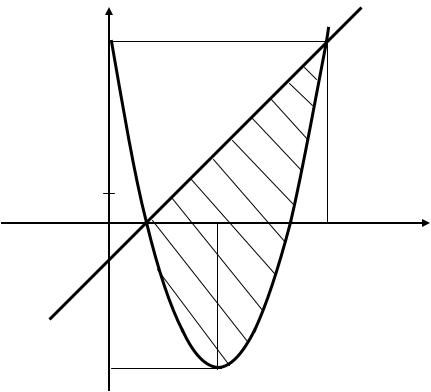
В данной задаче x	6	3,	y 32	6 3 5 4. Итак, верши-
0	2 1		0
на параболы – точка (3;– 4).
Точки пересечения параболы с осями:
С осью Ox: y 0, тогда x2 6x 5 0 . Решив квадратное урав-
нение (прил.1, п. 2), получаем			x1 1,	x2 5 . Точки пересечения

параболы с осью Ox есть точки (1;0) и (5;0).

С осью Oy: x 0, тогда y 02 6 0 5 5 . Точка пересечения параболы с осью Oy есть точка (0;5).

Строим параболу по найденным точкам, замечая, что ветви па-

раболы направлены вверх, т.к. a 1 0		(рис.	10).Прямую y x 1
строим по двум точкам,	например,	при	x 0, y 1; при
x 1 y 0.Получены точки:	(0; 1), (1;0) .

Найдем точки пересечения параболы и прямой, решив систему

уравнений:
	2	6x	5,
y x				x2 6x 5 x			1	x2 7x 6 0.
	1
y x
Решим полученное квадратное уравнение:
D 72 4 1 6 25;					x	7 5	;	x 1; x		6.
					1,2	2		1	2
y
				5

y x 1

1
0	1	3	5 6	x
–1

y x2 6x 5

–4

51

																			Рис.7
Найдем соответствующие ординаты																									y1,2				из уравнения y = x–
1: y1 1 1 0;								y2 6 1 5. Итак,														точки пересечения параболы и
прямой есть точки (1;0) и (6;5) .
Заштрихуем плоскую фигуру, ограниченную параболой и пря-
мой (рис.					7). Здесь функции f (x) x2 6x 5 и																												f		2	(x) x 1 огра-
																			1
ничивают						фигуру						соответственно снизу																	и				сверху,									то есть
f2 (x) f1(x) при x 1;6 .
Для нахождения искомой площади воспользуемся формулой
b														6																		6		x2 7x 6 dx
S ( f2 (x) f1(x)) dx x 1 (x2 6x 5) dx
a														1																		1
		x	3			x	2					6				3				6	2											3								2
				7				6x								6			7				6	6						1					7			1				6 1
		3				2										3				2												3								2
												1
									216							36								1			7									125
														7					36										6											.
									3							2								3			2									6
Ответ. Искомая площадь равна:																							S		125			20					5			кв. ед.
																										6						6

Замечание.Если одна из линий – гипербола, например, xy = –6, то ее можно построить по точкам. Удобно взять точки с абсциссами x 1; 2; 3; и вычислить соответствующие им ординаты y, в

нашем случае по формуле y 6x .

Если в ответе задачи получен логарифм числа, то значение логарифма можно взять из прил.1, п. 9.

Дифференциальные уравнения

Задачи 51–60

Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальному условию y(x0 ) y0.

52

2

3

51. y

x y 2x

;

52. y 2xy xe x2 ;

4

53. y

x y 3x

5;

1

5e5x

54. y

x 2 y x 2 ;

55.y 1 y 1 ;

xx2

56.y y 2ex ;

				2				2
57. y			x 4 y (x 4)						;
58. y y (2x 3)ex ;
				1
59. y				x 1 y 1;

60. y 2 y xe2x ;

х0= 2,

х0= 0,

х0= –2,

x0= 0,

1

х0= 2 ,

х0= 0,

х0= 4,

х0= 0,

х0= 0,

x0= 0,

у0= 0.

у0= –4.

у0= 14 . y0= 32 .

у0= –3.

у0= –3.

у0= 0.

у0= –4.

у0= –4.

y0= –4.

Методические указания к решению задач 51 – 60

Дифференциальное уравнение (ДУ) первого порядка – это урав-

нение вида F(x, y, y ) 0 или y f (x; y) , содержащее производную y от неизвестной функции y y(x).

Решением ДУ называется функция y = y(x), которая при подстановке в уравнение обращает его в тождество.

Например, решением уравнения				2x	является функция
		y
y x2 или	y x2 C ,гдеС – произвольная постоянная. Решением
уравнения		e	x	или	y Ce	x	.
	y y является функция y

Общим решением ДУ называется функция y y(x,C) , зависящая от произвольной постояннойС и удовлетворяющая ДУ при любом значении С.

53

Частное решение получается из общего при конкретных значениях С. Чтобы выделить частное решение из общего задают на-

чальное условие: y y0 при x x0 или y(x0 ) y0.

Совокупность дифференциального уравнения и начального условия

y f (x; y), y(x0 ) y0

называется задачей Коши (для ДУ первого порядка).

Дифференциальные уравнения с разделяющимися переменными.

Дифференциальное уравнение первого порядка вида y h(x)g( y)

называется уравнением с разделяющимися переменными.

Это уравнение можно привести к виду:

P(x)dx Q(y)dy 0 ,

где переменные x и y содержатся в разных слагаемых (разделены). Чтобы разделить переменные нужно производную y предста-

вить как отношение дифференциалов y dydx и выполнить ряд до-

полнительных преобразований (см. примеры ниже).

После разделения переменных производится интегрирование обеих частей равенства. Интегралы берутся с помощью таблицы интегралов с учетом их зависимости от произвольной постоянной

С. Затем, выражая y, находят общее решение ДУ:

y y(x;C) .

Например, найдем общее решение уравнения

2xy .

y

dy

2xy

dy 2xydx

dy

2xdx.

dx

y

Переменные разделились, производим интегрирование.

dy

2xdx

ln

y

2

x2

C0

ln

y

x2 C0;

y

x2 C

x2

2

y

e

y e

C

0

e 0 .

Обозначим

C eC0 , получим

y Cex2

– общее решение

ДУ.

54

Линейные дифференциальные уравнения первого порядка.

ДУ первого порядка называется линейным, если его можно привести к виду: y P(x) y Q(x) , гдеискомая функция y и ее производная y содержатся в первых степенях (в разных слагаемых).

Разделить переменные для такого уравнения не удается, если правая часть Q(x) отлична от нуля.

Линейные ДУ можно решать методом Бернулли. При этом неизвестную функцию y представляют в виде произведения двух функций: y u(x) v(x), для каждой из которых получают ДУ с разделяющимися переменными. Решая первое из этих уравнений, берут его частное решение, например, полагая, чтоС= 0. Для второго уравнения находят его общее решение (с учетом зависимости от

С).

Алгоритм применения метода Бернулли показан ниже на примерах.

Задача. Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальному условию y(x0 ) y0 , если

	а) y 2 y e2x ;									x0 0,	у0 2.
	б) y	4x			y	1			;	x0 1;	y0 2.
		x2	1			x2	1
	Решение.
	а) y 2 y e2x ;		y(0) 2.
	Пусть y uv , тогда
						y	u v uv . Подставим эти выражения в

дифференциальное уравнение:

u v uv 2uv e2x .

Сгруппируем слагаемые, имеющие общий множитель u: u v u v 2v e2x .

Подберем функцию v так, чтобы обратилось в нуль выраже-

ние, стоящее в скобках:

v 2v 0 .

Тогда уравнение примет вид

u v e2x .

55

Два последних уравнения решаются разделением переменных, поочередно.

dv

1.

2v 0;

v

dx

;

v

dv

2v;

dx

dx

dv 2vdx;

|: v 0

dv

2dx;

v

dv

2 dx;

v

ln

v

2x C;

(C 0)

ln v 2x v e2x.

2.Подставим v e2x в

уравнениеu v e2x .

u e2x e2x ; |: e2x 0

	u 1;
	du	1;		dx
	dx
	du dx;

du dx u x C.

Поскольку y = uv, то y = (x+С)e2x – общее решение уравне-

ния.

Для нахождения частного решения обратимся к начальному условию: y0 2при x0 0. Подставим эти значения в общее реше-

ние дифференциального уравнения:

2 (0 C) e0.

Так как e0 1, то

C 2 .

Подставляя найденное значениеС= 2 в общее решение урав-

нения, находим частное решение:

y = (х+2)е2х.

Ответ. у=(х+С)е2х – общее решение уравнения;

у=(х+2)е2х– частное решение уравнения, удовлетворяющее

начальному условию y(0) = 2.

4x

1

б) y

x2 1 y x2 1;

y(1) 2.

Пусть у = uv, тогда y

y и y

в данное

u v uv . Подставим

уравнение:

56

4x

1

x2 1uv x2 1.

u v uv

Группируем 2-е и 3-е слагаемые:

4x

1

u v u v

v

.

x2 1

x2 1

						4x
	Потребуем, чтобы				x2 1v 0			, тогда исходное уравнение
				v
			1
	примет вид:	u v x2 1.

Решим последовательно оба уравнения, причем для первого из них берем лишь частное решение приС= 0.

4x

dv

1. v

v 0

; v

;

x2 1

dx

dv

4x

v;

| dx

dx

x2 1

dv

4x

vdx;

|: v 0

x2 1

dv

4x

dx;

v

x2 1

ln

v

2

2x

dx;

x2 1

ln

v

2

d (x2 1)

;

x2 1

ln

v

2ln(x2 1);

(C 0)

ln

v

ln(x2

1) 2 ;

1

v (x2 1) 2

.

(x2

1)2

2. Подставим

v

1

(x2 1)2

1

в уравнение

u v x2 1.

1

1

u

(x2 1)2 x2 1;

u

1

1;

| (x2 1)

x2 1

2

du

u

x

1;

u

dx

;

du

x2 1;

| dx

dx

du (x2 1)dx;

du (x2 1)dx;

u x3 x C. 3

57

																												x			3									1
	Так как							y uv								,			то y													x C													– общее реше-
																																											2
																													3									x2		1
ние исходного уравнения.
	Для нахождения частного решения обратимся к начальным
условиям: х0= 1;												у0 = 2 – и подставим их в найденное общее реше-
ние:
			3																		1
	2	1					1 C																		;
																							2
			3														12				1
			4									1															4														4					20
	2				C																8										C						C 8												.
			3									4															3														3							3
	Искомое частное решение получим из общего, подставив в не-
																			C			20													x	3					20									1
го найденное значение																											,						y						x													.
																																																			2
																							3											3							3							x2		1
Ответ. y							1									x	3		x C
																									– общее решение уравнения;
		x2 1									2					3
y	1							x	3	x							20
																					– частное решение, удовлетворяющее
	x2 1		2				3											3

начальному условию y(1) = 2.

Замечание. Чтобы проверить правильность найденного решения (общего или частного), нужно подставить его в исходное уравнение и убедиться, что получилось верное равенство (тождество).

Функции нескольких переменных

Задачи 61–70

Для функции z f (x; y) найти: a) полный дифференциал;

б) градиент функции z в точке M (x0; y0 );

58

в) производную функции z f (x; y) в точке

лению вектора								a ax ;ay .
61.	z x2 ln(4x 3y) ,									M(1;–1),
62.	z x3 exy2 ,									M(1;1),
	z 2 y
63.						6x 3y ,				M(2;–1),
64.	z		5y				,			M(0;0),
		x2
					3
65.	z x2 e 3x 2 y ,									M(1;2),
66.	z y ln(x2							y 2) ,		M(2;1),
67.	z xy e2x2 y ,									M(1;1),
68.	z y2 arctg(3x y2 ),									M(3;3),
69.	z				5x y2					M(2;1),
		2y e						,
70.	z			arcsin(x2 2 y),						M(2;–2),
			x

M (x0; y0 ) по направ-

a 3;4 .

a 5;12 .

a 4; 3 .

a 5; 12 .

			4
a 1;				.
			3

a 4;3 .

a 4;3 .

		5
a 6;			.
		2

a 3; 4 .

			5
a 6;				.
			2

Методические указания к решению задач 61 –70

Частные производные, полный дифференциал

Рассмотрим функцию двух переменных z f (x; y) , где x и y – независимые переменные.

Для нахождения частных производных используют таблицу производных и правила дифференцирования для функций одной переменной.

Частная производная по x функции z f (x; y) вычисляется так же, как производная функции одной переменной x в предполо-

59

жении, что y – постоянная величина. Обозначения частной произ-

	z	,	или	f	.
водной по x: zx (x; y) , или	x			x
Частная производная по y			функции z f (x; y) вычисляется

так же, как производная функции одной переменной y в предположении, что x – постоянная величина. Обозначения частной про-

изводной по y:			z	,	или	f	.
		zy (x; y) , или	y			y
Полный дифференциал функции двух переменных находим по
формуле
		dz zxdx zydy ,

где zx , zy – частные производные функции z ; dx и dy – дифференциалы независимых переменных.

Градиент функции, производная по направлению

Вектор – это направленный отрезок. Его можно задать в ко-

ординатной форме:		{ax ;ay}. Числа ax , ay	называются коорди-
	a

натами вектора – это проекции вектора на осиОх иОу соответственно (рис. 8).

y
ay a
0 ax x							Рис. 8
Пусть
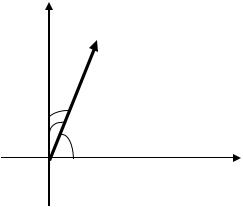
		- это угол между вектором a и положительным на-
правлением осиОх, а					– угол между вектором				и положитель-
								a

ным направлением оси Оу. Косинусы этих углов называются на-

правляющими косинусами вектора a и вычисляются по формулам:

60