заочникам / диф ур / Lecture_on_DE_(full)

1) Матрица системы:	2 0	0
	0 1	−1
A =			.
	0 1	3
Ее характеристическая матрица:	−λ
2		0	0
	0 1 −λ −1
A −λE =				.
	0	1
			3 − λ

Тогда

A − λE = (2 −λ)(λ2 − 4λ + 4) = −(λ − 2)3 ,

λ1,2,3 = 2 .

Итак, имеем характеристический корень кратности l = 3 . При этом

	2 − 2 0		0		0		0	0
	0	1 −	2 −1			0 −1 −1				,
A − 2E =					=
	0	1	3 − 2			0	1	1
r = rang(A − 2E) =1.
Следовательно,		n − r = 3 −1 = 2

идля нахождения решений можно воспользоваться формулами (21.12).

2)Найдем собственные векторы матрицы A , относящиеся к собственному значению λ = 2 . Имеем:

									0	0	0	x
									0	−1	−1	1		= O ,
			(A −2E)X =									x2
									0	1	1	x
												3
		0	0 0 x				0					0 x		−	x		−	x
		0	−1 −1	1			0			или
				x2		=							1	+		2	+	3
		0	1 1	x			0					0 x1			x2			x3
				3

Выбрав x3 в качестве зависимой переменной, а x1, x2

ми, получаем общее решение:

x3 = 0 x1 − x2 .

Находим фундаментальную систему решений:

x1 =1, x2 = 0						x3 = 0 ;
x1 = 0 , x2 =1						x3 = −1.
				1				0
	D1	=		0		, D2		1
							=		.
				0
								−1

=0,

=0.

–свободны-

171

Итак, получили, что D1 , D2 – линейно независимые собственные

векторы матрицы A , относящиеся к собственному значению λ = 2 . Следовательно, решения системы дифференциальных уравнений:

	= e2xD		1				= e2xD			0
Y		= e2x	0		,	Y		2	= e2x	1	.
1	1					2
			0
										−1

3) Третье решение системы уравнений найдем в виде

Y3 = eλx (D30 + D31x) ,

где D31 =α D1 + β D2 , α , β – числа, одновременно не равные нулю, ко-

торые выбираются так, чтобы система линейных уравнений (A −λE)X = D31 была совместна;

D30 – любое решение системы уравнений (A − λE)X = D31 .

Исследуем

на

совместность

систему

линейных

уравнений

(A −λE)X =α D1 + β D2 . Имеем:

x

0

0

0

0 −1 −1

1

(A − 2E)X =

x2

,

0

1

1

x

3

1

0

α

0

1

;

α D1 + β D2 =α

+ β

=

β

0

−1

− β

0 0 0

x

α

0

= α ,

1

β

или

− x2

− x3

=

β ,

0 −1 −1 x2

=

0 x1

0 1 1

x

− β

0 x

+ x

2

+ x

= − β .

3

1

3

Система будет совместна при α = 0

и β . Пусть α = 0

и β = −1.

Тогда

D31 = 0 D1 + (−1) D2 = −D2

и система для нахождения D30

имеет вид

0 x

− x

2

−

x

= −1,

1

3

0

x1

+ x2

+

x3

= 1.

Выбрав x3 в качестве зависимой переменной, а x1, x2 – свободными,

получаем общее решение:

x3 =1 − 0 x1 − x2 .

Полагаем x1 = 0 , x2 = 0 и находим частное решение:

= 0 D30 0 .

1

172

Подставляем D31 = −D2 и D30			в Y3 и получаем:
	0				0					0
Y	= e2x	0		−		1 x		= e2x	− x		.
3
		1
						−1		1		+ x

Найденные таким образом решения Y1 , Y2 , Y3 образуют фундамен-

тальную систему и, следовательно, общее решение системы имеет вид:

Y = C1Y1 + C2Y2 + C3Y3 =

	1						0						0					0
= C e2x 0			+C			2	e2x		1	+C			e2x		0		−		1	x =
1												3
															1
	0								−1										−1
				1							0			e2x				0
	= C e2x			0			+C	2	e2x		1		+C					− x
	1												3
				0
											−1						1 + x

или, более подробно

y1y2y3

=C1e2 x ,

=C2e2 x − C3 xe2 x ,

= −C2e2 x + C3 (1 + x)e2 x .

ПРИМЕР 21.8. Найти общее решение системы Y′ = AY , где

	4	− 4	2
	2	− 2	1
A =				.
	− 4	4	− 2

РЕШЕНИЕ. Так как система – линейная однородная с постоянными коэффициентами, то ее общее решение может быть найдено методом Эйлера.

1) Матрица системы:

						4	− 4	2
						2	− 2	1
		A =							.
						− 4	4 − 2
Ее характеристическая матрица:
					4 −λ		− 4		2
						2	− 2 −λ		1
		A −λE =								.
					− 4		4
									− 2 −λ
Тогда		A −λE		= −λ(λ2 + 4λ − 4λ) = −λ3 ,
					λ1,2,3 = 0 .

173

Итак, имеем характеристический корень кратности l = 3 . При этом

4 −0 − 4			2			4	− 4	2
	2	− 2 −0	1			2	− 2	1		,
A −0 E =					=
	− 4	4	− 2 −0			− 4 4 − 2

r = rang(A −0 E) =1.

Следовательно,

n − r = 3 −1 = 2

идля нахождения решений можно воспользоваться формулами (21.12).

2)Найдем собственный вектор матрицы A , относящийся к собственному значению λ = 0 . Имеем:

4

− 4

2

x

(A −0 E)X =

2 − 2 1

1

x2

= O ,

− 4

4 − 2

x

3

4 − 4 2 x

0

4x

− 4x

+ 2x

= 0,

2 − 2 1

1

0

или

1

−

2

3

x2

=

2x1

2x2

+ x3

= 0,

− 4 4 − 2

x

0

− 4x

+ 4x

− 2x

= 0.

3

1

2

3

Как уже указывали выше, ранг матрицы системы равен 1 и в качестве базисного минора можно выбрать, например, минор 1 . Тогда пе-

ременная x3	будет зависимой, а x1 , x2 – свободными. Отбрасываем пер-
вое и третье уравнение системы и находим общее решение:
	2x1 − 2x2 + x3 = 0 ,
	x3 = −2x1 + 2x2			– общее решение.
Фундаментальная система решений состоит из двух решений. По-
лагая x1 =1,	x2 = 0 и x1 = 0,	x2 =1, находим их:
		1			0
		0			1
	D1 =		,	D2 =		.
		− 2			2

Итак, получили, что D1 и D2 – собственные векторы матрицы A , относящиеся к собственному значению λ = 0 . Следовательно, решение

системы дифференциальных уравнений:
					1							0
Y	= e0 x D	1	=		0		и Y	= e0 x D	2	=		1	.
1							2
					− 2							2

174

3) Третье решение системы уравнений найдем в виде

Y3 = eλx (D30 + D31x) ,

где D31 =α D1 + β D2 , α , β – числа, одновременно не равные нулю, ко-

торые выбираются так, чтобы система линейных уравнений (A −λE)X = D31 была совместна;

D30 – любое решение системы уравнений (A − λE)X = D31 .

Исследуем на совместность		систему			линейных уравнений
(A −λE)X =α D1 + β D2 . Имеем:	4	− 4	2	x
	2	− 2	1		1		,
(A −0 E)X =				x2
	− 4	4	− 2	x
					3

1

0

α

0

1

β

;

α D1 + β D2 =α

+

β

=

2

− 2

− 2α + 2β

4 −4 2

x

α

2 −2 1

1

x2

=

β

.

−4 4 −2

x3

−2α + 2β

Умножим вторую строку на –2 и 2 и прибавим к первой и третьей строке соответственно. В результате получим систему линейных уравнений:

	0	0	0 x				α − 2β
	2 − 2 1			1
				x2		=	β	.
	0	0	0
				x3			− 2α + 4β

Система будет совместна при α −2β = −2α + 4β = 0 , где β – любое действительное число. Пусть

	β =1		α = 2 .
							2
Тогда	D31 = 2 D1		+ D2				1
					=
							− 2
и система для нахождения D30		имеет вид
	{2x	− 2x	2	+ x	3	= 1,
	1

Выбрав x3 в качестве зависимой переменной, а x1, x2 – свободными,

получаем общее решение:

x3 =1−2x1 + 2x2 .

175

Полагаем x1 = 0 , x2 = 0 и находим частное решение:

		0
D30		0
	=		.
		1

Подставляем D31 = 2 D1 + D2		и D30			в Y3 и получаем:
	0				2					2x
Y	= e0 x	0		+	1	x		=		x	.
3
									1	−2x
		1			−2
Найденные таким образом решения Y1 , Y2 , Y3											образуют фундамен-

тальную систему и, следовательно, общее решение системы имеет вид:

						Y = C1Y1 + C2Y2 + C3Y3 =
	1			0			0			2				1			0			2x
	0					+C3		0		1				0						x
= C1			+C2	1					+		x		= C1			+C2	1		+C3
	−2							1		−2				− 2
				2													2		1	− 2x

или, более подробно

y1y2y3

=	C1	+ 2C3 x,
=	C2	+	C3 x,
= − 2C1 +			2C2 + C3 (1 − 2x).

Итак, мы рассмотрели метод Эйлера в трех случаях:

1)характеристические корни матрицы A действительны и различны;

2)характеристические корни матрицы A различны, но среди них есть комплексные;

3)характеристические корни матрицы A действительны, но среди них есть кратные.

Не рассмотренным остался случай, когда среди характеристических корней матрицы A есть кратные комплексные корни. В этой ситуации алгебраические трудности метода Эйлера возрастают настолько, что лучше использовать другие методы интегрирования.

176

§ 22. Линейные уравнения с частными производными первого порядка

22.1.Понятие уравнения с частными производными

иего интегрирование

Уравнением с частными производными1 называется соотноше-

ние, связывающее неизвестную функцию нескольких переменных, ее аргументы и ее частные производные. Порядок старшей частной производной, входящей в уравнение, называется порядком уравнения.

Функция, обращающая уравнение с частными производными в тождество, называется решением этого уравнения. Процесс нахождения решений дифференциального уравнения с частными производными называется интегрированием этого уравнения.

Так как обыкновенные дифференциальные уравнения можно рассматривать как частный случай уравнения с частными производными, то можно утверждать, что если уравнение с частными производными имеет решение, то решений будет множество.

Для обыкновенных дифференциальных уравнений порядка n вся совокупность решений (за исключением некоторых) представлялась функцией, зависящей от независимой переменной x и n произвольных постоянных C1, C2 , … , Cn (общим решением)2. Для дифференциаль-

ных уравнений с частными производными общее решение будет иметь более сложную структуру. Оно тоже будет содержать некоторые произвольные элементы, но это уже будут не константы, а функции. В этом можно убедиться, рассмотрев несколько простых примеров.

ПРИМЕРЫ.

1)Рассмотрим уравнение F (x, y, z, z′x ) = 0 , где z = z(x, y) .

Это уравнение можно рассматривать как обыкновенное дифференциальное уравнение относительно x , где y – параметр. Общее решение

такого уравнения будет иметь вид

z =ϕ(x, y,C( y)) ,

где C( y) – произвольная функция.

1	Или «уравнением в частных производных».
2	Справедливо и	обратное. Т. е. для любого семейства функций
	y =ϕ(x,C1,K,Cn )	существует дифференциальное уравнение порядка n , для
	которого это семейство является общим решением. Оно получается в результате

		y =ϕ(x,C ,K,C					) ,
		′	=ϕ	′	1	n		) ,
		y		(x,C ,K,C
исключения констант C1	,K,Cn из системы				1	n
	KKKKKKKKKK
		(n)	=ϕ	(n)	(x,C1	,K,Cn ).
	y

177

2)Рассмотрим уравнение z′x = z′y , где z = z(x, y) . Введем новые переменные по формулам

	u = x + y ,							v = x − y .
Тогда		z(x, y) = f (u, v) ,
z′x = fu′ u′x + fv′ v′x = fu′ + fv′,
			{					{
				1				1
z′y = fu′ u′y + fv′ v′y = fu′ − fv′.
			{					{
				1				−1
Из уравнения z′x = z′y получаем:
		fu′ + fv′ = fu′ − fv′,
			2 fv′ = 0 ,
f (u, v) =ϕ(u)							или	z(x, y) =ϕ(x + y) ,
где ϕ(x + y) – произвольная функция.
3) Рассмотрим уравнение	∂2 z			= 0 , где z = z(x, y) .
	∂x∂y
		∂2 z				=	∂z	∂z
Имеем:								= 0 ,
		∂x∂y
							∂y	∂x

∂∂xz – не зависит от y ,

∂∂xz =ϕ(x) , где ϕ(x) – произвольная функция;

z = ∫ϕ(x)dx +ψ ( y) = ω(x) +ψ( y) ,

где ω(x),ψ ( y) – произвольные функции.

4) Рассмотрим уравнение ∂2 z = 0 , где z = z(x, y) .

∂x2

Имеем:	∂2 z		=	∂z	∂z	= 0,
	∂x	2
				∂x	∂x

∂∂xz – не зависит от x ,

∂∂xz =ϕ( y) , где ϕ( y) – произвольная функция;

z = ∫ϕ( y)dx +ψ ( y) =ϕ( y)x +ψ ( y) ,

где ϕ( y),ψ( y) – произвольные функции.

178

Как показывают рассмотренные примеры, уравнение с частными производными имеет множество решений, которые определяются с точностью до некоторой функции. Поэтому, для выбора одного решения необходимо задавать некоторые условия, которым эта функция должна удовлетворять.

Если уравнение можно разрешить относительно старшей частной производной, т. е. записать, например, в виде

∂

m

z

∂

k

z

=

f x , x

,K, x

n

, z,

,K

,

(22.1)

∂xm

∂xk1

K∂xkn

1

2

1

1

n

здесь k1 +K+ kn = k ≤ m и k1 < m , то обычно полагают, что

	z				x	=x		=ϕ0 (x2 ,K, xn ),
	∂z				1	10
								=ϕ1 (x2 ,K, xn ),
	∂x1				x1	=x10
										(22.2)
	. . . . . . . . . . . . . . . .
	∂m−1z
	∂xm−1							=ϕm−1 (x2 ,K, xn ),
							x	=x
	1						1	10

где x10 – заданное значение, ϕ0 (x2 ,K, xn ) , …, ϕm−1 (x2 ,K, xn ) – заданные функции n −1 аргумента. Условия (22.2) называют начальными условиями для уравнения (22.1), а задача нахождения решения уравнения (22.1), удовлетворяющего начальным условиям (22.2), называется задачей Коши.

В частности, для уравнения первого порядка

∂z

∂z

∂z

(22.3)

=

f x1

, x2

,K, xn , z,

,K,

∂x

∂x

2

∂x

1

n

начальное условие будет иметь вид

z

x =x

=ϕ0 (x2 ,K, xn ) ,

(22.4)

1

10

где x10 – заданное значение, ϕ0 (x2 ,K, xn ) – заданная функция n −1 ар-

гумента.

В случае функции z = z(x, y) задача Коши для уравнения с частными производными первого порядка имеет простой геометрический

смысл. Действительно, для уравнения	∂z	=		∂z
			f x, y, z,		частное реше-
	∂x			∂y

ние z =ϕ(x, y) представляет собой некоторую поверхность в пространстве Oxyz (ее называют интегральной поверхностью). Тогда, общее

179

решение – некоторое семейство поверхностей. Начальное	условие
z(x = x0 , y) = ϕ0 ( y) задает в пространстве некоторую кривую	x = x0 ,

z( y) =ϕ0 ( y) . Следовательно, задача Коши представляет собой на-

хождение поверхности, проходящей через заданную кривую.

Например, если общее решение z =ϕ(x2 + y2 ) – семейство поверх-

ностей вращения (рис. 22.1), то частным решением будет та поверхность, на которой лежит заданная кривая (начальное условие z(x = x0 , y) = ϕ0 ( y) ). Так на рис 22.1 в качестве начального условия вы-

брана ветка гиперболы z(x = x0 , y) = x02 + y2 и, следовательно, частным решением является конус, на поверхности которого она лежит.

z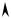

x0

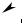
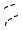
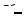
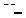
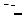
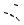
x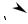y

Рис. 22.1.

По аналогии с трехмерным пространством, говорят, что (x1, x2 ,K, xn , z) – точка n +1-мерного пространства, z =ϕ(x1, x2 ,K, xn ) – гиперповерхность (поверхность n измерений) в n +1-мерном пространстве, а условие

z(x1 , x2 ,K, xn ) x1 =x10 =ϕ0 (x2 ,K, xn )

определяют в n +1-мерном пространстве гиперповерхность n −1-из-

мерения. Поэтому говорят, что для дифференциального уравнения с частными производными первого порядка задача Коши в общем случае состоит в нахождении интегральной гиперповерхности, проходящей через заданную гиперповерхность n −1-измерения.

В нашем курсе мы будем рассматривать только линейные уравнения с частными производными первого порядка, поскольку их интегрирование сводится к интегрированию некоторой системы обыкновенных дифференциальных уравнений.

180