заочникам / диф ур / Lecture_on_DE_(full)

Тогда свободной переменной является y, а искомая функция x=x( y ).

Полагаем

x

= z ,

y

x = z y ,

x′ = z + y z′.

Подставляя в уравнение выражения для x и x′

получаем

z + yz

′

=

2z 2 −2z + 2

,

1−4z

yz

′

6z2

−3z + 2

=

1−4z .

Разделяя переменные и интегрируя, находим

1−4z

dz =

dy

или

1 d (6z 2 −3z + 2)

= −

dy

,

6z 2 −3z + 2

y

3 6z 2 −3z + 2

y

ln(6z2 −3z + 2) = ln C3 −ln | y3 |, С > 0;

6z

2

−3z

+ 2 =

C3

, C ≠0 .

y3

Подставляя		x	= z , получаем общий интеграл
		y
			6x2 y −3xy2 + 2 y3 = C3 , C ≠0 .
Потери решений в процессе интегрирования не произошло, так как
6z2 −3z + 2	≠ 0 , z , а y = 0 не является решением.

§ 6. Уравнения, приводящиеся к однородным

	′		a1x+b1 y+c1
	6.1. Уравнение вида y	= f a			x+b	y+c
				2	2		2

	Рассмотрим уравнение
	′		a1x+b1 y+c1
									(6.1)
	y	= f a		2	x+b	y+c	2	.
					2

Если c1 =c2 =0 , то уравнение (6.1) будет однородным. В противном случае, в зависимости от коэффициентов при x и y , оно может быть с

помощью замены приведено либо к уравнению с разделяющимися переменными, либо к однородному. Рассмотри каждый из этих двух случаев.

21

1) Пусть хотя бы одно из чисел c1 или c2 фициенты при x и y удовлетворяют условию

a1		b1	≠ 0 .
a	2	b
		2

Тогда система уравнений

a1x + b1 y + c1 = 0,

a2 x + b2 y + c2 = 0

будет иметь единственное решение. Сделаем замену переменных:

отлично от нуля, а коэф-

(6.2)

x =t +α , y =z+β ,

где α и β – решения системы (6.2). Тогда

dy =dz

и из уравнения (6.1)

получим:

dx

dt

dz

a1 (t +α)

+b1 (z+β)+c1

dt

= f

,

a

2

(t +α)+b (z+

β)+c

2

2

dz

a1t +b1 z

+(a1α +b1β

+c1 )

dt

= f

.

a

2

t +b z

+(a α +b β

+c

2

)

2

2

2

Но α и β – решения системы (6.2). Следовательно,

a1α +b1β +c1 = 0 и a2α +b2 β +c2 = 0 ,

и имеет место однородное уравнение

dz

a1t +b1 z

dt

= f

.

a

t +b z

2

2

2) Теперь рассмотрим случай, когда хотя бы одно из чисел c1 или c2 отлично от нуля, а коэффициенты при x и y удовлетворяют условию

a1		b1	= 0 .
a	2	b
		2

Равенство нулю определителя второго порядка с ненулевыми элементами означает, что его строки пропорциональны, т. е.

		a2 =λa1 ,			b2 =λb1 .
Но тогда уравнение (6.1) можно записать в виде
′		a1x+b1 y+c1			′
						=ϕ(a1x+b1 y) .
		λ(a x+b y)+c
y	= f				или y
		1 1	2

22

Это уравнение вида (4.2), которые мы уже рассмотрели ранее в §4. Мы показали, что оно приводится к уравнению с разделяющимися переменными с помощью замены z =a1x+b1 y .

ПРИМЕР 6.1. Найти общий интеграл уравнения

(4 y −3x −5) y′−3y +7x +2 = 0 .
РЕШЕНИЕ. Запишем уравнение в виде
−7x +3y − 2
y′ = −3x + 4 y −5 .
Это уравнение вида (6.1). Рассмотрим систему
−7x +3y −2 = 0,
			= 0.
−3x + 4 y −5
Она имеет единственное решение
x0 =	7	, y0 =	29 .
19			19

Следовательно, уравнение приводится к однородному заменой

x = t + x0 = t +

7

,

y = z + y0 = z +

29 .

19

19

В результате получим однородное уравнение

dz

=

− 7t + 3z

.

dt

− 3t + 4z

Сделаем еще одну замену переменных:

z = ut

dz = u + t du .

Это приведет нас к уравнению

dt

dt

u + t du

=

− 7 + 3u

,

− 3 + 4u

dt

t

du

= − 4u2 + 6u − 7 .

dt

− 3 + 4u

Это уравнение с разделяющимися переменными. Запишем его в виде

dt	+			4u	− 3	du = 0 ,
t			4u2 −		6u + 7
dt		+		1 d (4u2 −6u+7)			=0 .
	t			2 4u2 −6u+7

Интегрируя, получаем

23

1

2

~

~

ln

t

+ 2 ln(4u

−6u +7) = ln C ,

C > 0 ;

~2

~

(4u

2

−6u

+7) t

2

,

> 0 ;

= C

C

(4u2 −6u +7)t 2 = C , C >0 .

Сделаем обратную замену переменных u =

z

и получим:

t

Но z = y−29

7

4z2 −6zt +7t 2 =C , C >0 .

, t =x−

. Следовательно

19

19

7x2 + 4 y2 −6xy + 4x −10 y = C −131 .

19

Переобозначив C −

131 через C , окончательно получим

19

7x2 +4 y2 −6xy+4x−10 y =C , где C > −13119 .

Потери решений в процессе интегрирования не произошло, так как 4u2 −6u +7 > 0 u , а t = 0 не является решением.

ПРИМЕР 6.2. Найти общий интеграл уравнения

(x + 2 y +1) y′ = 2x + 4 y +3.

РЕШЕНИЕ. Запишем уравнение в виде

y′ = 2x + 4 y +3 . x + 2 y +1

Это уравнение вида (6.1). Рассмотрим систему

2x + 4 y +3 = 0,

x + 2 y +1 = 0.

Так как определитель ее матрицы 12 42 = 0 , то система не имеет решений

и исходное дифференциальное уравнение сводится к уравнению с разделяющимися переменными с помощью замены

z = x + 2 y .

В этом случае имеем: z′ =1+ 2 y′,

y′ = 12 (z′−1) ,

и из уравнения получаем:

24

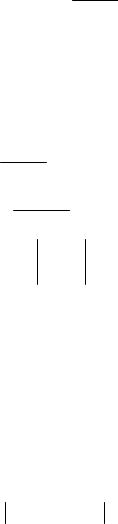
12 (z′−1)= 2zz++13 .

Разделяя переменные и интегрируя, находим:

dz	=	4z + 6			+1 или		dz	=	5z + 7	,
dx			z +1				dx		z +1
			z +1			dz = dx (5z +7			≠ 0) ,
			5z +7

∫5zz++17 dz = ∫dx +C ,

15 ∫ 1− z +2 /75/ 5 dz = ∫dx +C ,

z − 52 ln z + 75 = 5x +C .

Заменяя z = x + 2 y , получаем:

x + 2 y −		2 ln				x + 2 y +		7			= 5x +C ,
		5						5
2 y −		2 ln				x + 2 y +		7			= 4x +C ,
		5						5
y −	1 ln			x + 2 y +			7				= 2x +C ,
	5						5

5 y −ln 5x +10 y +7 =10x +C .

В процессе интегрирования, при делении на 5z + 7 , было потеряно решение 5x +10 y +7 = 0 . Оно может быть включено в общий интеграл,

если переписать общий интеграл в виде:

5x +10 y +7 = Ce5 y−10 x , C.

6.2. Обобщенно однородные уравнения

Уравнение первого порядка называется обобщённо однородным, если существует такое рациональное число α , что каждое слагаемое уравнения – однородная функция степени m относительно x , y , y′

(относительно x , y , dx , dy ), если считать x – величиной измерения 1, y – величиной измерения α , y′( dy ) – величиной измерения α−1, dx – величиной измерения 0.

25

Иначе говоря, уравнение P(x, y)dx +Q(x, y)dy = 0 является обоб-

щено однородным, если существует такое рациональное число α , что

P(tx, tα y)dx +Q(tx, tα y) (tα−1dy) = t m [P(x, y)dx +Q(x, y)dy]

или, что тоже, выполняются равенства

P(tx,tα y)dx = t m P(x, y)dx ,		(6.3)
Q(tx,tα y) (tα−1dy) = t m Q(x, y)dy.

Обобщенно однородное уравнение приводится к однородному уравнению заменой

y =zα .

Действительно, после замены y = zα получим уравнение
P(x, zα )dx +Q(x, zα ) αzα−1 dz = 0 .		(6.4)
14243	1442443
P1 ( x,z)	Q1 ( x,z)

Рассмотрим функцию P1 (x, z) . Имеем:

P1 (tx, tz)dx = P(tx, (tz)α )dx = P(tx, tα zα )dx = P(tx, tα y)dx .

По условию (6.3)

P(tx, tα y)dx = t m P(x, y)dx .

P1 (tx, tz)dx = t m P(x, y)dx = t m P(x, zα )dx = t m P1 (x, z)dx ,

P1 (tx, tz) = t m P1 (x, z) .

Аналогично, для Q1 (x, z) , имеем:

Q1 (tx,tz)dz = Q(tx, (tz)α ) α(tz)α−1 dz = Q(tx,tα zα ) tα−1 αzα−1dz = = Q(tx,tα y) tα−1 dy

По условию (6.3)

Q(tx,tα y) (tα−1dy) = t m Q(x, y)dy .

Q1 (tx,tz)dz = t mQ(x, y)dy = t m Q(x, zα ) αzα−1dz = t m Q1 (x, z)dz ;

Q1 (tx, tz) = t mQ1 (x, z) .

Итак, функции P1 (x, z) и Q1 (x, z) – однородные одинаковой степени и, следовательно, уравнение (6.4) – однородное.

Обобщенно однородное уравнение приводится к уравнению с разделяющимися переменными заменой

y =zxα .

26

Действительно, из определения обобщенного однородного уравнения, получаем:

P(tx, tα y) = t m P(x, y)

и Q(tx,tα y) = t m−α+1Q(x, y) .

Положим t = 1 . Тогда:

x

y

1

α

P(tx, t

y) =

P 1,

=

P(x, y) ,

xα

xm

α

y

1

Q(tx, t

y) = Q 1,

=

Q(x, y) .

xm−α+1

Следовательно,

xα

y

y

m

m−α+1

P(x, y) = x

P 1,

,

Q(x, y) =

x

Q 1,

xα

xα

P(x, y)

= xα

−1

y

−

ϕ

.

Q(x, y)

xα

Таким образом, обобщенно однородное уравнение, разрешенное

относительно производной, имеет вид

y′

P(x, y)

= x

α−1

y

= −

ϕ

Q(x, y)

xα

Делая в этом уравнении замену y =zxα получим:

′

α

+ z α x

α−1

=

x

α−1

ϕ(z) ,

z x

′

=ϕ(z) −αz .

z x

Но последнее уравнение, очевидно, является уравнением с разделяющимися переменными.

	2		2
ПРИМЕР 6.3. Найти все решения уравнения		− y		dx + dy = 0 .
x2

РЕШЕНИЕ. Запишем уравнение в виде

x22 dx − y2 dx + dy = 0 .

Слагаемое x22 dx имеет измерение 1 (−2) + 0 = −2 , слагаемое y2dx – из-

мерение α 2 + 0 = 2α , слагаемое dy – измерение α −1. Равенства

− 2 = 2α =α −1

справедливы при α = −1. Следовательно, данное уравнение – обобщённо однородное, α = −1.

27

Приведем исходное уравнение к уравнению с разделяющимися переменными, сделав замену y =zx−1. Тогда:

= dz − zdx dy x x2 ,

и уравнение примет вид:
2		dx −	z2	dx +	dz	−	zdx	= 0		или
	x2		x2		x		x2
						dx			+	dz
										2 − z − z2
							x

(2 − z − z2 )dx + xdz = 0 ,

= 0 ,

dx

1

1

1

dx

1

1

+

−

dz = 0

или 3

+

−

dz = 0 .

x

3

z −1

x

z −1

z + 2

z + 2

Интегрируя, находим

dx

1

1

3∫

+ ∫

−

dz = ln C , C >0 ,

x

+ 2

z

z

−1

3 ln

x

z + 2

= ln C , C >0 ,

+ ln

z −1

z −1

= Cx3

3

= Cx3

, C ≠0 ,

или

1 −

z + 2

z +

2

3

z + 2

=

, C ≠0 ,

1

−Cx3

z =

1+ 2Cx3

, C ≠0 .

1−Cx3

Сделаем обратную замену переменных z = yx и получим:

yx =

1

+ 2Cx3

,

C ≠0 ,

1−Cx3

y =

1+ 2Cx3

, C ≠0 .

x −Cx4

В процессе преобразований было потеряно решение y = x−1 (т. е. z =1). Оно может быть включено в общее при C = 0 . Решение y =−2x−1

(т. е. z = −2 ) входит в общее при C1 = 0 , т. е. при C = ∞.

Таким образом, все решения уравнения имеют вид:

	y =	1 + 2Cx3	, C .
		x −Cx4

28

§ 7. Линейные уравнения первого порядка

Линейным дифференциальным уравнением первого порядка на-

зывается уравнение, которое может быть записано в виде

y′+ p(x) y = f (x) ,	(7.1)

где p( x), f (x) – заданные непрерывные функции.

Иначе говоря, линейное дифференциальное уравнение первого порядка это уравнение, в которое неизвестная функция y и ее производ-

ная y′ входят в первых степенях и не перемножаясь1.

Если f (x) ≡ 0 , то линейное уравнение называется однородным. В

противном случае уравнение называется неоднородным. Рассмотрим их по отдельности.

7.1. Линейные однородные уравнения

Линейное однородное уравнение

y′+ p(x) y = 0	(7.2)

является уравнением с разделяющимися переменными.

Действительно, разделяя переменные, получаем

dy

+ p(x)dx = 0

(где

y ≠ 0 ).

y

Откуда находим

ln

y

+ ∫ p(x)dx = ln C , C > 0

(здесь для удобства постоянная С представлена в виде ln C );

y

e

∫p(x)dx

= C ,

y = C e−∫p(x)dx ,

C ≠ 0 .

(7.3)

В процессе преобразований было потеряно решение y = 0 . Оно

может быть получено по формуле (7.3) при C = 0 . Следовательно, общее решение линейного однородного уравнения (7.2) будет иметь вид

y = C e−∫p(x)dx , C .

(7.4)

1 Т. е. линейное относительно неизвестной функции и ее производной.

29

7.2. Линейные неоднородные уравнения

Имеются два метода интегрирования линейных неоднородных уравнений первого порядка.

1) Метод вариации постоянной (метод Лагранжа).

Сначала решаем однородное уравнение, которое имеет ту же левую часть, что и уравнение (7.1) (его называют однородным уравнением,

соответствующим данному неоднородному уравнению). Общим ре-

шением такого уравнения, как было показано выше, является функция

y = C e−∫ p( x)dx .

Далее полагаем, что решение неоднородного уравнения по структуре совпадает с решением соответствующего линейного однородного уравнения, т. е. имеет вид

y = C(x) e−∫ p( x)dx .

Функцию C(x) можно найти, подставив y и y′ в исходное неоднородное уравнение (7.1). Действительно,

y′ =	dy dC	e	−∫ p( x)dx		−C(x) e		−∫	p( x)dx	p(x) .
	dx = dx
Подставляя выражения для y и y′ в (7.1) получим
dC e−∫ p( x)dx	−C(x) e−∫ p( x)dx p(x) + p(x) C(x) e−∫ p( x)dx = f (x) ,
dx	dC e−∫p( x)dx = f (x) ,
		dx
	dC			= f (x) e∫p(x)dx ,
			dx
	dC = f (x) e∫ p(x)dxdx .
Интегрируя, находим
				(x) e		∫p(x)dx		+C1 .
	C(x) = ∫ f					dx

И, окончательно получим, что общее решение неоднородного уравнения имеет вид

		∫p(x)dx		e	−∫p(x)dx
y(x) =	∫ f (x) e	dx +C1

или

y(x) = C1 e−∫p(x)dx + e−∫p(x)dx ∫ f (x) e∫p(x)dx

	(7.5)
dx .

30