Тема 6: Функция распределения случайной величины. Нормально распределенные случайные величины.

Пусть X случайная величина на пространстве элементарных событий с алгеброй случайных событий.

Определение. Функцией распределения случайной величины X называется функция , определяемая равенством

В дальнейшем будем использовать следующие обозначения:

Аналогично определяются вероятности

Сформулируем без доказательства основные свойства функции распределения.

не убывает.

То есть непрерывна слева.

Заметим, что свойство является очевидным следствием свойства.

Задача. Доказать свойства

Если X дискретная случайная величина с таблицей распределения (2), то не трудно построить график ее функции распределения

Графиком является ступенчатая функция, изображенная на рисунке. Из этого графика видно, что закон распределения случайной величины можно найти через значения функции распределения:

где (или, если- наибольшее значениеX).

Таким образом, дискретная случайная величина полностью определяется своей функцией распределения.

Непрерывная случайная величина.

Определение. Случайная величина X называется непрерывной, если ее функция распределения непрерывна при всех.

Утверждение. Если X непрерывная случайная величина, то , то есть вероятность каждого отдельного значения непрерывной случайной величины равна 0.

Доказательство.

Легко видеть, что

Утверждение доказано.

Определение. Пусть функция дифференцируемая на всей, за исключением, быть может, конечного или счетного множества точек. Плотностью вероятности случайной величиныX называется функция

Для большинства непрерывных случайных величин имеет место формула

(9)

где справа в формуле стоит несобственный интеграл.

Задача. Доказать формулу (9) в случае, когда непрерывна на.

Из свойств функции распределения вытекают следующие свойства плотности вероятности.

Если есть плотность вероятности непрерывной случайной величиныX, то

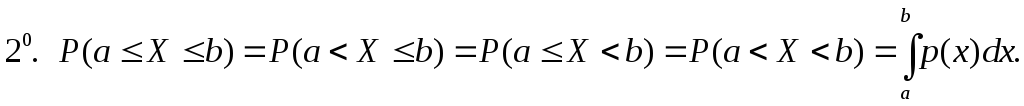
Примеры непрерывных случайных величин. Равномерное распределение на отрезке.

Определение. Случайная величина X называется равномерно распределенной на отрезке , если она имеет плотность вероятности следующего вида:

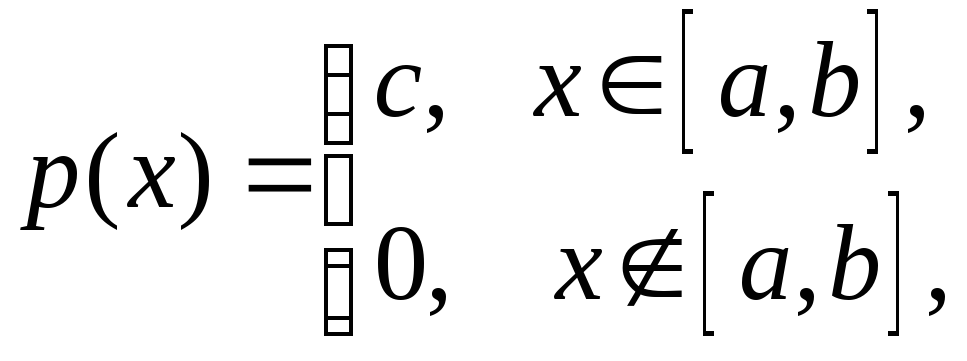
где Графикизображен на рисунке.

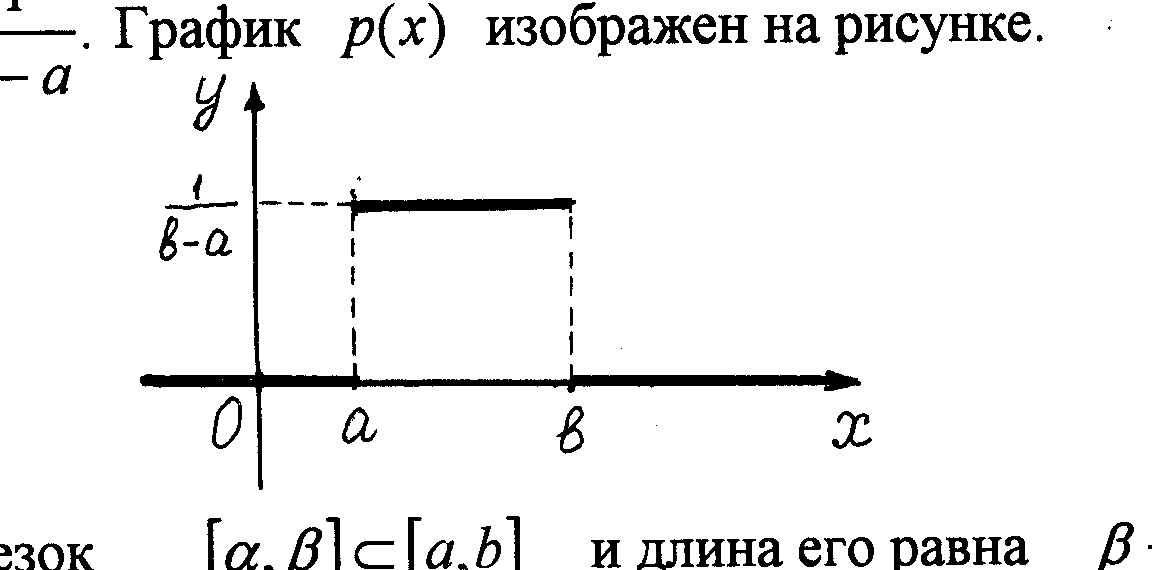
Пусть отрезок и длина его равнаТогда

Таким образом, вероятность попаданий значений X в любую часть отрезка пропорционально длине этой части.

Приведем пример равномерно распределенной случайной величины.

Пусть есть интервал движения между троллейбусами на городской линии. Пусть случайная величинаX равна времени ожидания троллейбуса на остановке. Случайная величина X равномерно распределена на отрезке

Нормально распределенная величина.

На практике широко распространены случайные величины, плотность распределения вероятности которых определяется функцией

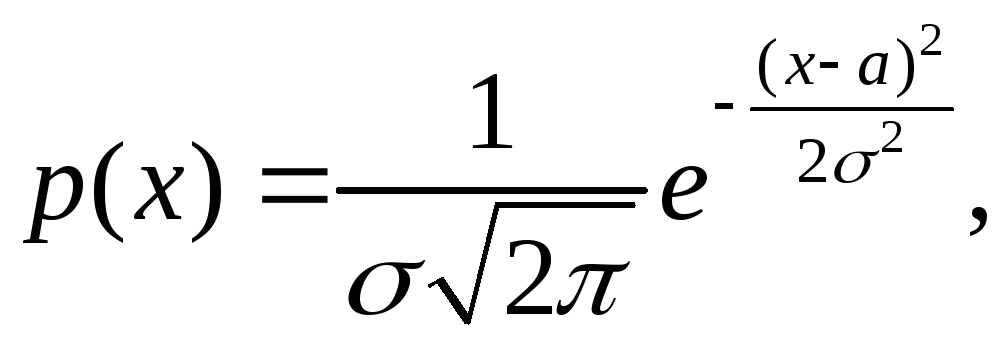
где и- некоторые постоянные числа и. В этом случае говорят, что случайная величинаX распределена по закону Гаусса или по нормальному закону.

Утверждение. Плотность вероятности нормально распределенной случайной величины удовлетворяет свойству .

Доказательство.

.

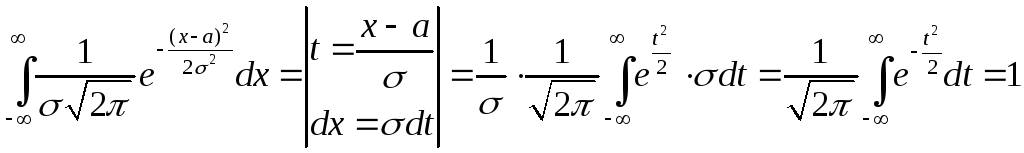(см. замечание на стр. 18). Утверждение доказано.

Если X есть нормально распределенная величина с параметрами и, то говорят, чтоX распределена по закону

График плотности вероятности нормального распределения называют нормальной кривой.

Он симметричен относительно прямой и придостигает максимума. При увеличениикривая становится более пологой. На рисунке представлены нормальные кривые приПри любомплощадь под кривой, согласно свойства, равна 1.

Задача. Доказать, что точки являются точками перегиба.

Утверждение. Если X распределена по закону , то

(10)

где есть функция Лапласа, определенная на стр. 62.

Доказательство.

=

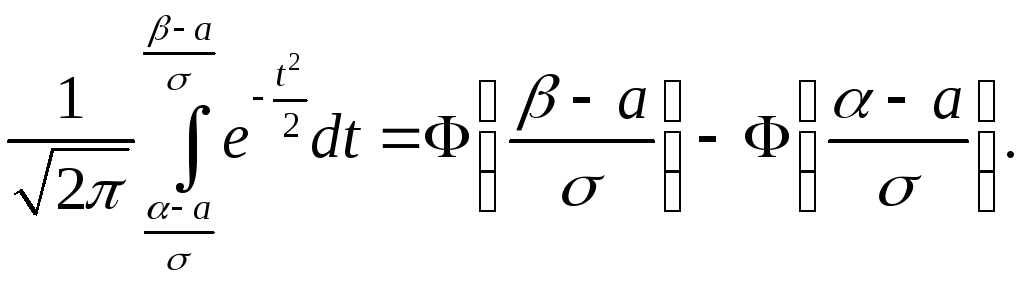
Утверждение доказано.

Следствие. Если X распределена по закону , то

(11)

Доказательство.

Согласно (10)

где найдено по таблице.

Утверждение доказано.

Таким образом, событие, состоящее в том, что является практически достоверным. Это правило называется«правилом трех сигм».

Нормально распределенные случайные величины играют важную роль в теории вероятностей. Дело в том, что распределение многих случайных величин, встречающихся в жизни, близко к нормальному распределению. Этот факт является следствием Центральной предельной теоремы теории вероятностей, которую доказал в 1901 году выдающийся русский математик А.М. Ляпунов. В общих чертах содержание формулировки Центральной предельной теоремы может быть высказано следующим образом.

Распределение суммы большого числа независимых случайных величин (не обязательно нормально распределенных) при весьма общих условиях близко к нормальному распределению.

Этим и определяется особая роль, нормально распределенных случайных величин, поскольку с суммами большого числа случайных слагаемых приходится часто иметь дело и в самой теории вероятностей и в ее приложениях.

Проиллюстрируем вышесказанное на следующем примере. Рассмотрим производство, на котором изготовляются большие партии однотипных изделий. Все наиболее существенные характеристики выпускаемых изделий должны соответствовать определенному стандарту. Однако в действительности наблюдаются отклонение от стандарта, которые порождаются причинами случайного характера (следует учесть, что выпуск изделий связан , как правило, со многими операциями, некоторые из которых не могут быть выполнены абсолютно точно). Каждая из этих причин сама по себе порождает ничтожную ошибку X , но, складываясь, такие ошибки, могут давать ощутимые отклонения от стандарта. Здесь, опираясь на Центральную предельную теорему, можно утверждать, что суммарное отклонение от стандарта представляет случайную величину, закон распределения которой близок к нормальному закону распределения.

Можно привести много подобных примеров из жизни. Они объясняют, почему нормальный закон так часто встречается в практических задачах.