3. Характеристики случайных величин.

Определение. Математическим ожиданием дискретной случайной величины X с законом распределения (2) называется величина

M[X] = p₁x₁ + p₂x₂ + ... + p₃x₃ + ... (4)

Замечание. Математическое ожидание представляет взвешенное среднее значение случайной величины с весовыми коэффициентами равными соответствующим вероятностям. Математическое ожидание часто также называют средним значением случайной величины.

В дальнейшем, наряду с обозначением (4), для математического ожидания M[X] будем использовать обозначение .

Заметим, что если X и Y случайные величины, то X ², Y ², CX, X + C, X – C ( где ) и X + Y также являются случайными величинами.

Перечислим основные свойства математического ожидания.

1⁰. M[C] = C, где С есть случайная величина, принимающая только постоянное значение С, то есть величина с законом распределения

X	C
P	1

2⁰. M[CX] = C M[X] ;

3⁰. M[X + Y] = M[X] + M[Y].

Определение. Дисперсией дискретной случайной величины X с законом распределения (2) называется величина

(5)

Величина называется среднеквадратическим отклонением случайной величиныX.

Заметим, что дисперсия характеризует величину отклонения (рассеивания) случайной величины X от ее среднего значения .

Если рассмотреть случайную величину , то очевидно, что

(7)

Утверждение. Если X дискретная случайная величина, то

(8)

Доказательство.

Из (7) и свойств 1⁰ – 3⁰ следует

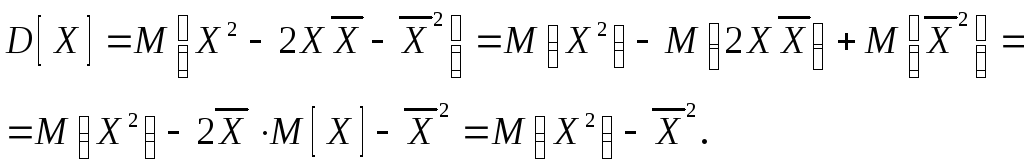
Утверждение доказано.

Сформулируем основные свойства дисперсии дискретной случайной величины:

1⁰. D[C] = 0;

2⁰. D[CX] = C² D[X];

3⁰. D[αX + β] = α² D[X].

4. Примеры дискретных случайных величин.

Приведем примеры часто встречающихся случайных величин.

1. Равномерно распределенная случайная величина.

Определение. Случайная величина X называется равномерно распределенной, если она принимает конечное число значений с одинаковой вероятностью, то есть закон распределения имеет вид.

X	x1	x2	...	xn
P	p	p	...	p

где pn = 1, то есть .

Задача. Доказать, что .

Пример. Бросается игральный кубик. Случайная величина X равна числу выпавших очков. Закон распределения X имеет вид

X	1	2	3	4	5	6
P

2. Биномиальное распределение.

Производится n независимых опытов. В каждом из них с одной и той же вероятностью p может наступить некоторое событие A. Случайная величина X равна числу наступлений события A в n опытах. Закон распределения случайной величины X имеет вид

X	0	1	2	...	k	...	n – 1	n
P	Pn(0)	Pn(1)	Pn(2)	...	Pn(k)	...	Pn(n – 1)	Pn(n)

где по формуле Бернулли

.

Задача. Доказать, что

3. Геометрическое распределение.

Рассмотрим схему Бернулли. Пусть иСлучайная величинаX равна количеству испытаний до первого наступления события .

Очевидно, что X может принимать любое значение Легко видеть, что случайная величинаX примет значение если наступит событиеТак как все испытания независимы, то

Поэтому закон распределения имеет вид

Задача. Доказать, что

4. Распределение Пуассона.

Определение. Говорят, что дискретная случайная величина распределена по закону Пуассона, если ее закон распределения имеет вид

Здесь λ > 0.

Задача. Доказать, что