6. Применение формул комбинаторики при решении задач по теории вероятности.

Пример 1. В записанном номере телефона оказались стёртыми две последние цифры, но абонент помнит, что они различные. Найти вероятность того, что набирая номер наугад, он попадёт к нужному лицу?

Решение.

Пространством элементарных событий в этой задаче будет множество ={(0,1),(0,2),…,(8,9)} всевозможных упорядоченных пар различных цифр. Число таких пар, очевидно, равно числу размещений без повторений из 10 по 2 , поскольку всего цифр n=10 штук, а k=2. Пусть  есть случайное событие, состоящее в том, что абонент набрал нужный номер. Очевидно, что  состоит из какой-то одной пары (m,n), где m и n различные цифры, то есть  есть элементарное событие. Следовательно =1. А поскольку по условию все исходы равновозможны, то из формулы (3), найдём . (Из 90 равновозможных исходов событию  благоприятствует только одно).

Пример 2. Найти вероятность того, что при случайном выборе четырёх букв из слова “история” будут получены буквы, из которых можно составить слово “сито”.

Первое решение.

Общее число равновозможных исходов (то есть различных выборов 4-х букв данного слова) равно числу сочетаний 4 букв из 7 букв, составляющих слово “история”, то есть

.

Так как буквы “с” “т” и “о” в слове “история” могут быть выбраны одним способом, а буква “и”  двумя способами, то число благоприятных исходов равно 1112=2. Следовательно, искомая вероятность .

Второе решение.

В этом примере пространство элементарных событий ={(т,я,и,и),(р,о,с,т),…} состоит из всевозможных четвёрок букв из слова “история” и порядок следования букв в четвёрках роли не играет. Поэтому =. Из этих четвёрок только две могут составить слово “сито”, поскольку буква “и” в слове “история” встречается два раза. Пусть  есть случайное событие, состоящее в получении слова “сито”. Тогда =2, поскольку ={(с,и,т,о), (с,и,т,о)} (буквы “и” разные).А так как все четвёрки равновероятны, то .

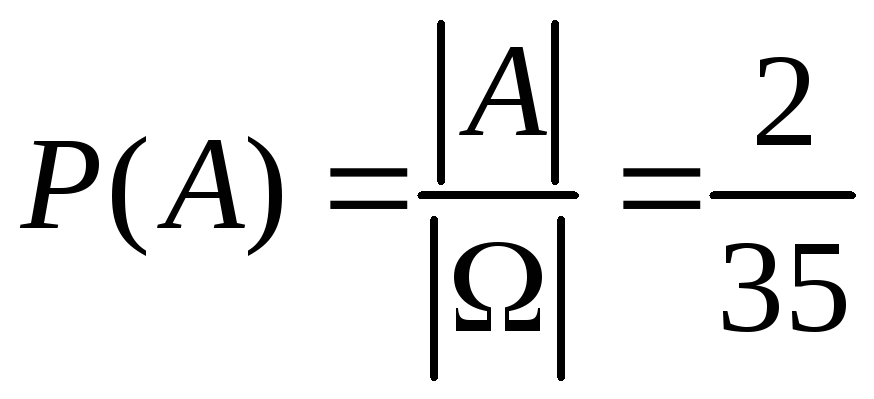Известно, что теория вероятностей родилась в XVII веке, когда такие учёные, как Б. Паскаль, П. Ферма и Х. Гюйгенс, впервые стали подсчитывать вероятность появления различных комбинаций в азартных играх, таких как игра в кости и в карты. Рассмотрим пример из игры в “покер”.

Пример 3. Игра в “покер”. В колоде 52 карты от 2 до туза, четырёх мастей. Каждому игроку сдаётся 5 карт. Найти вероятность того, что данный игрок получит “три  два”, то есть “три дамы и два туза”, или “три семёрки и два короля”, или “три двойки и две девятки” и т. д.

Решение.

Пять карт из 52 можно выбрать способами. Три карты из 4-х одинаковых (4 туза, 4 короля, и т. д.) можно выбратьспособами. Всего имеется 13 четвёрок. Поэтому различные тройки можно выбрать 413 способами. Если тройка выбрана, то осталось 12 четвёрок. В каждой четвёрке две карты можно выбрать способами. Поэтому различные двойки можно выбрать 612 способами. Таким образом, различные комбинации “32” можно получить 413612 различными способами. Поэтому искомая вероятность равна .