Тема 5: Числовые характеристики случайных дискретных величин: математическое ожидание, дисперсия, среднеквадратичное отклонение.

1. Математическое ожидание и дисперсия.

Определение. Пусть X непрерывная случайная величина, имеющая

плотность вероятности такую, что интегралы

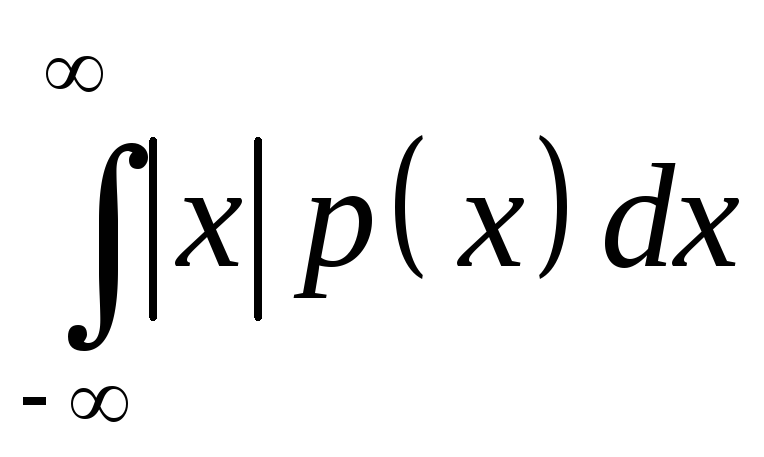и

сходятся.

Определение. Математическим ожиданием случайной величины X называется выражение

Определение. Дисперсией случайной величины X называется

Определение. Величина называется среднеквадратическим отклонением.

Теорема. Для справедливы следующие формулы:

и

Для математического ожидания и дисперсии непрерывной случайной величины справедливы свойства математического ожидания и дисперсии дискретной случайной величины.

Сформулируем еще одно свойство.

Теорема. Если X и Y независимые случайные величины, то

и

Математическое ожидание и дисперсия нормально распределенной величины определяются в следующей теореме.

Теорема. Если X есть нормально распределенная величина, распределенная по закону , то

Задача. Найти математическое ожидание и дисперсию равномерно распределенной случайной величины.

2. Нормированные случайные величины.

Определение. Случайная величина X называется нормированной, если и

Из любой случайной величины с помощью линейного преобразования можно получить нормированную.

Теорема. Если X произвольная случайная величина и , то случайная величина- нормированная.

Доказательство.

Воспользовавшись свойствами математического ожидания и дисперсии, получим

Теорема доказана.

Тема 9: Статистические методы обработки экспериментальных данных. Выборка, генеральная совокупность. Относительные частоты. Гистограмма. Статистическая средняя и дисперсия. Статистическое оценивание и проверка гипотез. Случайные процессы.

1.Определение характеристик случайных величин на основе опытных данных.

Предположим, что изучается некоторая случайная величина X. С этой целью производится ряд независимых испытаний, в каждом из которых величина X принимает то или иное значение. Совокупность полученных значений x₁, x₂, ..., x_n величины X, где n – число испытаний, называют выборкой или статистическим рядом. Этот ряд играет роль числового материала, подлежащего дальнейшей обработке и анализу. Разработкой методов, позволяющих по результатам обследования выборки делать обоснованные заключения о характере случайной величины X, занимается математическая статистика. Эта наука возникла в 17 веке и развивалась параллельно с теорией вероятностей. На практике методы математической статистики используются в тех случаях, когда требуется изучить распределение большой совокупности предметов по некоторому признаку, например, распределение множества людей по возрасту и т.д. Так как практически любой признак допускает количественную оценку, то, вместо того чтобы говорить о распределении предметов по признаку, можно говорить о распределении некоторой случайной величины. С этой точки зрения, испытание, с которым связана случайная величина, заключается в выборе наугад одного представителя данной совокупности, а значение, принимаемое случайной величиной, есть значение признака для этого представителя. Введем следующее определение.

Определение 1. Выборочной совокупностью (выборкой или статистическим рядом) называется совокупность случайно отобранных объектов. Генеральной совокупностью называется совокупность всех объектов, из которых производится выборка. Объемом совокупности (выборочной или генеральной) называется число всех объектов этой совокупности.

Пусть из генеральной совокупности извлечена выборка объемом n. Расположим результаты выборки в таблице.

i (номер испытания)	1	2	...	n
значение λi случайной величины X в i-м испытании	λ1	λ2	...	λn

Среди приведенных значений случайной величины X могут быть и равные. Объединив равные значения случайной величины X, получим следующую таблицу:

значение xi случайной величины X	x1	x2	...	xk
число xi появлений значения xi	n1	n2	...	nk

где k – число различных возможных значений величины X.

Определение 2. Наблюдаемые в выборке значения x₁, x₂, ..., x_k случайной величины X называют вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом.

Числа n₁, n₂, ..., n_k называют частотами соответствующих значений случайной величины X. Отношение частоты n_i к объему выборки n называется относительной частотой значения x_i и обозначается через w_i, т. е.

, .

Очевидно, что сумма частот всех значений случайной величины равна объему выборки, т.е. n₁ + n₂ + ... + n_k = n. Отметим также, что

,

т.е. сумма относительных частот всех значений случайной величины X равна единице.

Определение 3. Статистическим распределением случайной величины X называют перечень вариант и соответствующих им частот или относительных частот.

Как правило, статистическое распределение записывают в виде таблицы (1):

X	x1	x2	...	xk
w	w1	w2	...	wk

Если X – непрерывная случайная величина, то ее статистическое распределение целесообразно представить в виде:

X	(c1,c2)	[c2,c3)	...	[cs-1,cs)
W	w1	w2	...	wk

где (c_s-1,c_s) (или [c_s-1,c_s)) – промежуток, которому принадлежат все возможные значения случайной величины X, а w_i – относительная частота попаданий случайной величины X в данный промежуток.

Для наглядности статистическое распределение дискретной случайной величины иллюстрируется полигоном распределения: точки с координатами (x₁, w₁), (x₂, w₂), ... , (x_k, w_k) изображают на координатной плоскости и соединяют их прямолинейными отрезками:

Для иллюстрации распределения непрерывной случайной величины используются гистограммы – ступенчатые фигуры, состоящие из прямоугольников, основаниями которых служат интервалы (c_i,c_i+1), , а площади прямоугольников равны соответственноw_i, :

Гистограмма представляет собой приближение графика плотности распределения непрерывной случайной величины.

Рассмотрим числовые характеристики дискретной случайной величины, заданной статистическим распределением.

Определение 4. Средним значением случайной величины X, заданной статистическим распределением (1), называют число , равное

(2)

Число определяет среднее значениеX для выборки. Если в качестве выборки рассматривать всю генеральную совокупность (объема N), то число будет представлять собой вероятность, с которой случайная величинаX принимает значение ,, и равенство (2) можно записать в виде

.

Это означает, что для выборочной совокупности достаточно большого объема справедливо .

Определение 5. Статистической дисперсией случайной величины X, заданной статистически распределением (1), называется число

(3)

Из равенства (3) следует, что число является средним значением случайной величины. Поэтому при большом объеме выборки имеет место приближенное равенство.

Определение 6. Число называютсредним квадратическим отклонением случайной величины X, заданной статистическим распределением (1).

36