§2. Понятие функции нескольких переменных

Определение. Пусть G – некоторое множество в . Отображение называетсядействительной функцией n действительных переменных.

Обозначается .

Множество G называется областью определения функции, а множество значений, которые принимает u – множеством значений функции f.

Вслучаеn=2 обычно пишут z=f(x,y), а при n=3 u=f(x,y,z).

Пример. Найти область определения функции .

 D(z):

. 

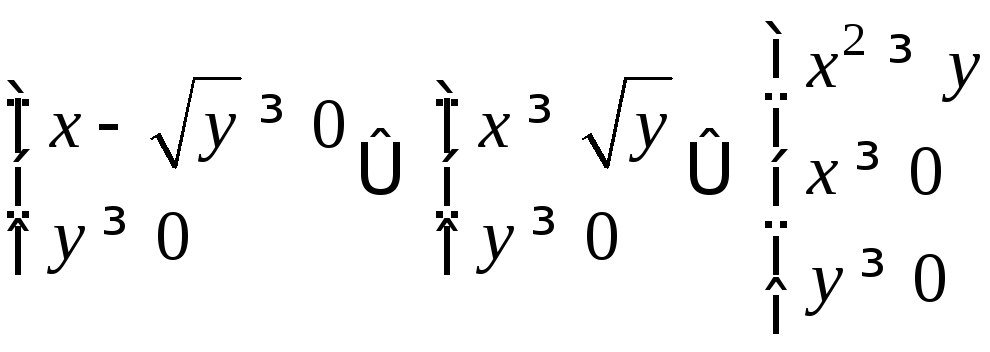
Пусть дана функция двух переменных z=f(x,y) с областью определения . Функцияf задается множеством точек . Значит, это множество можно изобразить в трехмерном координатном пространстве. Получим множество точек, которое называется графиком функции z=f(x,y). Часто (но не обязательно) графиком такой функции является поверхность. Не каждая поверхность может быть графиком функции двух переменных. Если поверхность является графиком функции двух переменных, то любая прямая, параллельная оси Оz пересекает ее не более, чем в одной точке.

П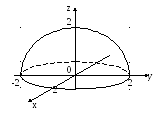ример.  Рассмотрим функцию

.

- круг с центром в (0;0), радиусом R=2.

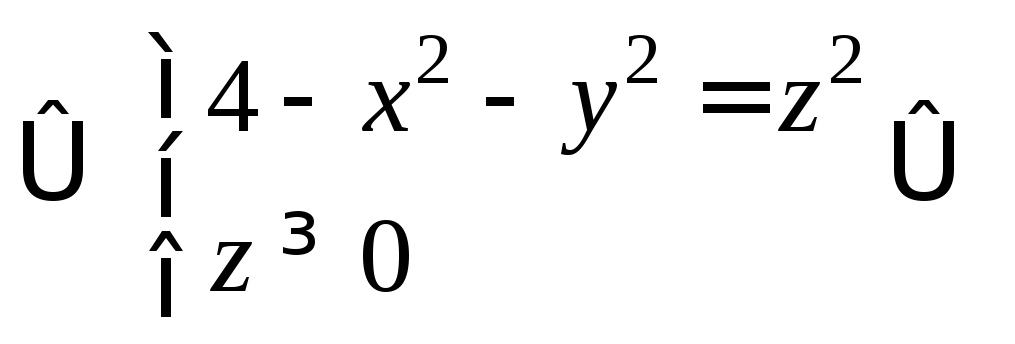
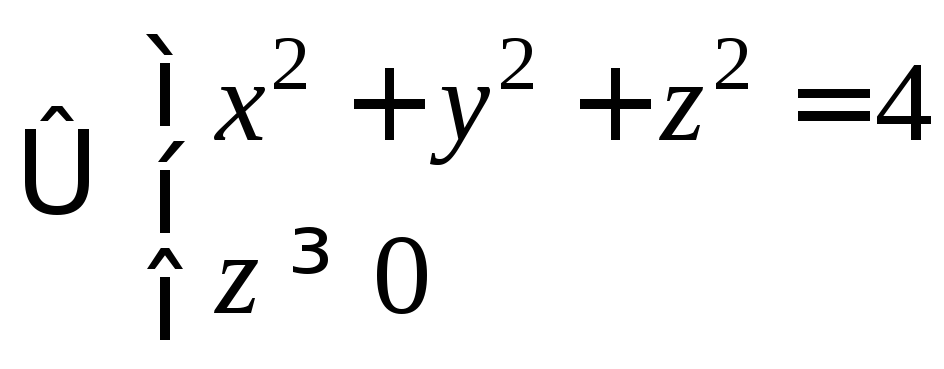- верхняя полусфера с центром в (0;0;0), радиусом R=2. 

Пусть функция z=f(x,y) задана на . Пересечем график функции плоскостьюz=a. В сечении получим линию

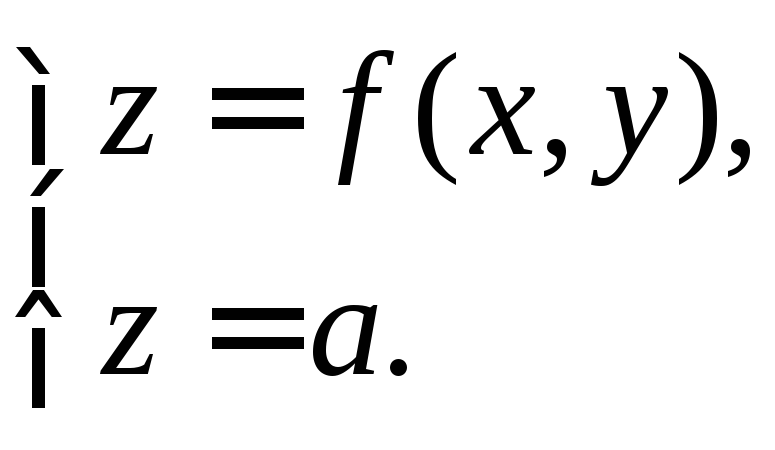
Спроектируем ортогонально эту линию на плоскость хОу. Линия f(x,y)=a лежит в D и называется линией уровня функции f.

Определение. Линией уровня функции z=f(x,y) называется множество точек (x,y) из области определения функции, в которых функция принимает одно и то же значение а.

Придавая а разные значения, будем получать различные линии уровня. Значит, если а – параметр, то f(x,y)=a – семейство линий уровня. Обычно в качестве а берут числа а₁,а₂,а₃,…, образующие арифметическую прогрессию. В этом случае линии уровня дают некоторое наглядное представление о графике функции z=f(x,y). В тех местах, где линии уровня сгущены, функция возрастает быстрее, чем в тех местах, где они разрежены.

Аналогично вводится понятие поверхностей уровня функции трех переменных u=f(x,y,z): . Еслиа – параметр, то f(x,y,z)=а – семейство поверхностей уровня.

§3. Предел и непрерывность функции двух переменных

Лк (2ч)

1. Понятие предела функции двух переменных

Пусть функция z=f(x,y) определена на множестве . ПустьМ₀(х₀,у₀) – предельная точка множества G.

Определение 1 (по Коши). Число А называется пределом функции f(x,y) в точке М₀(х₀,у₀), если >0 =()>0: M(x,y)G: 0<(M₀,M)< выполнено неравенство | f(x,y)-A|<.

Обозначается или.

Напомним, что в .

Определение 2 (по Гейне). Число А называется пределом функции f(x,y) в точке М₀(х₀,у₀), если для произвольной последовательности точек {M_n(x_n,y_n)}, M_nG, M_n M₀ n, таких чтовыполнено.

Равносильность этих определений доказывается аналогично случаю функции одной действительной переменной.

Аналогично вводится понятие предела функции n действительных переменных.

Для предела функции n переменных справедливы все свойства предела функции одной переменной.

Пример 1. Вычислить .

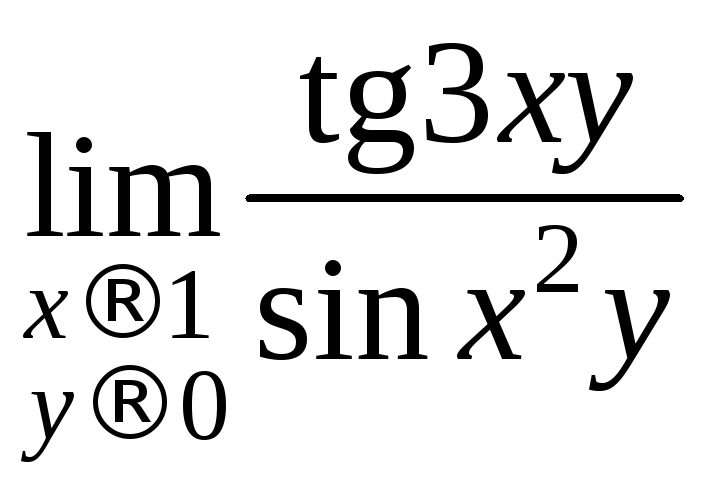 Т. к. функции 3ху и х²у являются бесконечно малыми при х1, у0, то tg3xy3xy, sinx²yx²y. Тогда

.

Пример 2. Доказать, что функция 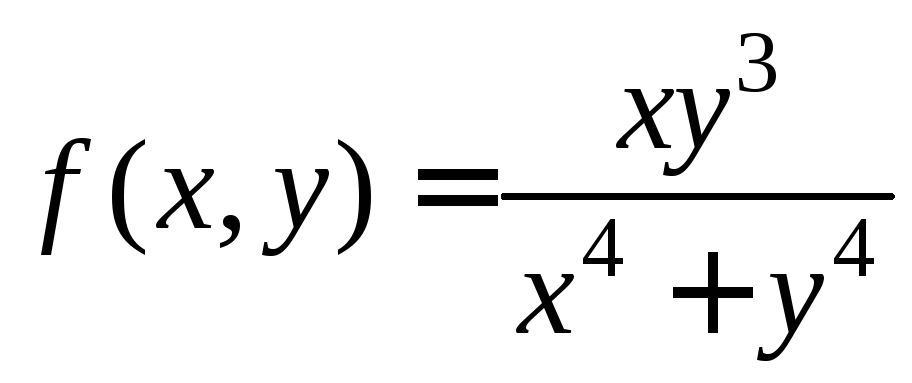не имеет предела в точке О(0;0).

 . Т.о., (0;0) – предельная точка D(f ). Покажем, что не существует.

1 способ. Пусть М(х;у)О(0;0) по прямой у=kx, проходящей через точку О. Тогда

.

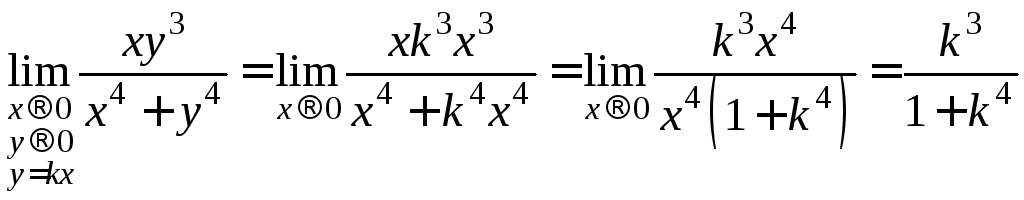Т.о., приближаясь к точке О(0;0) по различным прямым, соответствующим различным значениям k, получаем, что функция стремится к различным значениям. Например, при k=0, т.е. приближаясь к точке О(0;0) по оси Ох =0; приk=1, т.е. приближаясь к О(0;0) по прямой у=х 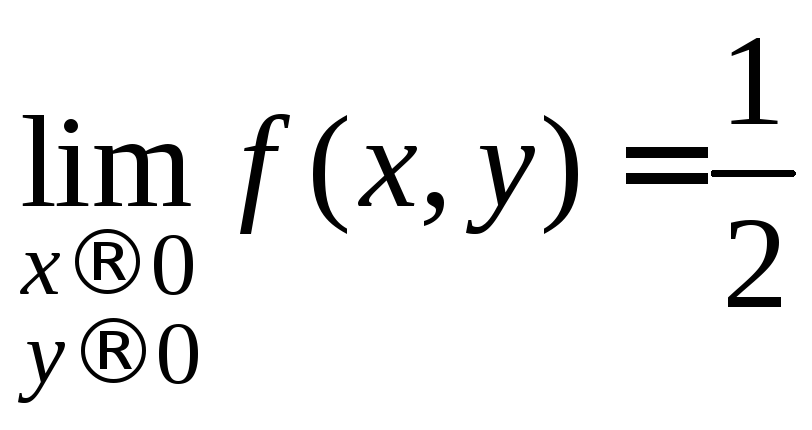и т.д. Следовательно,не существует.

2 способ. Рассмотрим две различные последовательности точек, стремящиеся к О(0;0).

Первая последовательность 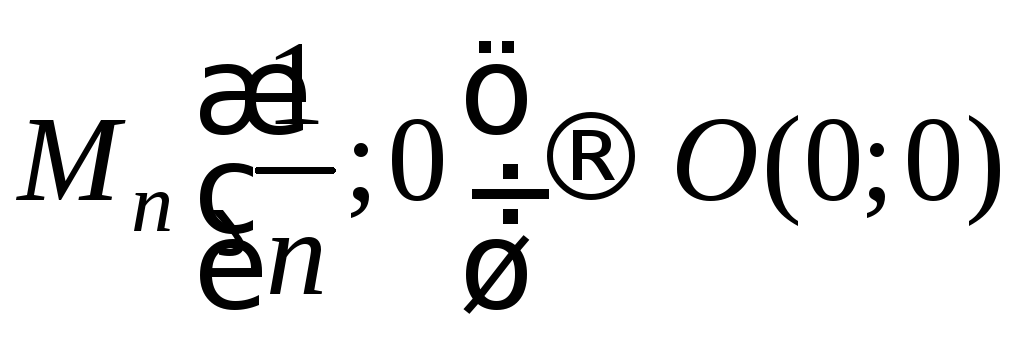по положительной части оси Ох. Тогда .

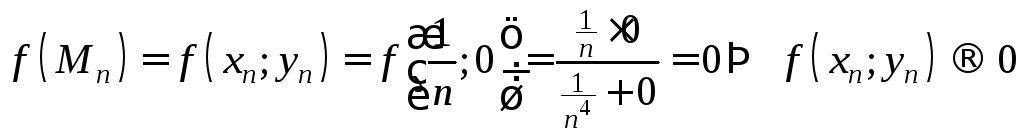Вторая последовательность по направлению биссектрисы первого координатного угла (по прямойу=х). Тогда

.

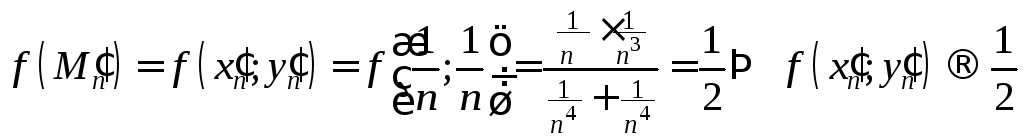Т.о., двум различным последовательностям точек, стремящимся к О(0;0) по разным направлениям, соответствуют две последовательности значений функции, имеющие разные пределы. Согласно определению предела функции по Гейне это означает, что функция не имеет предела в точке (0;0).

Пример 3. Найти .

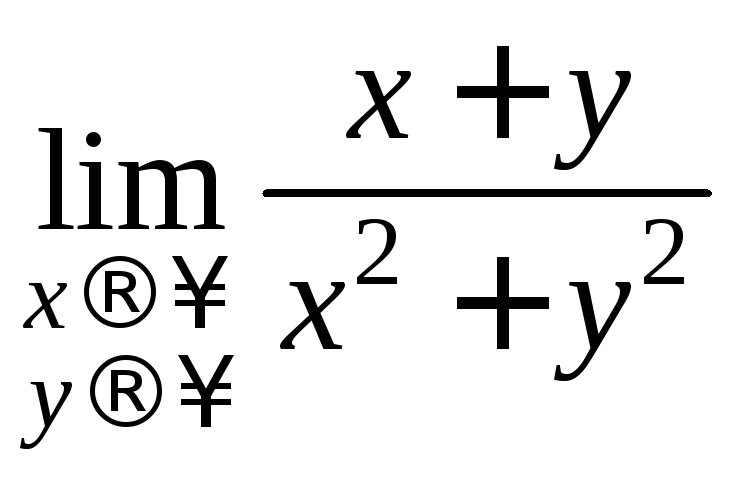 Перейдем к полярным координатам с центром в точке О(0;0):

,

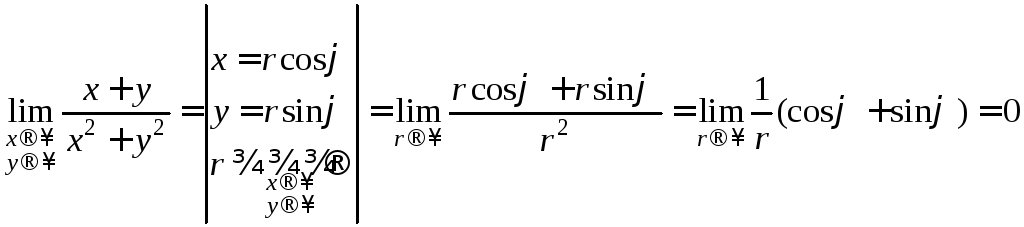т.к. функция - бесконечно малая при r, а функция (cos +sin) ограничена.