
- •1.Форматы ( гост 2301-68)
- •1.Сопряжения
- •2.Построение уклонов и конусностей.
- •1. Виды.
- •2. Разрезы.
- •3. Правила применяемые при соединении части вида с частью разреза.
- •4. Сечения.
- •1.Виды аксонометрических проекций.
- •2,3,4.Прямоугольная изометрия, Прямоугольная диметрия.
- •1. Метод проекций
- •2.Комплексный чертеж точки
- •3.Комплексный чертеж прямой.
- •4.Деление отрезка в заданном отношении.
- •5.Способы задания плоскости
- •6. Положение прямой относительно плоскостей проекций.(прямые …)
- •7. Положение плоскости относительно плоскости проекций.
- •8. Главные линии плоскости.
- •9.Свойства принадлежности.
- •10.Определение натуральной величины прямой общего положения( 2 способа)
- •11. Определение угла наклона прямой к плоскости проекции.
- •14. Определение точки встречи прямой и плоскости.
- •15. Взаимное положение плоскостей.
- •16. Определение линии пересечения двух плоскостей.
- •17. Метод замены плоскостей проекций.
- •18. Понятие многогранника.
- •19. Поверхности.
- •20-22. Пересечение многогранником плоскостью.
- •23) Метод сфер
- •22)Способ секущих плоскостей
- •9.4.2.Пересечение проецирующего тела вращения с непроецирующим
10.Определение натуральной величины прямой общего положения( 2 способа)
|
Определение длины отрезка прямой линиии углов наклона прямой к плоскостям проекций. |
Длину отрезка АВ можно определить из прямоугольного треугольника АВС |AС|=|A1B1|, |BС|= , угол угол наклона отрезка к плоскости П1, угол наклона отрезка к плоскости П2. Для этого на эпюре (рис.3.17) из точки B1 под углом 900 проводим отрезок 1*, полученный в результате построений отрезок A1B1*и будет натуральной величиной отрезка АВ, а угол B1A1B1* =α. Рассмотренный метод называется методом прямоугольного треугольника.
Однако все построения можно объяснить, как вращение треугольника АВСвокруг стороны AС до тех пор, пока он не станет параллелен плоскости П1, в этом случае треугольник проецируется на плоскость проекций без искажения. Подробнее вращение вокруг оси параллельной плоскости проекций рассмотрены в разделе «Методы преобразования ортогональных проекций»
|
|
|
|
а) модель |
б) эпюр |
Метод замены плоскостей
зменение взаимного положения изучаемого объекта и плоскостей проекций достигается путем замены одной из плоскостей П1 или П2 новой плоскостями П4 (рис. 148). Новая плоскость всегда выбирается перпендикулярно оставшейся плоскости проекций.
Для решения некоторых задач может потребоваться двойная замены плоскостей проекций (рис. 149). Последовательный переход от одной системы плоскостей проекций к другой необходимо осуществлять, выполняя следующее правило: расстояние от новой проекции точки до новой оси должно равняться расстоянию от заменяемой проекции точки до заменяемой оси.
Задача 1: Определить натуральную величину отрезка АВ прямой общего положений (рис. 148). Из свойства параллельного проецирования известно, что отрезок проецируется на плоскость в натуральную величину, если он параллелен этой плоскости.
Выберем новую плоскость проекций П4, параллельно отрезку АВ и перпендикулярно плоскости П1. Введением новой плоскости, переходим из системы плоскостей П1П2 в систему П1П4 , причем в новой системе плоскостей проекция отрезка А4 В4 будет натуральной величиной отрезка АВ.
|
|
|
|
| |
|
| ||||
|
| ||||
|
| ||||
|
а) модель |
б) эпюр | |||
|
Рисунок 148. Определение натуральной величины отрезка прямой методом замены плоскостей проекций | ||||
Задача 2: Определить расстояние от точки А до прямой общего положения, заданной отрезком ВС (рис._149).
|
|
|
|
|
|
11. Определение угла наклона прямой к плоскости проекции.
Длину отрезка АВ и - угол наклона отрезка к плоскости П1 можно определить из прямоугольного треугольника АВС |AС|=|A1B1|, |BС|=Z. Для этого на эпюре (рис.31) из точки B1 под углом 900 проводим отрезок |B1B1*|=Z, полученный в результате построений отрезок A1B1* и будет натуральной величиной отрезкаАВ, а угол B1A1B1*=. Рассмотренный метод называется методом прямоугольного треугольника. Тот же результат можно получить при вращении треугольника АВС вокруг стороны AС до тех пор, пока он не станет параллелен плоскости П1, в этом случае треугольник проецируется на плоскость проекций без искажения. Подробнее вращение вокруг оси параллельной плоскости проекций рассмотрены в разделе «Методы преобразования ортогональных проекций».
|
|
|
|
|
|
| |||
|
| |||
|
а)
модель
б)эпюр |
| ||
|
Рисунок 31. Определение натуральной величины отрезка и угла его наклона к горизонтальной плоскости проекций | |||
Длину отрезка АВ и -угол наклона отрезка к плоскости П2 можно определить из прямоугольного треугольникаАВС |AС|=|A2B2|, |BС|=Y. Построения аналогичные рассмотренным, только в треугольнике АВВ* сторона|BВ*|= и треугольник совмещается с плоскостью П2 (рис.32).
|
|
|
|
| |||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||
|
а) модель б) эпюр Рисунок 32. Определение натуральной величины отрезка и угла его к фронтальной плоскости.
12. Определение расстояния от точки до прямой. ОПРЕДЕЛЕНИЕ РАССТОЯНИЯ ОТ ТОЧКИ ДО ПРЯМОЙ ОБЩЕГО ПОЛОЖЕНИЯ Для того чтобы определить расстояние от точки до прямой, необходимо из точки опустить на прямую перпендикуляр. Прямого решения эта задача не имеет, так как прямой угол между прямыми общего положения будет проецироваться с искажением. Проведем
через точку М плоскость ,
перпендикулярную прямой 1 (рис.10.4).
Зададим эту плоскость двумя
пересекающимися прямыми - горизонталью
и фронталью. В этом случае горизонтальная
проекция горизонтали будет
перпендикулярна горизонтальной
проекции прямой1.
Фронтальная проекция фронтали -
перпендикулярна фронтальной проекции
прямой 1. Построим точку встречи прямой 1 с плоскостью , l = К. Так как прямая 1 перпендикулярна плоскости , следовательно, она перпендикулярна любой прямой, принадлежащей плоскости , в том числе - и прямой МК, т.е. прямая МК перпендикулярна прямой 1. Отрезок МК спроецировался с искажением. Его натуральную величину найдем способом вращения вокруг фронтально проецирующей прямой, проходящей через точку М. M1K1 = MK . Решение задачи методом проецирования на дополнительнуюплокость приведено на рис.10.5 в следующем разделе. M5K5 = MK .
13.Взаимное положение прямой и плоскости.
При решении вопроса о параллельности прямой линии и плоскости необходимо опираться на известное положение стереометрии:прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в этой плоскостии не принадлежит этой плоскости. Задача. Дано: проекции плоскости общего положения ABC и прямой общего положения а. Требуется оценить их взаимное положение (рис.5.20).Гайки навинчиваются на резьбовой конец болта, при этом соединяемые детали зажимаются между гайкой и головкой болта. Рисунок плоскостями гипсовой головы в двух поворотах Это задание отчасти напоминает предыдущее, но теперь мы пользуемся плоскостями произвольной формы и ориентации. Суть задания заключается в том чтобы выразить конкретную форму через минимальное количество плоскостей но с максимальным сходством. Пропуск или ошибка хотя бы в одном из размеров делают чертеж непригодным к использованию. Последовательность нанесения размеров
Для этого через прямую а проведем вспомогательную секущую плоскость - в данном случае горизонтально проецирующая плоскость. Найдем линию пересечения плоскостей и АВС- прямую п (DF). Проекция прямой п на горизонтальную плоскость проекций совпадает с проекцией а1 и со следом плоскости . Проекция прямой п2 параллельна а2, п3 параллельна а3, следовательно, прямая а параллельна плоскости AВС.
Нахождение точки пересечения прямой линии и плоскости – основная задача начертательной геометрии. Задача. Дано: плоскость AВС и прямая а. Требуется найти точку пересечения прямой с плоскостью и определить видимость прямой по отношению к плоскости. Для решения задачи: Через горизонтальную проекцию прямой а1 проведем вспомогательную горизонтально проецирующую плоскость (таким образом а). Горизонтальный след плоскости 1 пересекает проекцию плоскости A1В1С1 в точках D1 и F1, которые определяют положение горизонтальной проекции п1- линии пересечения плоскостей и AВС. Для нахождения фронтальной и профильной проекции пспроецируем точки D и F на фронтальную и профильную плоскости проекций. На фронтальной и профильной проекциях линия пересечения плоскостей п пересекает проекции а в точке К, которая и является проекцией точки пересечения прямой а с плоскостью AВС, по линии связи находим горизонтальную проекцию К1. Методом конкурирующих точек определяем видимость прямой а по отношению к плоскости AВС.
Таким образом алгоритм решения задачи состоит из следующей последовательности действий (рис.5.21): 1. Построение вспомогательной секущей плоскости ( горизонтально – проецирующая плоскость ), которую проводят через прямую аа; 2. Построение линии пересечения вспомогательной плоскости и заданной плоскости п; 3. Определение искомой точки К, как точки пересечения двух прямых, заданной - а и полученной в результате пересечения плоскостей – п Ка п. В качестве вспомогательной плоскости рекомендуется брать одну из проецирующих плоскостей. 4. Определение видимости прямой а относительно плоскости
Докажем следующую теорему о перпендикуляре к плоскости: Если прямая перпендикулярна плоскости, то горизонтальная проекция этой прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция – фронтальной проекции фронтали плоскости. Пусть прямая n, перпендикулярная плоскости, пересекает плоскость BCD в точке N, тогда по условию n перпендикулярна любой прямой плоскости. Проведем в плоскости BCD горизонталь h, а на основании теоремы о проецировании прямого угла можно утверждать, что на горизонтальную плоскость проекций они проецируются под прямым углом, т.е. n1 h1. Аналогично для фронтали – f n f2 n2. Справедлива и обратная теорема: Если проекции прямой перпендикулярны одноименным проекциям соответствующих главных линий плоскости (горизонтали и фронтали), то такая прямая перпендикулярна плоскости. Доказательство следует из теоремы о проецировании прямого угла. Исходя из рассмотренных теорем, можно решить задачу о построении перпендикуляра к плоскости из точки А (рис.5.22). Задача. Дано: плоскость ВСD и точка А. Требуется построить прямую линию n проходящую через точку А и перпендикулярную плоскости ВСD. В плоскости ВСD построим фронталь f и горизонталь h. В горизонтальной плоскости проекций проведем через точку А1 прямую n1перпендикулярно горизонтальной проекции горизонтали h1, а на фронтальной плоскости проекций через точку А2 прямую n2перпендикулярно фронтальной проекции фронтали f2, согласно выше сказанному полученная прямая n будет перпендикулярна плоскостиВСD.
| ||||||||||||||||||||||||||||||||||||

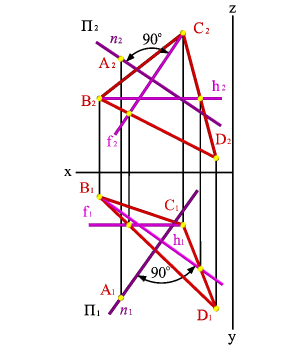
а) модель б) эпюр
Рисунок 5.22. Построение прямой, перпендикулярной плоскости



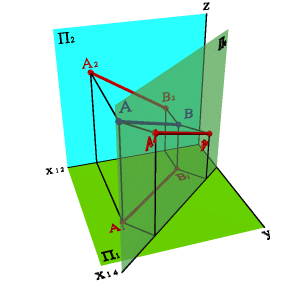







 Рис. 10.4.
Рис. 10.4.


