3.Комплексный чертеж прямой.

Учитывая то, что прямую линию в пространстве можно определить положением двух ее точек, для построения ее на чертеже достаточно выполнить комплексный чертеж этих двух точек, а затем соединить одноименные проекции точек прямыми линиями. При этом получаем соответственно горизонтальную и фронтальную проекции прямой.

Профильную проекцию прямой можно построить с помощью профильных проекций точек А и В. Кроме того, профильную проекцию прямой можно построить, используя разность расстояний двух ее точек до фронтальной плоскости проекций, т. е. разность глубин точек (рис. 69, в). В этом случае отпадает необходимость наносить оси проекций на чертеж. Этот способ, как более точный, и используется в практике выполнения технических чертежей.

4.Деление отрезка в заданном отношении.

В пространстве точка и прямая относительно друг друга могут занимать два положения: точка лежит на прямой и точка не лежит на прямой.

Если точка С лежит на прямой АВ, то, на основании свойства проекций при параллельном проецировании, её проекции лежат на одноимённых проекциях этой прямой и на одной линии связи.

При рассмотрении свойств параллельного проецирования установлено, что отношение отрезков прямой равно отношению их проекций. Для того чтобы разделить отрезок прямой в заданном отношении, достаточно разделить в том же отношении проекции отрезка.

Пусть требуется отрезок АВ разделить точкой С в заданном отношении АС :СВ = 2:1. Обратимся к ортогональному чертежу отрезка АВ.

Например, из первой проекции В1 точки В проведём вспомогательную прямую под произвольным углом. На этой прямой отложим 3 равных отрезка любой длины. Соединим точку А1 и точку 3. Через точку 1 проведём прямую || А13. При пересечении этой прямой с отрезком А1В1 получим искомую точку С1, которая делит первую проекцию отрезка АВ в заданном отношении: А1С1 : С1В1 = 2:1. Так как по свойству проекций точки С1 и С2 должны лежать на одной линии связи, то теперь для того чтобы найти вторую проекцию С2точки С достаточно провести линию связи и найти точку её пересечения с отрезком А2В2. Отметим точку С2, которая удовлетворяет условию А2С2 : С2В2 = 2:1.

Итак, мы построили на ортогональном чертеже отрезок АВ и отметили точку С, которая делит отрезокАВ в заданном отношении АС :СВ = 2:1.

5.Способы задания плоскости

1)Тремя точкми не лежащими на одной прямой

2)Прямой и точкой

3)Двумя пересекающимися прямыми

4)Двумя параллельными прямыми

5)Любой плоской фигурой

6)Следом(прямой по которой заданная плоскость пересекается с плоскостью проекции)

6. Положение прямой относительно плоскостей проекций.(прямые …)

Положение прямой относительно плоскостей проекций. Следы прямой.

В зависимости от положения прямой по отношению к плоскостям проекций она может занимать как общее, так и частные положения.

1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения (рис.3.4). Графические обозначения материалов в сечениях В машиностроении используются детали, изготовленные из различного материала. Для наглядности и выразительности чертежей введены условные графические обозначения материалов. ГОСТ 2.306—68 устанавливает графические обозначения материалов в сечениях и на фасадах, а также правила нанесения их на чертежи всех отраслей промышленности и строительства. Живопись маслом Мастерская живописи и рисунка История искусства Многогранники как поверхности и многогранники как тела Задание многогранников Геометрическими элементами многогранников являются вершины, ребра, грани и для многогранников-тел - пространство внутри многогранника. Все элементы можно представить в виде структурированного массива точек.

Италия в эпоху возрождения Культура христианской эпохи

а) модель Выполнение графических работ Многогранники Начертательная геометрия		б) эпюр
Рисунок 3.4. Прямая общего положения

2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:

2.1. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями (рис.3.5). Для любой пары точек горизонтали должно быть справедливо равенство

z_A=z_B   A₂B₂//0x; A₃B₃//0y   x_A–x_B#0, y_A–y_B#0, z_A–z_B=0.

а) модель		б) эпюр
Рисунок 3.5. Горизонтальная прямая

2.2. Прямые параллельные фронтальной плоскости  проекций называются фронтальными илифронталями(рис.3.6).

 y_A=y_B₁B₁//0x, A₃B₃//0z   x_A–x_B#0, y_A–y_B=0, z_A–z_B#0.

а) модель		б) эпюр
Рисунок 3.6. Фронтальная прямая

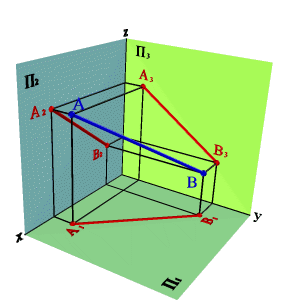
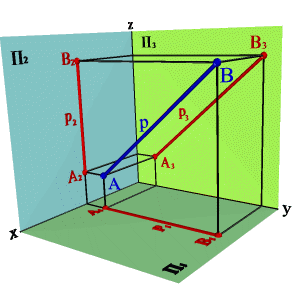
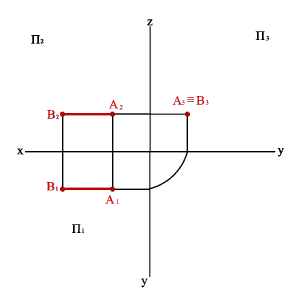
2.3. Прямые параллельные профильной плоскости проекций называются профильными (рис. 3.7).

x_A=x_B__y, A₂B₂//0z   x_A–x_B=0, y_A–y_B#0, z_A–z_B#0.

Различают восходящую и нисходящую профильные прямые. Первая по мере удаления от зрителя поднимается, вторая - понижается.

а) модель		б) эпюр
Рисунок 3.7. Профильная прямая

3. Прямые перпендикулярные плоскостям проекций, называются проецирующими. Прямая перпендикулярная одной плоскости проекций, параллельна двум другим.  В зависимости от того, какой плоскости проекций перпендикулярна исследуемая прямая, различают:

3.1. Фронтально проецирующая прямая - АВ (рис. 3.8)

x_A–x_B=0

y_A–y_B#0

z_A–z_B0,

а) модель		б) эпюр
Рисунок 3.8. Фронтально проецирующая прямая

3.2. Профильнопроецирующая прямая - АВ (рис.3.9)

x_А–x_B#0

y_А–y_B=0

 z_А–z_B=0,

а) модель		б) эпюр
Рисунок 3.9. Профильно-проецирующая прямая

3.3. Горизонтально проецирующая прямая - АВ (рис.3.10)

x_А–x_В=0

y_А–y_В=0

z_А–z_В#0.

а) модель		б) эпюр
Рисунок 3.10. Горизонтально-проецирующая прямая

4. Прямые параллельные биссекторным плоскостям (рис. 3.11)

АВ бис    x_A–x_B=0; z_B–z_A=y_B–y_A; СD//2бис    x_С–x_D=0; z_D–z_C=y_C–y_D.

Биссекторной плоскостью называется плоскость проходящая через ось 0х и делящая двухгранный угол между плоскостями проекций П₁и П₂ пополам. Биссекторная плоскость проходящая через 1 и 3 четверти называется первой биссекторной плоскостью (бис) ,а через 2 и 4 четверти - второй (бис).

5. Прямые перпендикулярные биссекторным плоскостям (рис. 3.11)

АВ2бис   x_A–x_B=0; z_B–z_A=y_В–y_А;_. СD1бис   x_С–x_D=0;z_D–z_C=y_C–y_D

а) модель		б) эпюр