1. Метод проекций

ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ

Основными видами проецирования являются центральное и параллельное. Центральное проецирование представляет собой общий случай проецирования геометрических образов из некоторого центра на плоскость.

Пусть задана плоскость П₁ и кривая линия k с точками А, В, С (рис.1.1).

 Рис.1.1

Возьмем некоторую точку S, не лежащую в плоскости П₁. Через точку S и точки А, В, С кривой k проведем прямые до пересечения с плоскостью П₁ в точках A₁, B₁, C₁. Проведя таким образом через S и каждую точку кривой k прямые, получим в плоскости П₁ изображение k₁кривой k.

В соответствии с описанным построением введем следующие понятия:

S - центр проекций; П₁ - плоскость проекций; кривая k с точками А, В, С - объект проецирования; SА, SВ, SС - проецирующие лучи;A₁,B₁,C₁ - центральные проекции точек А, В, С; k₁ - центральная проекция кривой k. Рассматривая каждую пространственную фигуру как совокупность точек, можно сказать, что проекция фигуры представляет собой множество проекций ее точек.

Свойства центрального проецирования:

1. Любая точка (кроме S) проецируется на плоскость проекций в единственную точку (рис.1).

2. Каждой точке (A, B, C, D,...), принадлежащей какой-либо линии (кривой или прямой), соответствует проекция (A₁, B₁, C₁, D₁, ...) этой точки на проекции данной линии (рис.1).

3. Кривая в общем случае проецируется в кривую, а прямая - в прямую. Если прямая совпадает с проецирующим лучом, например DE (рис.1), то она проецируется в точку D₁ E₁. Плоскость, проходящая через центр проекций, проецируется в прямую и называется проецирующей. Кривая, все точки которой принадлежат проецирующей плоскости, проецируется в прямую.

4. Точка пересечения линий проецируется в точку пересечения проекций этих линий (рис.1).

Центральное проецирование обладает большой наглядностью и применяется в строительном черчении, в архитектуре, в живописи и т.п. Недостатком центрального проецирования является сложность построения изображения предмета и определения истинных размеров. Поэтому оно имеет ограниченное применение в техническом черчении.

ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ

Параллельное проецирование можно рассматривать как частный случай центрального проецирования с бесконечно удаленным центром проекций. Осуществляется оно пучком параллельных проецирующих лучей заданного направления. Пусть требуется построить параллельную проекцию кривой k на плоскость П₁(рис.1.2).

 Рис. 1.2 Рис.1.3

Спроецируем в направлении s все точки кривой k на плоскость П₁. Чтобы спроецировать точки указанной кривой, например А, В, С, нужно провести через них прямые, параллельные направлению s, до пересечения с плоскостью П₁. Точки пересечения A₁,B₁,C₁ проецирующих лучей с плоскостью П₁ и будут параллельными проекциями точек А, В и С. Таким образом можно построить проекции множества точек кривой k. В зависимости от направления проецирования по отношению к плоскости проекций П₁ различают два вида параллельных проекций: косоугольную, когда проецирующие лучи не перпендикулярны к плоскости П₁ (рис. 1.2, кривая k), и прямоугольную (или ортогональную), когда проецирующие лучи перпендикулярны к плоскости проекций (рис.1.2, прямая а). Несмотря на то, что параллельное проецирование по сравнению с центральным дает меньшую наглядность, параллельные проекции, особенно ортогональные, обладают удобоизмеримостью и простотой построения. Поэтому ортогональное проецирование широко распространено в технике и является основным методом начертательной геометрии.

Свойства параллельного проецирования

При параллельном проецировании сохраняются все свойства центрального проецирования, а также возникают следующие новые свойства.

1. Проекции параллельных прямых параллельны между собой, т.е., если а b, то a₁ b₁. Пусть отрезки АВ и DE параллельны (рис. 1.3), тогда проецирующие плоскости AA₁BB₁ и DD₁E₁E будут также параллельны. Следовательно, линии A₁B₁ и D₁E₁ пересечения этих плоскостей с П₁ будут параллельны.

2.Отношение отрезков, принадлежащих параллельным прямым или одной прямой, равно отношению проекций этих отрезков, т.е., если ABDE, то AB / DE =  A₁B₁ / D₁E₁

3. При параллельном перемещении плоскости проекций проекция фигуры не изменяется. Если П₁П₂, то A₁B₁C₁ = A₂B₂C₂ (рис.1.4).

Рис.1.4 Рис.1.5

Свойства ортогонального проецирования

Наряду со свойствами параллельного (косоугольного) проецирования ортогональное проецирование имеет следующие свойства.

1. Отрезок прямой в общем случае равен гипотенузе прямоугольного треугольника, у которого один катет равен его проекции на данную плоскость проекции, а второй - разности расстоянии концов отрезка до этой плоскости (рис.1.5).

2. Любой отрезок прямой и плоская фигура, параллельные плоскости проекций, проецируются на эту плоскость без искажения (рис.1.6), например, если АВ  П₁, то A₁B₁ = AB ; ABC П₁, то A₁B₁C₁ = ABC.

Рис.1.6 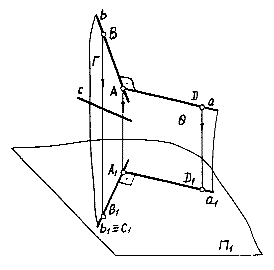Рис.1.7

3. Проекция любой фигуры (плоской фигуры, отрезка прямой и т.д.) не может быть больше самой фигуры (как следствие п. 1 и 2).

4. Ортогональные проекции двух взаимно перпендикулярных прямых, одна из которых параллельна плоскости проекций, а другая не перпендикулярна ей, взаимно перпендикулярны, т.е., если a  b, и a  П₁, то a₁ b₁ (рис.1.7). Пусть дано a b. Построим проекцию a b на П₁. AA₁ П₁ (как проецирующий луч), следовательно, плоскость Г (AA₁ b) также перпендикулярна П₁. Прямая а перпендикулярна плоскости Г, так как она перпендикулярна двум прямым AA₁ и b, принадлежащим плоскости Г. Но a₁ a (a П₁) и, следовательно, a Г, откуда A₁ перпендикулярна любой прямой плоскости Г, в том числе и b₁. Отсюда справедливо, что a₁ b₁.  Это доказательство относится как к пересекающимся прямым, так и к скрещивающимся. Как видно из чертежа, если с Г, а Г , то c₁ a₁.