Учебник Начерт. геометрия новый

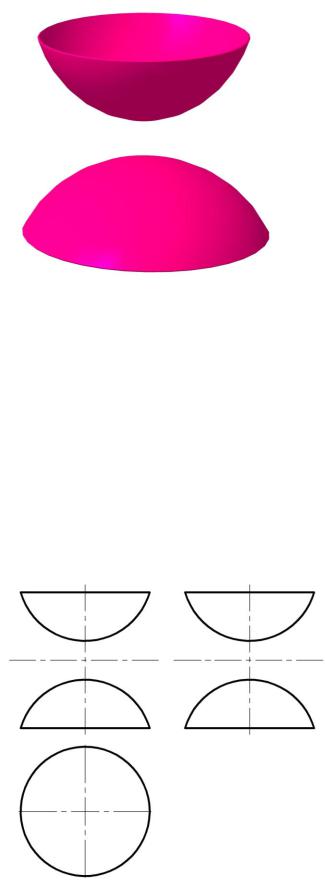
Рис. 9.15

Если a = b, то такая поверхность называется гиперболоидом вращения. Однополостный гиперболоид вращения может быть получен вращением гиперболы вокруг ее мнимой оси, двухполостный – вокруг действительной. Двухполостный гиперболоид вращения также является геометрическим местом точек P, модуль разности расстояний от которых до двух заданных точек A и B постоянен:

AP − BP | = const.

В этом случае A и B называются фокусами гиперболоида. Комплексный чертеж двухполостного гиперболоида представ-

лен на рис. 9.16.

Рис. 9.16

201

Чертежи на рис. 9.6 и 9.8 дают представление об ортогональных проекциях тора, на рис. 9.10 – сферы. Так как поверхности вращения, изображенные на этих рисунках, симметричны относительно оси i, то их проекции симметричны на тех плоскостях, которым перпендикулярна ось вращения. Поэтому можно вычерчивать не всю проекцию, а лишь ее половину, и даже четверть, как это будет показано ниже (конечно, если условия задачи не требуют изображать ее полностью).

Когда в качестве образующей выступает эллипс, то центр поверхности (точка, в которой все хорды, через нее проходящие, делятся пополам) помещен в начале системы координат, а за оси координат взяты оси симметрии поверхности (при этом координатные плоскости являются плоскостями симметрии), поверхностью вращения будет эллипсоид, описываемый в канонической форме уравнением

, где a, b, c – полуоси.

Если a=b>c, имеем сжатый (сплющенный) эллипсоид вращения,

который получается от вращения вокруг малой оси эллипса, лежащего в плоскости xOz. Если a=b<c, то имеем вытянутый эллипсоид вращения (рис. 9.17, а), получающийся от вращения вокруг большой оси эллипса, лежащего в плоскости xOz. Комплексный чертеж вытянутого эллипсоида представлен на рис. 9.17, б. Уравнение поверхно-

сти вытянутого эллипсоида:

b2 (x2 + y2) + a2 z2 = a2 b2.

Рис. 9.17, а

202

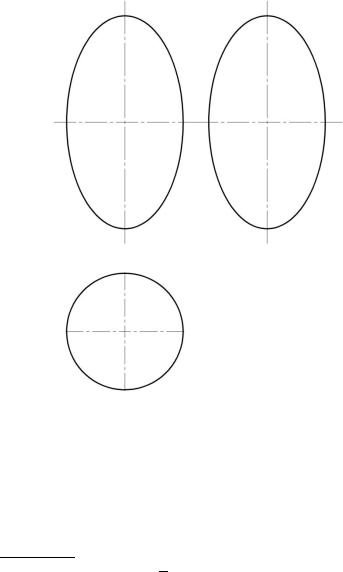
Рис. 9.17, б

Любая плоскость пересекает эллипсоид по эллипсу (в частном случае – по окружности).

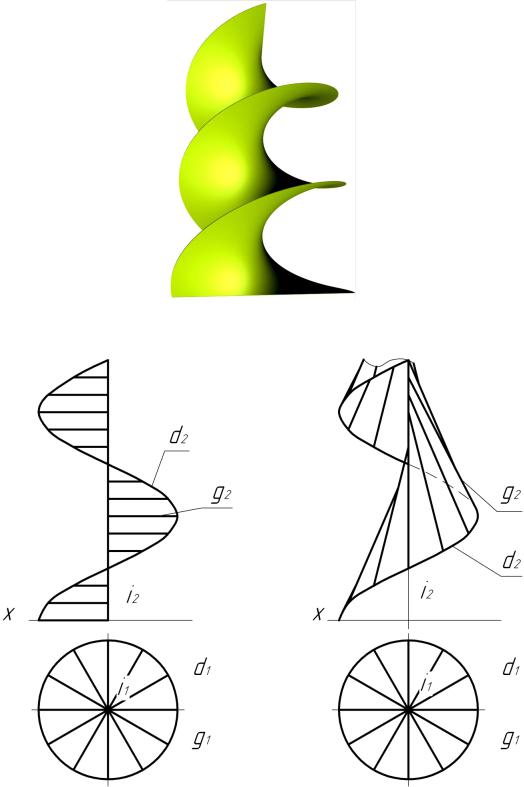
Винтовые поверхности (рис.9.18) образуются путем винтового перемещения образующей. Приведем уравнение винтовая поверхности:

, где р – винтовой параметр. Винтовая линия постоянного шага, образованная на поверхно-

сти прямого кругового цилиндра называется гелисой. Поэтому линейчатые винтовые поверхности, у которых направляющей является гелиса, называются геликоидами. Геликоиды называют прямыми, если угол наклона образующей к оси геликоида прямой. В противном случае геликоиды называются косыми.

У косого геликоида образующая, перемещаясь по направляющим, остается параллельной образующим конической поверхности (рис. 9.19, б). Тогда говорят о поверхности параллелелизма. Форма прямого геликоида используется при создании винтовых лестниц, шнеков, а также в прямоугольных резьбах, предназначенных для передачи значительных осевых усилий.

Косые геликоиды (рис. 9.19, б) ограничивают поверхность витков резьбы с прямолинейной боковой стороной профиля.

203

Выделение этих поверхностей показывает на особое значение их в технике, архитектурно-строительной практике и особенно в машиностроении.

Рис. 9.18

а

б

Рис. 9.19

204

9.3. Пересечение тел вращения с плоскостью частного положения

Так как все точки тела вращения описывают при своем движении окружности, то линия пересечения с плоскостью тел вращения будет окружностью. Если плоскость пересекает тело не перпендикулярно, то в зависимости от поверхности и расположения плоскости получаются различные линии. При построении линии пересечения первоначально определяют экстремальные (или опорные) точки (самая левая, правая, нижняя, верхняя, ближняя, дальняя точки), принадлежащие линии пересечения.

9.3.1. Пересечение цилиндра плоскостью, не перпендикулярной его оси

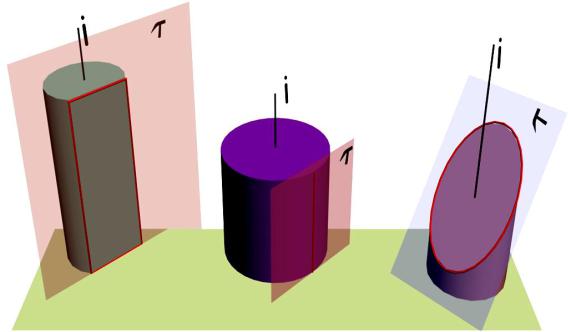
На рис. 9.20 показаны различные случаи положения плоскости сечения относительно оси вращения цилиндра.

а

б

в

Рис. 9.20

Если плоскость параллельна оси цилиндра, получим либо две параллельные прямые (рис. 9.20, а), либо одну прямую (рис. 9.20, б), которая совпадает с образующей (касательная плоскость).

205

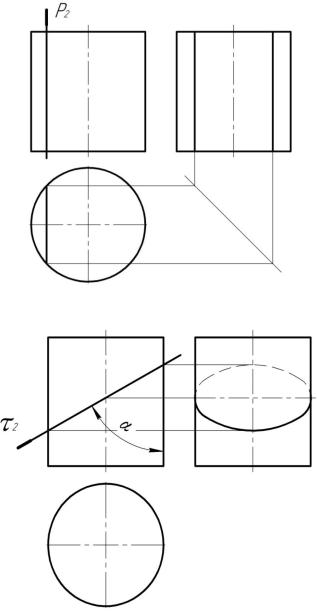
На рис. 9.21, а показан комплексный чертеж линии пересечения цилиндра с плоскостью, параллельной оси вращения. В данном случае линии пересечения на фронтальной проекции конкурируют друг с другом, а на профильной плоскости проекций они будут видимыми. Если бы секущая плоскость прошла правее оси цилиндра, то тогда эти линии были бы невидимыми.

При пересечении цилиндра с плоскостью, не параллельной и не перпендикулярной оси, получим эллипс (рис. 9.20, в), малая ось которого равна диаметру цилиндра, а большая – d/sin . На рис. 9.21, б эллипс принадлежит фронтально проецирующей плоскости, а значит, его большая ось будет проецироваться в виде отрезка прямой линии.

а

б

Рис. 9.21

206

Для случая, показанного на рис. 9.21, б, горизонтальная проекция линии пересечения – окружность, фронтальная – отрезок, соответствующий натуральной длине большой оси эллипса, малая ось равна диаметру цилиндра. На профильной плоскости проекций линия пересечения с плоскостью выглядит как эллипс, одна из осей которого d, а другая – d·ctg , где d – диаметр цилиндра, угол – угол наклона плоскости к оси цилиндра (рис. 9.21, б), большая ось – диаметр цилиндра.

Часть эллипса, находящаяся на фронтальной проекции правее оси цилиндра, будет невидима на профильной проекции, так как направление взгляда на профильную плоскость проекций слева направо.

9.3.2. Пересечение конуса плоскостью

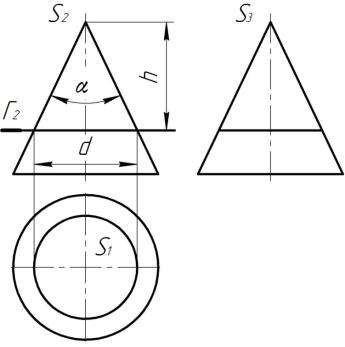
Если плоскость перпендикулярна оси вращения, то линией пересечения будет окружность с диаметром, равным

d = 2h tg /2.

Рис. 9.22

Пересечение конуса с плоскостью, не перпендикулярной оси вращения, дает несколько вариантов линий.

207

1. Точка – плоскость проходит через вершину конуса

(рис. 9.23).

Рис. 9.23

2. Прямая – плоскость касается поверхности конуса (рис. 9.24).

Рис. 9.24

3. Две пересекающиеся прямые – плоскость проходит через вершину конуса, а угол наклона плоскости по отношению к оси вращения меньше угла наклона образующей конуса к его оси (рис. 9.25).

208

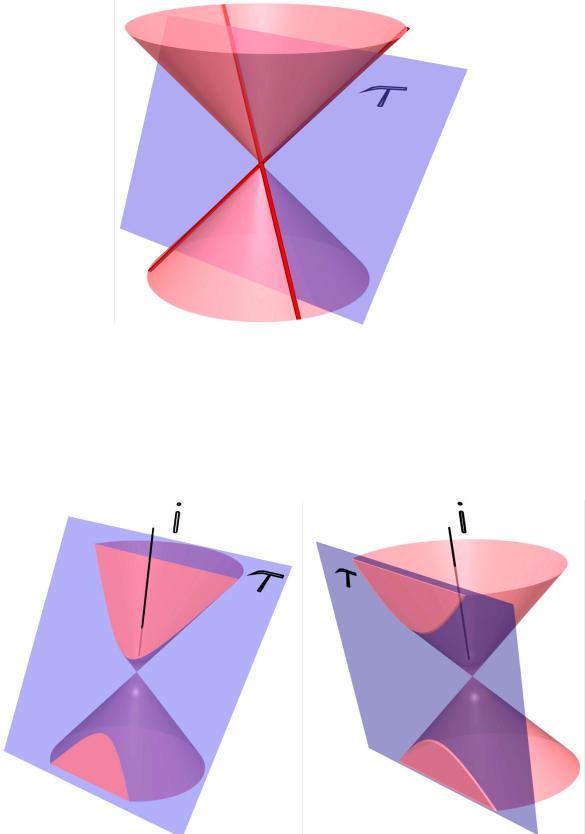
Рис. 9.25

4. Гипербола – плоскость пересекает верхнюю и нижнюю ветви конической поверхности (рис. 9.26). Плоскость параллельна оси конуса (рис. 9.26, а) или угол ее наклона меньше угла наклона образующей конуса к его оси, но при этом плоскость не проходит через вершину конуса.

а

б

Рис. 9.26

209

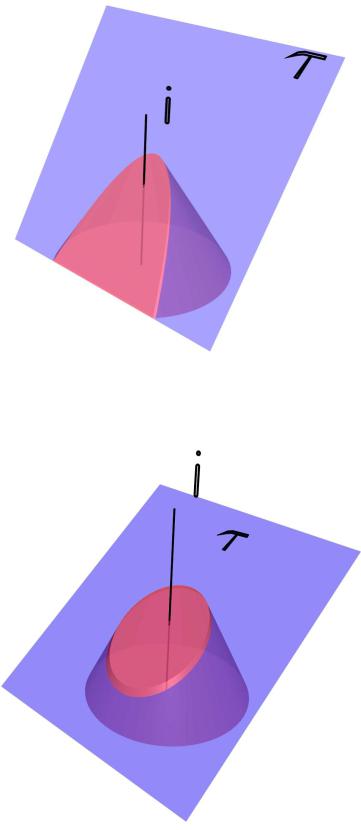
5. Парабола – плоскость не проходит через вершину конуса и параллельна образующей (рис. 9.27).

Рис. 9.27

6. Эллипс – плоскость пересекает только одну из ветвей конической поверхности (рис. 9.28).

Рис. 9.28

210