Учебник Начерт. геометрия новый

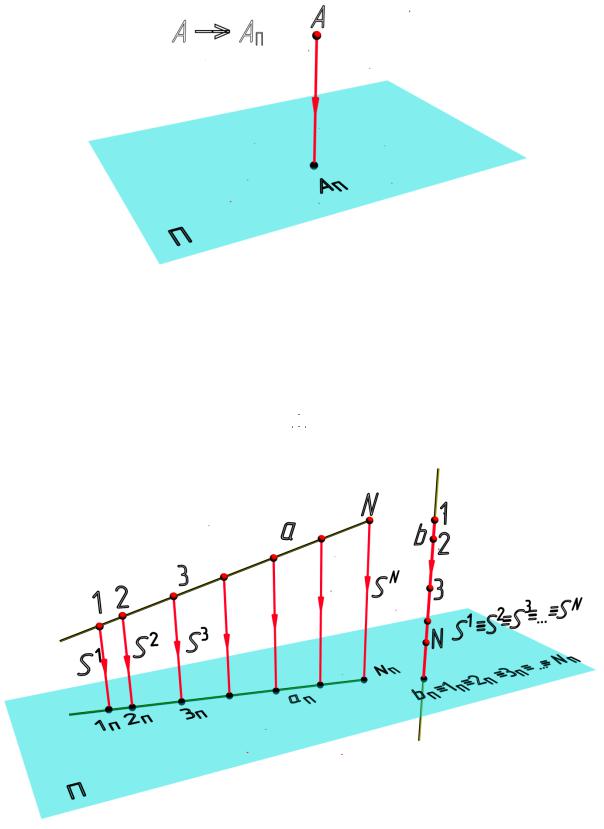
Рис. 2.8

Свойство 2. Проекция прямой линии на плоскости есть прямая (рис. 2.9, прямая а); в частном случае, когда прямая перпендикулярна плоскости проекции, – точка (рис. 2.9, прямая b):

( а) (а 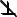П): а аП.

Рис. 2.9

21

Свойство 3. Если точка принадлежит (инцидентна) линии, то проекция точки принадлежит проекции этой линии (рис. 2.10):

А а АП аП.

Рис. 2.10

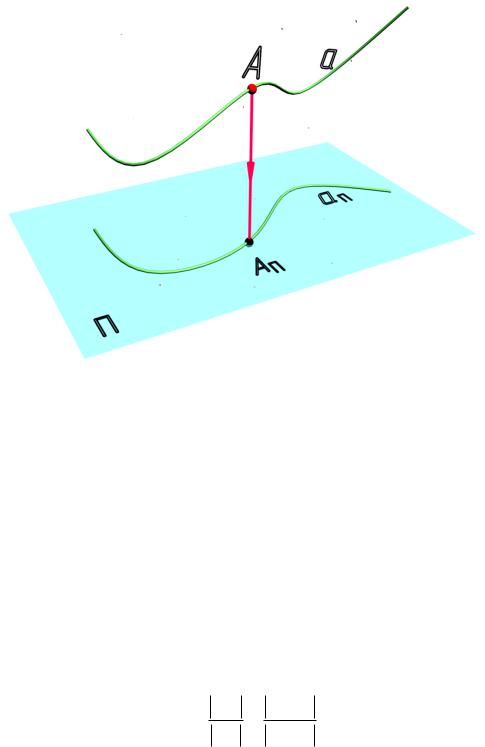
Свойство 4. Если точка делит отрезок прямой линии в какомлибо отношении, то и проекция отрезка делится проекцией точки в том же отношении (рис. 2.11):

C [ AB]

AC

A C

.

CB

C B

Докажем это свойство. Пусть отрезок [AB] прямой линии делится точкой С в отношении АС / СВ (рис. 2.11). Исходя из подобия треугольников АDC и CEB, можно записать AD / CE = AC / CB . Учитывая, что АD = АПСП и CE = CПBП , окончательно получим следующее свойство:

AC A C .

CB C B

22

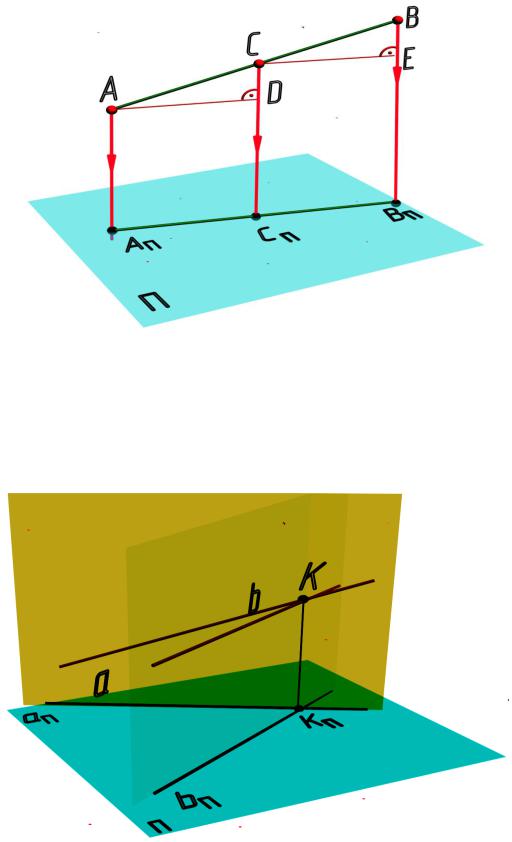
Рис. 2.11

Свойство 5. Точка пересечения проекции двух пересекающихся линий является проекцией точки пересечения этих линий (рис. 2.12).

K= a ∩ b KП = aП ∩ bП.

Рис. 2.12

23

Свойство 6. Проекции отрезков параллельных и не перпендикулярных плоскости проекций прямых параллельны, а их длины находятся в таком же отношении, как и длины этих отрезков:

[AB] ׀׀ [CD] ([AB]

П) [AПBП] ׀׀ [CПDП]

AB

A B

.

CD

C D

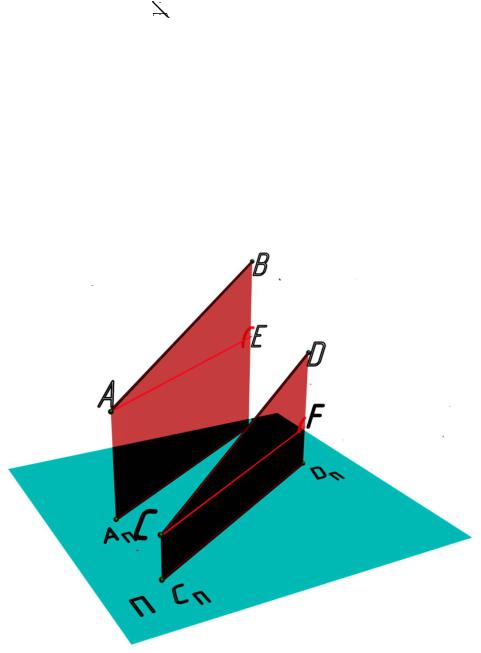
Справедливость последнего утверждения понятна из рис. 2.13. Два отрезка принадлежат двум параллельным проецирующим плоскостям (забегая вперед, отметим, что проецирующие плоскости перпендикулярны к плоскости проекций, поэтому проецируются в виде прямой линии). Отсюда делаем вывод о параллельности проекций. Наконец, из подобия треугольников АВЕ и CDF получаем пропорциональность их сторон.

Рис. 2.13

Свойство 7. Проекции двух скрещивающихся (непересекающихся) прямых линий могут или пересекаться (рис. 2.14, а), или быть параллельными (рис. 2.14, б):

( а b) (aП ∩ bП) (aП ׀׀bП).

24

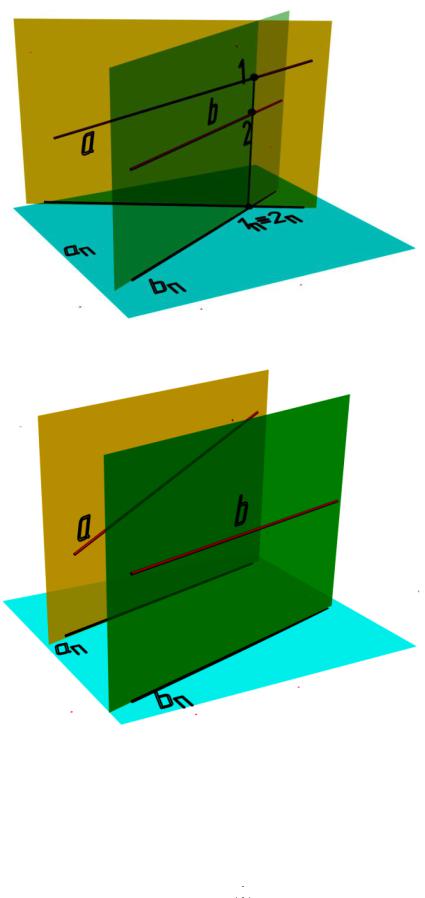
а

б

Рис. 2.14

Свойство 8. Прямой угол проецируется без искажения (прямым углом), если одна из его сторон параллельна плоскости проекций, а другая не перпендикулярна ей (рис. 2.15):

(a b) (a ׀׀ П, b П) (aП bП).

25

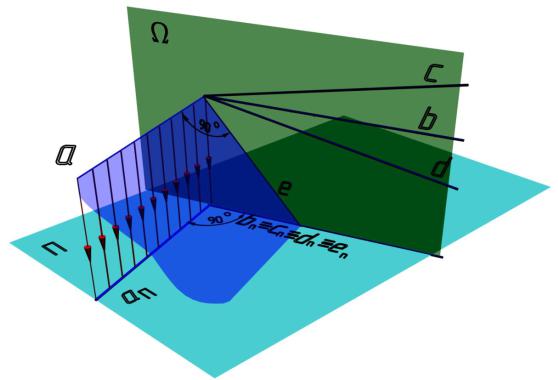
Рис. 2.15

Расположим прямой угол, образованный прямыми а и b, в плоскости, параллельной плоскости проекций П как показано на рис. 2.15. Через прямую b проведем плоскость Ω, перпендикулярную плоскости П. Все прямые, лежащие в плоскости Ω, будут образовывать угол 90 с прямой а. Таким образом, при вращении прямой b вокруг прямой а (положение с, d и е) на плоскости П будет проецироваться одна и та же линия. Причем проекция прямой а на эту же плоскость будет перпендикулярна всем проекциям прямых, лежащих в плоскости Ω, так как а параллельна плоскости проекций П.

Следует отметить, что в виде прямого угла проецируется любой другой угол, у которого стороны лежат во взаимно перпендикулярных плоскостях. Если ни одна из сторон угла не будет параллельна плоскости проекций и он не принадлежит проецирующей плоскости, то прямой угол будет проецироваться в виде тупого (рис. 2.16) или острого (рис. 2.17) угла. Кроме того, проекция тупого или острого угла может выглядеть как прямой угол. Так, на рис. 2.18 тупой угол проецируется как прямой, а на рис. 2.19 прямым будет острый угол, спроецированный на плоскость проекций.

26

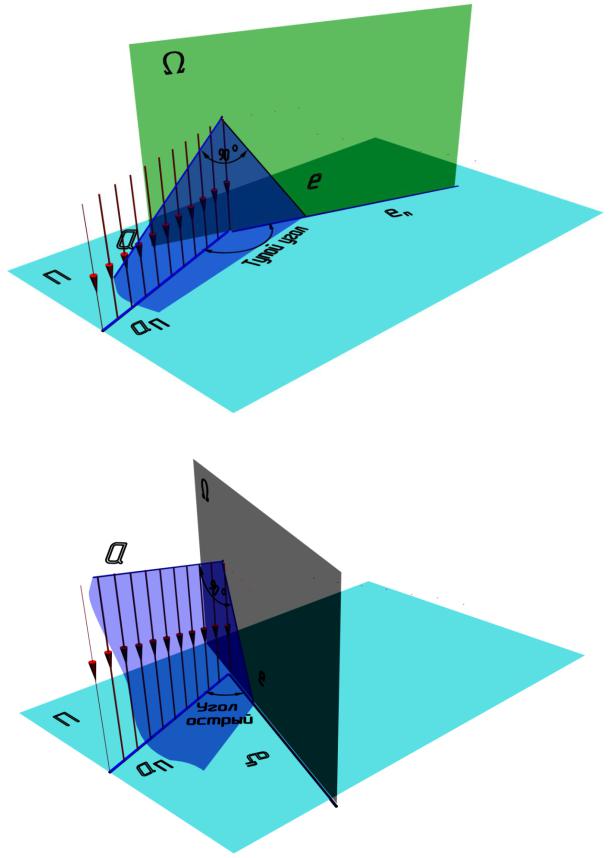
Рис. 2.16

Рис. 2.17

27

Рис. 2.18

Рис. 2.19

Итак, перпендикуляр к прямой проецируется как перпендикуляр к проекции прямой, когда либо прямая параллельна плоскости проекций, либо перпендикуляр параллелен плоскости проекций, либо плоскости проекций параллельны обе прямые.

28

Свойство 9. Плоская фигура, параллельная плоскости проекций, проецируется на эту плоскость без искажения (рис. 2.20):

Ф ׀׀ П ФП Ф.

Рис. 2.20

Свойство 10. При параллельном перемещении фигуры или плоскости проекций фигуры не меняются (рис. 2.21):

( ) ( ׀׀ Ф) ФП .

Рис. 2.21

29

Вопросы и задания для самопроверки

1. Объяснить сущность центрального проецирования.

2. Что такое параллельное проецирование? Привести примеры косоугольного и ортогонального проецирования.

3. Перечислить инварианты ортогонального проецирования.

4. При каких условиях прямой угол проецируется без искаже-

ния?

5. В каком случае плоская фигура проецируется на плоскость проекций без искажения?

6. Может ли проекция острого или тупого угла выглядеть как прямой угол?

7. Каковы преимущества ортогонального проецирования перед центральным и параллельным?

8. Какие элементы определяют аппарат центрального и какие параллельного проецирования?

9. Какую точку называют несобственной?

10. Какие свойства геометрических тел называются инвариантными?

3.ТОЧКА

Вначертательной геометрии любая фигура рассматривается как множество точек, точка – единственное множество.

Точка является элементом более сложных фигур, таких как прямая, плоскость, поверхность. Поэтому изучение построения чертежей начинают с построения точки на плоскостях проекций и ее пространственного изображения в заданной системе координат.

3.1.Система координат

Координатные плоскости проекций

Все геометрические образы будем рассматривать относительно прямоугольной (декартовой) системы координат, состоящей из трех взаимно перпендикулярных осей (рис. 3.1): ось x – ось абсцисс; ось y

– ось ординат; ось z – ось аппликат. Начало координат – точка пересечения осей, обозначается буквой О. Такая система координат образует правую тройку осей: если смотреть навстречу оси z, то поворот оси x к оси y будет против хода часовой стрелки.

30