3. Логические функции двух переменных

Областью определения логической функции nпеременных является совокупность комбинаций этих переменных. Так как дляn-разрядного двоичного числа имеется всего 2ⁿразличных комбинаций, то область определения логической функцииnпеременных состоит изm=2ⁿточек. Поскольку в каждой позиции (точке) функция может принимать значение 0 или 1, то, следовательно, дляnпеременных может быть составлено 2^m логических функций. Например, при двух переменных Х₁,Х₂ область определения функции состоит из 2²= 4 точек (00, 01, 10, 11), и мы имеем 2⁴= 16 логических функций. Некоторые из этих функций зависят не от всех аргументов. Такие функции называютсявырожденными.

Х1 Х2	0 0	0 1	1 0	1 1	Значения аргументов
f0	0	0	0	0	f0 Вырожденная функция - константа 0
f1	0	0	0	1	f1 = X1  X2 Лог. функция И
f2	0	0	1	0	f2 = X1  X2 “Запрет по Х2”
f3	0	0	1	1	f3 = X1 вырожденная (поглощение X2)
f4	0	1	0	0	f4 = X1  X2 “Запрет по Х1”
f5	0	1	0	1	f5 = X2 вырожденная (поглощение X1)
f6	0	1	1	0	f6 = X1  X2  X1  X2 слож. по мод. 2
f7	0	1	1	1	f7 = X1  X2 логическая функция ИЛИ
f8	1	0	0	0	f8 = X1  X2 логическая функция ИЛИ-НЕ
f9	1	0	0	1	f9 = X1X2  X1 X2 функция равнозначности
f10	1	0	1	0	f10 = X2 вырожденная
f11	1	0	1	1	f11 = X1  X2 импликация Х2 в Х1
f12	1	1	0	0	f12 = X1 вырожденная
f13	1	1	0	1	f13 = X1  X2 импликация Х1 в Х2
f14	1	1	1	0	f14 = X1  X2 Лог. функция И-НЕ
f15	1	1	1	1	f15 Вырожденная функция - константа 1

4. Алгебраическое представление логических функций

Мы уже знаем, что логическая функция может быть представлена:

а) словесно: если Х₁=1 и X₂=1, то Y=1;

б) таблично: в виде таблицы истинности, которая содержит n+mстолбцов и 2ⁿстрок (n-число входов или аргументов,m-число выходов);

i	X1	X2	Y
0	0	0	0
1	0	1	0
2	1	0	0
3	1	1	1

в) с помощью карт Карно (или диаграмм Вейча), которые представляют собой разновидность табличной формы задания логической функции;

г) числовым способом: когда функция задается в виде набора (множества) десятичных чисел, соответствующих номерам набора аргументов, при которых функция принимает значение 1;

Например, функция ИЛИ для аргументов Х₁, Х₂;

Y	X1	X2
0	0	0
1	0	1
1	1	1
1	1	1

Y=1,2,3_X1X2.

=0 Переменные указывают порядок

=1 формирования битов двоичного числа.

=2

=3 Для логической функции И Y=3_X1X2;

д) аналитически: в виде алгебраического выражения.

Рассмотрим более подробно алгебраическое представление логической функции.

Введем понятие терма. Термом обозначим функцию:

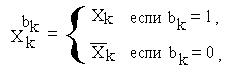
где: к = 0,1, ...,n ,

b_k - константа 0 или 1.

При любом фиксированном значении переменной X_k=a_kсправедлива формула:

_

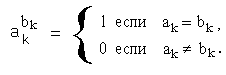
Действительно: 0⁰=0=1; 1¹=1;

_

0¹=0 ; 1⁰= 1=0.

Используя введенное обозначение, запишем функцию И (конъюнкцию) nлогических переменных:

Эта функция принимает значение 1 только при одном наборе значений переменных (а₁,а₂, ...,а_n), для которого выполняется условие a_k=b_k, для всех остальных наборов функция принимает значение 0.

Например: __ __

F(X₁,X₂, ...,X₅)=X₁X₂X₃X₄X₅=X⁰₁X¹₂X⁰₃X¹₄X¹₅

принимает значение 1 только при одном наборе переменных (0,1,0,1,1).

Конъюнкция, в которую входят все переменные (аргументы логической функции) в прямой или инверсной форме, называется минтермом.

Минтерм обозначим C¹_i , где i-номер единственного набора, на котором C¹_i=1 (пример выше: 01011₂=11₁₀, следовательно - C¹₁₁).

Алгебраически минтерм представляют в виде конъюнкции, в которую в прямой форме входят все переменные, имеющие в данном наборе значение 1, и в инверсной форме все переменные, имеющие в данном наборе значение 0.

Для логической функции двух переменных можно составить следующие минтермы:

i	X1	X2	__ __ C^10=X1X2	__ C^11=X1X2	__ C^12=X1X2	C^13=X1X2
0	0	0	1	0	0	0
1	0	1	0	1	0	0
2	1	0	0	0	1	0
3	1	1	0	0	0	1

Аналогично можно рассмотреть функцию ИЛИ (дизъюнкцию) n логических переменных:

Логическая функция ИЛИ принимает значение F()=1, если хотя бы одна переменная Х^bi_i=1. Следовательно, существует только один набор значений переменных, для которых выполняется условие a_kb_k, при котором функция принимает значение 0.

Например, функция: __ __

F(X₁,X₂,X₃,X₄,X₅)=X₁X₂X₃X₄X₅=X¹₁X¹₂X¹₃X⁰₄X⁰₅

принимает значение 0 только при одном наборе (0,0,0,1,1).

Дизъюнкцию, в которую входят все переменные в прямой или инверсной форме, называют макстермом.

Макстерм имеет обозначение C⁰_i , где i-номер единственного набора, при котором C⁰_i=0.

Рассмотренный выше пример: 00011₂= 3₁₀, следовательно - C⁰_{3 .}

Рассмотрим макстермы двух переменных:

i	X1	X2	C^00=X1 X2	__ C^01=X1X2	__ C^02=X1X2	__ __ C^03=X1X2
0	0	0	0	1	1	1
1	0	1	1	0	1	1
2	1	0	1	1	0	1
3	1	1	1	1	1	0

Макстерм представляется в виде дизъюнкции, в которую в прямой форме входят все переменные, имеющие на данном наборе (при котором C⁰_i=0) нулевые значения, и в инверсной форме - все переменные, имеющие на данном наборе значение 1.

Аналогично функциям И, ИЛИ можно ввести функцию И-НЕ для n переменных:

_____ ____________________ ________________

Эта функция, являясь инверсией конъюнкции n переменных, принимает значение 0 только на одном наборе переменных, для которого a_k=b_{k .}Для всех остальных наборов эта функция равна 1.

И, наконец, можно определить функцию ИЛИ-НЕ:

_____ ___________________ ________________

Эта функция принимает значение 1 только на одном наборе значений переменных, для которого a_kb_k, на всех остальных наборах эта функция равна 0.