4.1. Трехмерные примитивы

Предметом трехмерной компьютерной графики являются различные пространственные объекты. По геометрическим свойствам их можно разделить на следующие виды:

• точки в пространстве;

• пространственные линии и отрезки линий;

• поверхности;

• многогранники;

• геометрические тела сложной формы.

Для синтеза реалистичных изображений кроме геометрии объектов необходимо также моделировать распространение света, что заставляет задавать и использовать ряд физических свойств объектов и всей пространственной сцены. К ним относятся расположение и яркость источников света, цвета и степень зеркальности (гладкости) поверхностей объектов, коэффициенты преломления света на границах прозрачных сред, степень их прозрачности и др.

Геометрия трехмерных примитивов, как и двумерных, описывается алгебраическим и параметрическим методами. Ниже в качестве примитивов будут рассмотрены точки, линии, поверхности и многогранники.

Tочка P в пространстве задается своими координатами (x, y, z). В трехмерной компьютерной графике традиционно используют левостороннюю систему координат, показанную на рис. 4.1. Причем изображение строится на плоскости OXY, называемой картинной плоскостью. На нее проецируются изображаемые объекты.

Н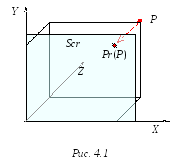а рис. 4.1 Pr(P) означает проекцию точки P на картинную плоскость. Часть этой плоскости, соответствующая экрану монитора, обозначена как Scr.

Для задания линий в пространстве используется алгебраическая и параметрическая формы.

В алгебраической форме линия в пространстве задается как пересечение двух поверхностей, что представляется в виде системы алгебраических уравнений

(4.1)

Пространственные кривые в параметрической форме отличаются от плоских, рассмотренных в п. 2.3, 2.4, лишь тем, что изменение координаты z задается третьей функция z(t):

(4.2)

Формулы и выводы, приведенные в п. 2.3, 2.4, несложно модифицировать для описания кубических сплайнов и кривых Безье в пространстве.

Поверхности, как и линии, задаются в алгебраической и параметрической формах. Алгебраическая поверхность описывается уравнением вида F(x, y, z) = 0. Например, уравнение сферической поверхности с центром в начале координат и радиусом R имеет вид

x² + y² + z² – R² = 0. (4.3)

В параметрической форме задаются четырехугольные куски S(u,v) произвольных гладких поверхностей (рис. 4.2). Закон изменения каждой из координат поверхности должен быть описан своей функцией от двух параметров u и v:

(4.4)

Как и для параметрических кривых, в качестве области изменения параметров u и v обычно используют интервал [0, 1], т.е. 0  u  1, 0  v  1.

Рис. 4.2

При интерактивном синтезе параметрических поверхностей для функций x(u, v), y(u, v) и z(u, v) используют те же полиномиальные базисы, что и в двумерной графике. Разработаны математическая теория и алгоритмы для создания полиномиальных кубических поверхностей, поверхностей Безье и других видов полиномиальных сплайн-поверхностей [7, 8].

В то же время для задания некоторых видов поверхностей удобнее использовать другие базисы. Так, особым классом поверхностей являются поверхности вращения [7]. Поверхностью вращения называется поверхность, образованная вращением плоской кривой вокруг неподвижной оси, лежащей в одной плоскости с кривой. Например, функция

(4.5)

определяет поверхность, описанную вращением кривой P(u) = [x(u) z(u)], заданной в плоскости OXZ, вокруг оси OZ (рис. 4.3).

Рис. 4.3

Другим примером поверхности вращения может служить сферическая поверхность радиусом R с центром в начале координат, описываемая следующим образом:

(4.6)

Отметим, что параметры u и v определяют на поверхности географическую систему координат, в которой u является долготой, а v – широтой. Полюса этой сферы расположены на оси OZ.