Лекция 14 теорема об изменении кинетической энергии механической системы Третья мера движения  кинетическая энергия механической системы

Кинетической энергией материальной точки называется скалярная величина, равная половине произведения массы точки на квадрат ее скорости. Кинетической энергией механической системы называется сумма кинетических энергий точек этой системы:

. (14.1)

Кинетическая энергия абсолютно твердого тела соответственно равна

,

где интеграл, записанный условно, берется по массе всего тела.

Если известны уравнения движения всех точек механической системы , то кинетическую энергию системы можно вычислить по формуле

.

Вычислим кинетическую энергию механической системы, участвующей в сложном движении.

Рис. 14.1

Введем как и в предыдущей лекции в центре масс механической системы кёнингову систему координат Сx2y2z2, которая движется поступательно относительно инерциальной системы отсчета Оxyz, (рис.14.1). Учитывая, что абсолютная скорость kой точки равна и , имеем

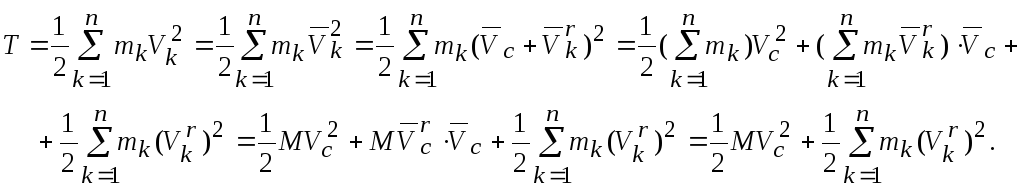
Далее обозначая кинетическую энергию относительного движения механической системы относительно кёнинговых осей

,

получим

(14.2)

Таким образом, доказали теорему Кёнига: кинетическая энергия механической системы в её абсолютном движении равна сумме кинетической энергии, которую имела бы материальная точка, расположенная в центре масс системы и имеющая массу, равную массе системы и кинетической энергии движения системы относительно центра масс.

Вычисление кинетической энергии при различных движениях

Твердого тела

Будем приближенно моделировать твердое тело неизменяемой системой n материальных точек, распределенных по объему тела.

1. Поступательное движение твёрдого тела.

Учитывая, что при поступательном движении твёрдого тела скорости всех его точек равны и вынося квадрат скорости за знак суммирования, получим

.

Таким образом,

, (14.3)

где  масса тела.

В формуле (14.3) отсутствует знак суммирования, и, следовательно, она справедлива и для твердого тела с непрерывно распределенной массой.

2. Вращательное движение твёрдого тела вокруг неподвижной оси.

Учитывая, что при вращательном движении тела скорость точки тела , где  угловая скорость тела,  расстояние от точки до оси вращения, кинетическая энергия тела равна

. (14.4)

Вынося квадрат угловой скорости за знак суммирования в равенстве (14.4), получим:

,

где  момент инерции тела относительно оси вращения z. Cледовательно,

(14.5)

Для твердого тела с непрерывно распределенной массой сумма в выражении для момента инерции относительно оси вращения перейдет в

соответствующий интеграл.

3. Плоскопараллельное движение твёрдого тела.

Так как, введением осей Кёнига плоское движение раскладывается на переносное поступательное вместе с осями Кёнига и относительное вращательное движение тела относительно осей Кёнига, то на основании теоремы Кёнига

, (14.6)

где  момент инерции тела относительно оси происходящей через центр масс С тела перпендикулярно плоскости движения тела.