1.3. Свойства функции распределения.

а) Интеграл этой функции по всему фазовому пространству равен единице:

. (1.3.1)

Действительно, система в любой момент времени обязательно находится в каком-то микросостоянии, это событие достоверное.

б) Функция распределения обладает свойством мультипликативности. Разделим мысленно большую систему на две подсистемы. и– соответствующие элементы объёма в фазовом пространстве этих подсистем. Энергия взаимодействия подсистем мала по сравнению с её внутренней энергией. Такие подсистемы называются квазизамкнутыми. Поскольку различные подсистемы слабо взаимодействуют друг с другом, то их можно считать независимыми и в статистическом смысле (статистически независимыми). Статистическая независимость означает, что состояния одной из подсистем никак не влияет на вероятности различных состояний другой подсистемы. Вероятность составной (большой) систем находиться в элементе фазового объёмаи можно выразить (представить), как произведение вероятностей нахождения каждой из подсистем соответственно в и.

.

Поскольку , то

(1.3.2)

Здесь – функция распределения составной системы,и– функции распределения отдельных подсистем.

1.4. Уравнение Лиувилля, теорема Лиувилля.

Для функции распределения микросостояний в фазовом пространстве гамильтоновых систем справедливо уравнение Лиувилля:

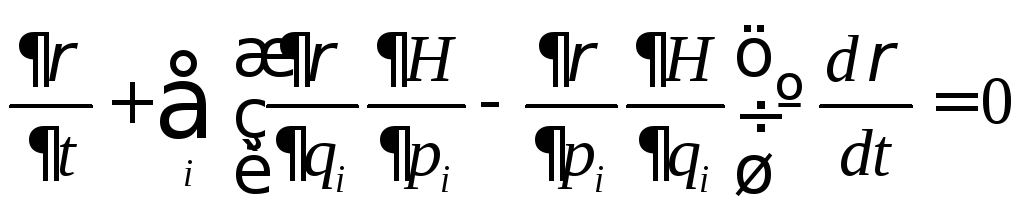. (1.4.1)

Теорема Лиувилля: функция распределения микроскопических состояний гамильтоновых систем постоянна вдоль фазовых траекторий. То есть для любых двух моментов времени

. (1.4.2)

Иногда удобнее пользоваться другой формулировкой этой теоремы. Пусть некоторая совокупность систем ансамбля в момент времени t₀ находится в микросостояниях, занимающих объём фазового пространства. К моменту времениt изображающие точки перемещаются в объём . Из условия сохранения числа системи соотношения (1.4.2) следует, что

. (1.4.3)

Для гамильтоновых систем фазовый объём произвольной области фазового пространства сохраняется, но может деформироваться, то есть менять свою форму.

1.5. Из теоремы Лиувилля следует, что функция распределения должна выражаться через такие комбинации обобщённых координат и импульсов, которые при движении системы остаются постоянными. Такие величины называют интегралами движения. Интегралов движения много, но аддитивных – семь: энергия, три компоненты вектора импульса, три компоненты вектора момента импульса.

Макроскопическую систему всегда можно рассматривать в такой системе отсчёта, в которой она покоится, и, следовательно, импульс и момент импульса её равны нулю. Остаётся один аддитивный интеграл движения – энергия. Поэтому логарифм функции распределения (аддитивная функция) может зависеть только от энергии:

. (1.5.1)

Следовательно, зависимость функции от переменныхисвязана только с зависимостью от этих переменных энергии.

1.6. Зная функцию распределения можно найти среднее по ансамблю значение физической величины (фазовое среднее):

. (1.6.1)

Считается, что временные и фазовые средние равны

. (1.6.2)

Системы, для которых выполняется это равенство, называются эргодичными.

Для Гиббса представление об ансамбле был удобным вычислительным приёмом для получения средних значений макроскопических величин. Дальнейшие работы по обоснованию статистической физики показали, что понятие ансамбля является более глубоким и важным. Необходимость понятия статистического ансамбля и статистического описания вытекает из свойства динамической неустойчивости движения частиц, а, следовательно, и фазовых траекторий, приводящего к перемешиванию. Неустойчивость проявляется в том, что существуют направления, вдоль которых расстояния между траекториями растут экспоненциально во времени. Очень малое изменение положения фазовой точки, выбранной за начальную, приводит к сильному расхождению соответствующих траекторий. Если движение финитно, то эти траектории не могут разойтись дальше, чем на размер области движения. Поэтому происходит их сильное запутывание, перемешивание. При наличии неустойчивости траектории, имеющие сколь угодно близкие начальные условия, ведут себя совершенно по-разному. Любое малое возмущение будет нарастать и дальнейший маршрут изобразительной точки невозможно предвидеть.

Микросостояние системы характеризуется некоторым набором чисел. Числа задаются с помощью конечного количества знаков, что ограничивает точность описания. Таким образом, состояние системы определяется не точкой в фазовом пространстве (для этого нужна бесконечно большая информация), а небольшой областью. Если фазовые траектории системы имеют сильную зависимость от начальных условий, точки этой области описывают совершенно различные траектории (рис.1).

Таким образом, вместо одной системы и одной фазовой траектории следует рассматривать ансамбль таких систем и ансамбль фазовых траекторий. Понятие ансамбля для систем с перемешиванием появляется естественным образом, потому что для таких систем возможно только статистическое описание. Ансамбль определяют, задавая плотность распределения вероятностей в фазовом пространстве (функцию распределения). Физически это соответствует рассмотрению ансамбля тождественных систем с различными начальными условиями.