1.7. Пример.

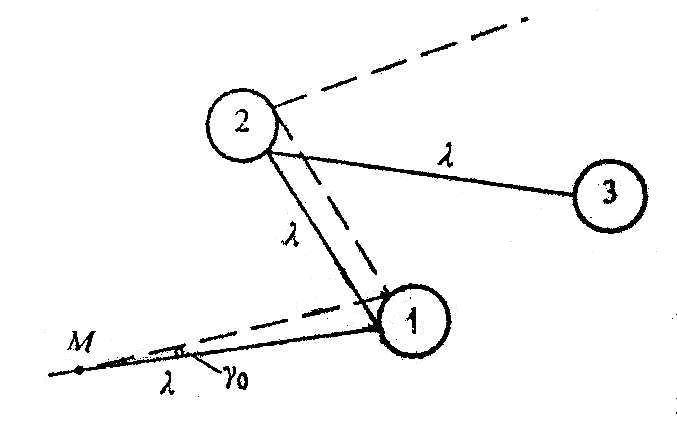
Рассмотрим природу возникновения молекулярного хаоса. Пусть молекула А сталкивается с другими молекулами газа. На рис.2 диски соответствуют поперечному сечению соударений этой молекулы с молекулами 1,2,3. Радиус каждого диска приближённо равен r, средняя длина свободного пробега – . В какой-то момент времени, который будем считать начальным, скорость молекулыА немного изменяется. На рис.2 сплошной линией изображена невозмущённая траектория молекулы, пунктирной – возмущённая. Она отклонена от невозмущённой на малый угол . Легко показать, что после одного соударения, которое считается упругим, уголвозрастает враз. Следовательно послеn соударений будем иметь

. (1.7.1)

Д

ля воздуха при нормальном атмосферном давлении длина свободного пробега молекулы газа равна около 10^-8 м, а её радиус – 10^-10 м. Поэтому .

С

Рис.2

оотношение (1.7.1) обычно записывают иначе. Пусть средняя длина вдоль траектории молекулы будет, гдеv – средняя её скорость и t – время движения. Тогда

, (1.7.2)

где . (,,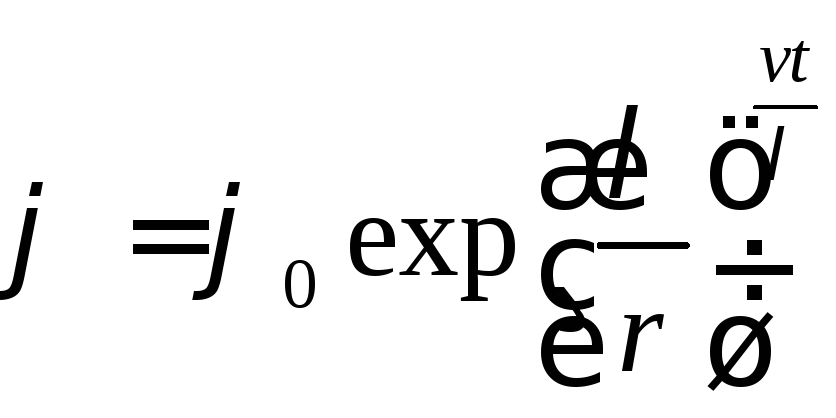,). Из соотношения (1.7.2) видно, что первоначально как угодно близкие траектории экспоненциально разбегаются, величинаk характеризует среднюю скорость их разбегания.

Таким образом, траектории молекул газа, которые очень чувствительны к начальным условиям, являются неустойчивыми. Они также чувствительны к возмущениям, вносимым внешним окружением. Можно говорить лишь о вероятности нахождения молекулы в том или ином месте занятого газом объёма. Равновесное макросостояние представляет собой совокупность микросостояний, каждое из которых неустойчиво и через короткое время заменяется другими микросостояниями.

1.8. Учёт квантовых свойств.

Квантовые свойства частиц сначала будем учитывать в квазиклассическом приближении. Это означает:

а) эволюцию микросостояний систем будем описывать фазовыми траекториями. Однако в квазиклассическом приближении считаются возможными только те траектории, которые соответствуют дискретным (квантованным) состояниям.

б) микросостоянию системы соответствует не фазовая точка, а, учитывая соотношение неопределённостей , ячейка размером, гдеf – число степеней свободы, N – число частиц.

Число квантовых состояний системы в интервале энергий от Е до (кратность вырождения):

. (1.8.1)

Здесь Г – фазовый объём, соответствующий состояниям с энергией меньшей или равной Е.

1.9. Распределения Гиббса.

Конкретный вид функции распределения микросостояний системы зависит от условий, в которых она (система) находится.

а) Микроканоническое распределение Гиббса.

Система изолирована, её энергия Е₀ фиксирована. Соответствующий ансамбль называется микроканоническим. Поэтому для системы возможны только такие фазовые траектории, на которых её энергия равна Е₀. Вероятность состояний с другими значениями энергий равна нулю. Поскольку в соответствии с теоремой Лиувилля, вдоль фазовых траекторий постоянна, то вероятность всех состояний, при которых энергия системы равнаЕ₀, одинакова:

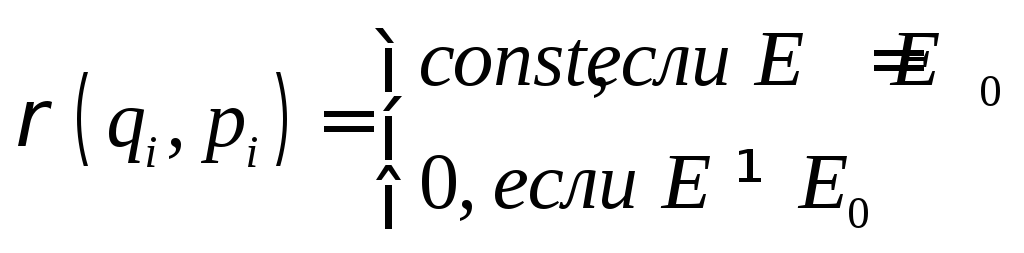. (1.9.1)

Функция распределения должна удовлетворять условию нормировки. Поэтому , где– дельта-функция Дирака (О-функции см. пособие «Операторы квантовой механики»).

Система со строго фиксированной энергией – слишком абстрактная модель. В природе не существует совершенно изолированных систем. Взаимодействие с внешней средой, хотя и очень слабое, всегда есть. В квантовой механике энергия точно определена (), если время жизни данного состояния системы бесконечно (). Поэтому обычно значение энергии системы указывают в узком интервале ().

Макросостоянию системы соответствует большое число микросостояний (допустимых квантовых состояний). Поскольку все микросостояния для изолированной системы равновероятны, вероятность того, что изолированная система находится в определённом макросостоянии, пропорциональна числу совместимых с ним микросостояний (по формуле сложения вероятностей). Поэтому микроканоническое распределение Гиббса можно записать так:

. (1.9.2)

б) Каноническое распределение Гиббса.

Подсистема находится в термодинамическом равновесии с термостатом. Термостатом называется система, температура которой при взаимодействии с подсистемой остаётся постоянной. Соответствующий ансамбль называется каноническим. Каноническое распределение Гиббса можно получить, если рассматривать подсистему с термостатом как одну изолированную систему и применить к ней микроканоническое распределение. При этом должны выполнятся условия:

1) (Е – энергия изолированной системы);

2) (– энергия взаимодействия подсистемы и термостата);

3) обмен частицами между подсистемой и термостатом отсутствует, число частиц в подсистеме постоянно.

Каноническое распределение Гиббса в квазиклассическом приближении можно записать в виде:

(1.9.3).

Здесь – вероятность того, что подсистема, составляющая малую часть изолированной системы, находится в одном из состоянийс энергией; параметр

(1.9.4)

называют модулем канонического распределения. Величина

(1.9.5)

есть энтропия. Здесь энтропия определена для равновесного состояния. Связь статистической энтропии и термодинамическойS:

. (1.9.6)

Постоянная k называется постоянной Больцмана (Дж/К). Если число микросостоянийинтерпретировать как меру неточности знаний о системе или как меру хаотичности, то энтропию также можно считать мерой хаотичности.

Свойства модуля канонического распределения:

1) является положительной величиной;

2) эта величина может относиться только к макросистемам;

3) равенство модулей подсистем является условием их теплового равновесия.

Поэтому величину называют статистической температурой:

. (1.9.7)

Из условия нормировки следует:

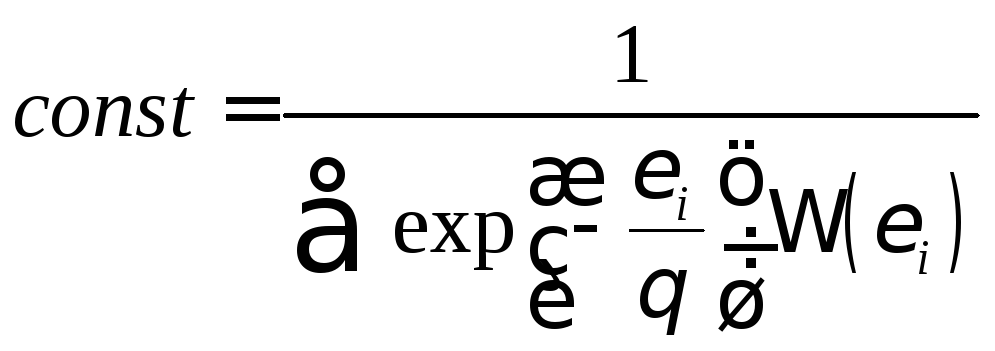. (1.9.8)

Выражение

(1.9.9)

называется статистической суммой или суммой по состояниям. Подставляя значение постоянной в выражение (1.9.3) получаем

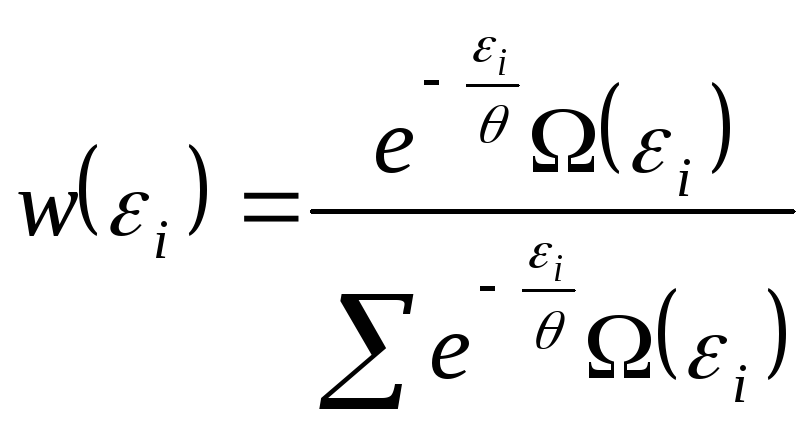. (1.9.10)

Из формул (1.9.3) и (1.9.10) следует, что в каноническом ансамбле энергия подсистемы, состоящей из большого числа частиц, определяется достаточно точно: распределение имеет резкий максимум при некотором значении энергии (наиболее вероятном значении энергии). В распределении есть экспоненциально убывающий множитель, однако число состояний для систем с большим числом частиц быстро растёт с энергией подсистемы. Например, если подсистемой является газ, состоящий изN одинаковых молекул, заключённых в сосуде, то . Произведение двух функций, зависящих от энергий: быстро убывающей и быстро возрастающей, приводит к возникновению у распределения Гиббса резкого максимума (рис.3).

Подавляющую часть времени подсистема будет проводить в состояниях с энергией близкой к .

Для макроскопической подсистемы

. (1.9.11)

Наиболее вероятное состояние вносит основную долю в среднее значение величин, характеризующих подсистему. Например, для энергии имеем: . (Принимаем. Соотношение (1.9.6) теперь можно переписать точнее:

. (1.9.12)

То есть энтропия макроскопической системы равна логарифму числа состояний системы, находящейся в состоянии равновесия.

Выразим также статистическую сумму через среднюю энергию подсистемы:

. (1.9.13)

Каноническое распределение Гиббса в классическом приближении:

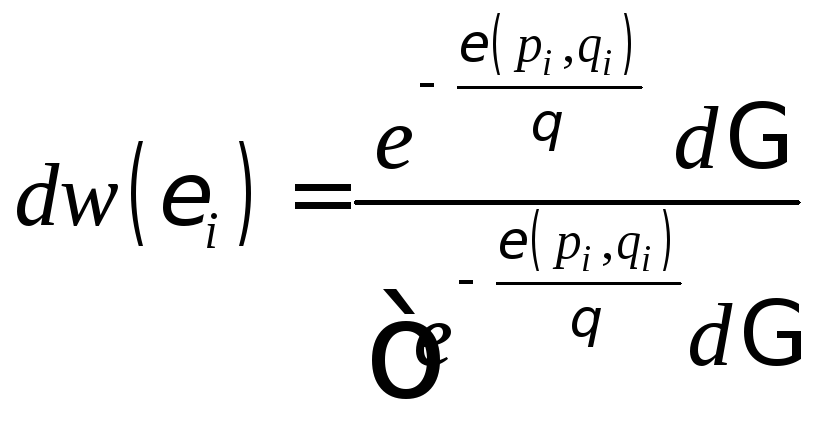, (1.9.14)

где – вероятность того, что микросостояние системы изображается одной из точек, находящихся в элементе фазового объёма, соответствующего интервалу энергий подсистемы отдо. Соответствующая функция распределения:

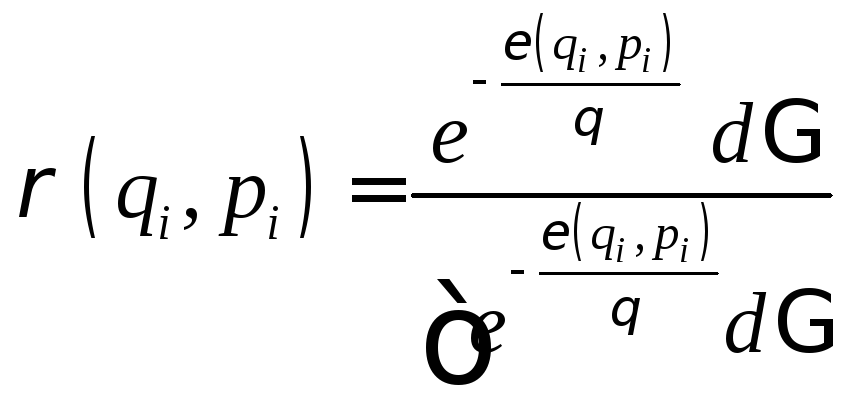, (1.9.15)

где – статистический интеграл.

в) Большое каноническое распределение Гиббса.

Подсистема обменивается с окружением (термостатом) не только энергией, но и частицами. Энергия подсистемы – , число частиц подсистемы –.Е и N – энергия и число частиц изолированной системы, состоящей из подсистемы и термостата. Распределение вероятностей называют большим каноническим распределением:

(1.9.16).

Из условия нормировки следует

. (1.9.17)

Физический смысл величины : она определяет вероятность того, что подсистема находится в одном из состоянийс энергиейи числом частицn. Буквой по-прежнему обозначена статистическая температура. Величина

(1.9.18)

(производная берётся при постоянном значении энергии) называется химическим потенциалом. Как и температура, химический потенциал может относится только к макроскопическим системам. Равенство химических потенциалов является условием равновесия макросистем, которые могут обмениваться между собой частицами. Физический смысл химического потенциала: он определяет изменение энергии системы при изменении числа частиц на единицу (при фиксированных энтропии и объёме).