Основи класифікації ланок.

Перехідний процес любої ланки може бути записаний в загальному випадку диференційним рівнянням.

В подальшому будемо передбачати, що диференційне рівняння ланки дано в безрозмірній формі.

В залежності від порядку рівняння ланок можуть бути нульового, першого, другого й більш високих порядків.

До простих відносяться ланки до 2 порядку. Класифікація простих ланок відбувається

або по диференційному операторувиходу ланки або по вигляду передатної функції

. Перша класифікація розглядає структуру ланки з точки зору його вільних

коливань без врахування збурюючих дій. Такий підхід може бути корисним при рішенні різних питань, що стосуються стійкості ланки. Друга класифікація по передатній функції більш поглиблена, вона точніше враховує характерні особливості ланки. Якщо притримуватися другої нормалізованої форми диференціального рівняння, то

класифікація по вихідному оператору може бути обмежена 12 видами полінома;

тобто:

Ланки оператори які мають додатний вільний член, рівний одиниці, називають статичним. Якщо вільний член відсутній, ланка називається остаточною.

Ланки оператори яких мають від'ємний вільний член, рівний одиниці, класифікуються як володіючі від'ємним статизмом.

Ланка з вихідним оператором типуназивається одноємнісною так як

одноємнісні елементи мають завжди рівняння типу. Ланка з оператором

є нестійкою, тому що єдиний корінь характеристичного рівняння завжди додатній, що як було сказано раніше приводить до нестійкого руху ланки.

Ланка, що має оператора, носить назву коливальної при умові, що

При ланка може бути розложеною на дві послідовно з'єднаних

ланки типутобто на дві одноємостних ланки.

, називають консервативною. Особливості цієї ланки

Ланка з оператором, називають консервативною. Особливості цієї ланки

полягають в тому, що вона створює при збурюючих діях нестихаючі коливання, тому що

обидва кореня характеристичного рівнянняє чисто уявними числами.

Ланки з оператором Р є інтегруючою, що витікає з рівняння

. Особливість цієї ланки є її властивість давати реакцію на

виході пропорційну значенню інтеграла від вхідної функції. Сигнал отриманий на виході ланки при подачі на його вхід одиничного імпульсу, називається ваговою, або

імпульсною, перехідною функцією. В цьому випадку зображення по Лапласу

вхідного сигналу, а зображення вихідного сигналу співпадає з передатною

функцією.

Переходимо від зображення до оригіналу і отримуємо вагову функцію.

тобто вагова функція є оригіналом передатної функції. Так як зображення вагової функціївідрізняється зображення передатної функціїтільки множником Р,

то

Таким чином, перехідну функцію завжди можна знайти вагову функцію;

• перехідна -

• вагова -

Ланка з операторомможе бути розкладена на дві послідовно з'єднані інтегруючіланки. Ланка, яка має оператор, може бути представлена як послідовна

комбінація з двох ланок:детобто як послідовне з'єднання

остаточної та одноємнісної ланок.

Перейдемо тепер до класифікації по передатній функції.

від, матимемо "сімейство" векторів. Криву, проведену через кінці радіусів -

векторів на комплексній площині, називають амплітудою — фазовою частотною характеристикою (АФЧХ).

АФЧХ характеризує зміну амплітуди коливань вихідної величини і зсуву фаз між вихідними та вхідними сигналами від частоти при незмінній амплітуді вхідного гармонійного діяння.

Залежність зміни амплітуди вихідного сигналу від частоти показуєі

фазочастотноюхарактеристиками. Підставимо у вихідне диференційне рівняння

значення вихідної і вхідної величин і візьмемо похідну за часом:

Поділимо добуте рівняння на_, винесемо за дужки спільні члени і з урахуванням

запишемо

порівнюючи з попередніми виразами, або виглядами цієї величини

визначимо, що математичний вираз для комплексного коефіцієнта передачі можна добувати, коли підставитизамість оператора Р у формулу передатної функції.

Підставимо у рівняння ізамість Р, позбавимося у виразі

комплексності в знаменнику та відокремимо дійсну та уявну частини.

Обидва додатки залежать від частоти і є окремими характеристиками, які будують при зміні частоти від. Вираз який не має уявності називають дійсною частотою

характеристики.

> а додаток у якому є- уявною (мнимою) частотною характеристикою.

Підставляючи значення частоти від 0 доу виразиможна побудувати

дійсну та уявну характеристики у функції частоти.

За парами значень Р і Q для окремих частот можна побудувати на комплексній площині амплітудно - фазову характеристику.

АФЧХ можна побудувати також за значеннями

Амплітудна частотна характеристика.

Фазова частотна характеристика:

Лекція №3. Вираз, який не має уявності, називають дійсною частотною характеристикою.

а додаток у якому є комплексна величина^— уявною частотною характеристикою.

змінюючи (^_ частоту) від 0 доможна побудуватидійсну й уявну характеристики і функції частоти. За парами значень P,Q для окремих частот можна побудувати на комплексній площині амплітудно-фазову частотну характеристику.

Амплітудна частотна характеристика, яка випливає з рисунку;

Фазова частотна характеристика;

Використовуючи рівняннядістанемо;

Прологарифмуємо вираз:

, за виразом

будуємо відповідно логарифмічну амплітуду (ЛАЧХ) і фазову (ЛФЧХ) частотні характеристики, які істотно спрощують дослідження систем автоматичного регулювання, їх будують із застосуванням зручніших на практиці десяткових логарифмів.

По шкалі частот замістьвідкладають. Логарифмічна шкала відносно

частотинерівномірна, а відносно- рівномірна.

Основними одиницями логарифмічної шкали є декада і октава.

Використовуючи рівняння, дістанемо:

Якщо прологарифмувати отримаємо

За виразамибудуть відповідно логарифмічною амплітудою, тобто ЛАЧХ

і логарифмічно — фазовою, а отже АФЧХ частотними характеристиками.

Октава-це інтервал частот між якимсь значенням частоти і її подвоєним значенням. Отже, октава зображується відрізком, що має однакову довжину на будь-якій ділянці

шкали. Довжина відрізка дорівнює

Декада-інтервал частот між певним значенням частоти та її значенням, збільшеним у 10 разів. Зображується декада відрізком завдовжки, це відрізок одиничної довжини,

оскільки

По осі ординат відкладають не, а пропорційну йому величину

, яку вимірюють у децибелах.

1 Децибел (дБ)- це 0.1Б (бел)- одиниці логарифмічної величини, що являє собою логарифм безрозмірного відношення фізичної величини до однойменної фізичної величини, яку вважають вихідною.

Змінна відношення двох величин у 10 разів відповідає зміні підсилення на 20дБ.

Враховуючи, щоє відношенням амплітуди коливань на вході виході, змінна

підсилення на 20дБ відповідає змінні відношення двох амплітуд у 10 разів. При відношенні двох величин, що дорівнюють 1, підсилення в децибелах дорівнює 0,

оскільки

Якщо відношення вихідного і вхідного коливань менше 1, підсилення в логарифмічному масштабі буде негативним, що означає ослаблення сигналу на виході порівняно зі входом.

При побудові логарифмічних фазових частотних характеристик по осі ординат відкладають значення кутів у натуральній величині, а по осі абсцис частотупо логарифмічній шкалі.

Прологарифмуємо вираз і дістанемо логарифмічну амплітудну частотну характеристику ЛАЧХ.

Логарифмічну характеристикубудують починаючи з

ЛАЧХ.

частоти розміщуються по мірі їх

можливості

Передатна функціяможе бути представлена у вигляді відношення у якої

чисельник і знаменник розкладені на множники з поліномів першого або другого ступеню в залежності з яких ланок складена досліджуємо модель системи. Звідси витікає, що побудова фазових і амплітудних характеристик може бути виконана шляхом побудови відповідних характеристик окремих ланок з наступним їх додаванням приймаючи до уваги їх знак (- або +).

Передатна функція - це алгебраїчний вираз. Використання W _(р) полегшає дії при

математичному описанні систем автоматичного керування. Дуже часто доводицШ* розглядати елементи і системи при дії на їх вході синусоїдальних сигналів.

Залежність вихідної величини від вхідної величини, що змінюється за синусоїдою,

характеризується комплексним коефіцієнтом передачі Wелемента або системе. Нехай на вході лінійного елемента діє сигнал.

де А₁ - амплітуда; ^— частота.

Після завершення перехідного процесу при кожному значенні частоти вихідна величина також робитиме синусоїдні коливання з частотоюале, як правило, з іншоюамплітудою А₂ і фазою . Тому вихідна величина;

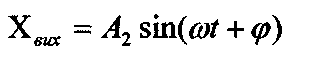
Зобразимо вихідну і вхідну величини у векторній формі:

Внаслідок зміни підсилювальних властивостей елементів на різних частотах амплітуда А₂ різниця фазє функціями частоти, і рівняння (2) запишемо у вигляді;

W

Для кожного значення частоти вхідного сигналу Wє вектор довжиною А, повернутим відносно позитивного напряму осі абсцис на кутЗмінивши частоту