книги по релейке часть 1 / ТОЭ / Демирчян К.С. Нейман Л. Р. Теоретические основы электротехники / Теоретические основы электротехники том 2

Глава 14. Цепные схемы. Электрические фильтры. Структурные схемы

203

Как видно из этих рисунков, характеристические сопротивления Zc ï m è Zc ò m близки к R0 в более широком диапазоне частот, чем Zc ï è Zc ò. Из рис. 14.14 видно, что для меньших значений m частота близка к ñ и рост затухания происходит более резко. Однако выбор слишком малых значений m связан со зна- чительным снижением затухания в полосе задерживания при больших , что нежелательно. По этой причине фильтры типа m обычно соединяют каскадно с фильтрами типа k, достигая тем самым желаемого коэффициента затухания в полосе задерживания при высоких частотах и большой крутизны роста ( ) около частоты среза. То обстоятельство, что фильтр типа m обладает характеристическим сопротивлением или Zc ï, èëè Zc ò, является очень полезным при согласовании звеньев типа k è m в многозвенном фильтре.

Порядок расчета фильтра можно принять, например, следующим: по сопротивлению нагрузки R0 и частоте среза ñ определяем исходные данные L0 è C0 для Г-образного прототипа по формулам

L			L1		R0	è C			C2		1	.
	0						0
		2			c			2			R0 c

Затем по формуле для th Г (см. § 14.3) находим коэффициент затухания звена. По желаемому значению коэффициента затухания всего фильтра при высоких частотах определяем число звеньев в фильтре. По желаемой крутизне роста ( ) находим и, следовательно, параметры фильтра типа m.

Конечно, приведенная схема расчета является весьма приближенной, так как точный расчет фильтра связан с учетом влияния рассогласования, наличия активных сопротивлений в элементах фильтра и т. д. Поэтому после проведения приближенного расчета следует, если необходимо, произвести уточнение с уче- том этих факторов. Для практических расчетов разработан ряд рекомендаций

èполучены серии кривых, которые дают возможность относительно просто

èточно спроектировать фильтр с желаемыми характеристиками.

14.6. Метод преобразования частоты. Электрические фильтры верхних частот. Полосовые электрические фильтры

Фильтры нижних частот могут служить основой для расчета фильтров верхних частот и полосовых фильтров. Для этой цели применим метод преобразования частоты. Он заключается в том, что если имеется некоторая функция F(p) комплексной частоты p, то можно получить другую функцию F(s) комплексной частоты s, пользуясь связью ð(s) между этими частотами.

Пусть исследуемой функцией является операторное сопротивление Z(p). Для цепи любой сложности Z(p) зависит от сопротивлений в ветвях, имеющих в общем случае вид Zi(p) pLi + 1/(pCi) + ri. Рассмотрим случай, когда r 0, т. е. когда цепь состоит из реактивных элементов. Преобразование частоты p(s) для таких цепей можно представить так, что в первоначальной цепи каждое сопротивление Zi(p) pLi + 1/(pCi) заменяется некоторым другим сопротивлением Zi(s) сложной конфигурации, определяемой видом функции p(s). Пусть p(s) a/s; тогда легко заметить, что в новых переменных Z i (s) aL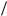s s(aCi ) 1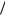(sCi ) sLi ,

Ðèñ. 14.15

204 Часть 2. Теория линейных электрических цепей

т. е. для переменной s можно получить новую цепь с сопротивлением Zi(s) из прежней цепи с сопротивлением Zi(p), заменив в последней все индуктивно-

ñòè Li на емкости Ci и все емкости Ci на индуктивности Li . Применительно к схеме Г-образного звена фильтра нижних час-

òîò (ðèñ. 14.15, à) преобразование p a/s дает схему, приведенную на рис. 14.15, á. Нетрудно видеть, что для этой схемы частотные зависимости сопротивлений холостого хода и короткого замыкания

Z10(s) jx10(s) è Z1ê(s) jx1ê(s) таковы, что полоса пропускания начи- нается с частоты c , т. е. фильтр с такой схемой пропускает только

высокие частоты (рис. 14.16 и 14.17).

Таким образом, фильтр верхних частот можно получить из фильтра нижних частот, заменив в последнем все емкости на индуктивности и все индуктивности на емкости (см. рис. 14.15). Если взять частоту среза одинаковой для обоих

фильтров ( c c ), то параметры фильтра верхних частот определятся через па-
раметры фильтра нижних частот равенствами C	C	0	è L	L	0	с указанной за-
0			0

меной мест элементов в схеме рис. 14.15. Характеристические параметры при этом запишутся в виде

Z c ï

R0

R0

;

1 Z1 (4Z 2 )

1 c2 2

R

R

1 2

2 ;

Z

c ò

0

1 Z

1

(4Z

2

)

0

c

	th Ρ		Z	1ê				1 ( j C )
								0
			Z	10				1 ( j C ) j L
								0	0

		1	.
	1	2 2
		c

Для получения характеристик полосового фильтра будем пользоваться методом преобразования частоты. Пусть p(s) bs + a/s. Тогда

1

a

1

Z(p) pL

bs

L

(bs a s)C

pC

s

Ðèñ. 14.16

bsL

1

1

.

1

s

aC

bsC

aL

s

Применение данного преобразования превращает индуктивность с сопротивлением pL в последовательно соединенные индуктивность и емкость с сопротивлением bsL + 1/(sC ), а емкость с проводимостью pC — в параллельно соединенные емкость и индуктивность с проводимостью bsC + aC/s (ðèñ. 14.18, à, á).

Рассмотрим, каким образом изменяется полоса пропускания фильтра нижних частот при использовании такого преобразования. Применяя соответствие p bs + a/s

Ðèñ. 14.17

Глава 14.

Цепные схемы. Электрические фильтры. Структурные схемы 205

и частотную характеристику передаточной функции Г-образ-

ного звена фильтра нижних частот (рис. 14.19), получим соот-

ветствия:

ïðè

s 0

p è U 2

U1

0;

ïðè

s

p è U 2

U1

0;

ïðè

s 2

a

p 0

è U

U

1.

b

2

1

Полагая комплексные частоты мнимыми: p j è s j ,

Ðèñ. 14.18

получим преобразование частотной характеристики передаточ-

ной функции. Частотам среза ñ фильтра нижних частот соот-

ветствуют две положительные частоты

è

(ðèñ. 14.19)

1c

2c

среза полосового фильтра, определяемые из уравнения

j

j b

a

èëè

b

a

.

j

c

c

Отсюда

c2

a

c

2c;1c

4b2

b

2b

èëè

Ðèñ. 14.19

c

b è

a b 2

,

2c

1c

1c

2c

Ι

причем частота

, ò. å. s2 – a/b соответствует p 0.

a b

0

Таким образом, если задана полоса пропускания полосового фильтра, лежа-

щая между частотами среза	è	, то легко рассчитать коэффициенты a è b
1c	2c

и тем самым параметры элементов преобразованной схемы, исходя из предварительно рассчитанного фильтра нижних частот типа k с заданной произвольно ñ при известном R0. Расчет сильно упрощается, если ширину полос пропускания полосового фильтра и фильтра нижних частот взять одинаковой, т. е.

			0	0.	Тогда b 1 è a	.
2c	1c				1c 2c

Метод преобразования частоты можно применить и по отношению к фильтрам типа m, получив таким образом фильтры типа m для верхних частот и соответствующие полосовые фильтры.

Если преобразование вида p bs + a/s применить по отношению к фильтру верхних частот, то можно получить также и заграждающий фильтр.

В качестве полосового фильтра могут служить и индуктивно-связанные контуры, содержащие конденсаторы, что видно из изложенного в § 6.8.

14.7. Структурные схемы

Сложность современных систем и устройств автоматики, радиотехники и электроизмерительной техники заставляет при анализе этих систем рассматривать укрупненно отдельные их участки и изучать в обобщенном виде свойства этих участков в отношении передачи через них сигналов и энергии. Эти свойства характеризуются передаточной функцией рассматриваемого участка системы.

206 Часть 2. Теория линейных электрических цепей

Такие отдельные участки системы, содержащие в себе в общем случае комплексы элементов, соединенных в сложные электрические цепи, называют иногда б л о к а м и системы.

При рассмотрении передаточных функций четырехполюсников, представляющих собой как раз один из наиболее распространенных видов укрупненного блока электрической цепи, можно заметить, что эта функция в значительной степени зависит от значений сопротивлений, подключаемых к входу и выходу четырехполюсника. Однако если все блоки системы согласованы между собой, а также с сопротивлениями источника энергии и приемника, то каждый блок характеризуется одной определенной передаточной функцией. Согласование может быть осуществлено не только подбором свойств самих блоков, но и путем включения между ними тех или иных дополнительных элементов, например трансформаторов с характеристиками, близкими к идеальным, обладающих свойством преобразовывать значение сопротивления (см. § 5.19). При соблюдении этих условий блоки системы характеризуются определенными передаточ- ными функциями.

Во многих случаях блоки системы характеризуются свойством односторонней направленности передачи сигнала или энергии от входных зажимов к выходным. Таковым является, например, транзисторный усилитель, в котором сигнал передается от входных зажимов базы к выходным зажимам коллекторной цепи, и передача сигнала в обратном направлении не происходит. Таковыми являются также различные блоки систем автоматики, в которых осуществляется воздействие только со стороны цепи управления на управляемую цепь. Подобные блоки называют б л о к а м и н а п р а в л е н н о г о д е й с т в и я.

Система, составленная из блоков направленного действия, условно изображается ее с т р у к т у р н о й с х е м о й. Каждый блок в этой схеме изображается в виде прямоугольника, внутри которого указывается его передаточная функция. Блоки соединяются между собой линиями со стрелками, указывающими направление передачи действия. Рядом с этими линиями помечаются величины, для которых определяется передаточная функция. Например, передаточные функции четырехполюсника могут быть определены как отношение операторных изображений, либо напряжений на выходе и входе, либо токов на выходе и входе, либо напряжения на выходе и тока на входе и, наконец, либо тока на выходе и напряжения на входе. Величины, операторные изображения которых входят в передаточную функцию, обозначаются на соединительных линиях между

блоками.

Рассмотрим несколько простейших способов

соединения блоков в структурных схемах.

Ðèñ. 14.20

Последовательное соединение в структурной

схеме указано на рис. 14.20.

Передаточная функция при этом в общем виде имеет выражение

X n (p)

X1(p)X 2 (p)X

3 (p)

X n (p)

n

K(p)

K

(p)K

(p) K

(p) K

(p).

1

2

n

j

X 0 (p) X 0 (p)X1(p)X

2 (p)

X n 1(p)

j 1

Глава 14. Цепные схемы. Электрические фильтры. Структурные схемы

207

Параллельное соединение в структурной схеме имеет некоторые особенности, связанные с направлением передачи действия. В этом смысле необходимо отли- чать в структурных схемах два вида узлов (точек), где происходит соединение нескольких блоков. На структурной схеме могут быть точки, где данная функция передается другим блокам без изменения. Назовем эти точки т о ч к а м и о т в е т в л е н и я. На структурной схеме их изображают в виде сплошных кружков. В другом случае в данной точке происходит суммирование или вычитание различных функций. Назовем эти точки т о ч к а м и с у м м и р о в а н и я (сложения). Такие точки на структурной схеме обозначают либо в виде кружков с крестиком (рис. 14.21), либо в виде, показанном на рис. 14.22.

Ðèñ. 14.21

Ðèñ. 14.22

Ðèñ. 14.23

Соединение, когда все входы блоков соединены в точке ответвления, а все выходы — в точке суммирования, называется п а р а л л е л ь н ы м с о е д и н е - н и е м в с т р у к т у р н о й с х е м е (рис. 14.23). При этом передаточная функция всей схемы определится как сумма передаточных функций отдельных блоков:

K(p) X(p) X 0 (p)

n

X j (p)

j 1

X 0 (p)

n

K j (p).

j 1

Схему, в которой входы двух блоков с различными направленностями соединены в точке суммирования, а их выходы — в точке ответвления, называют с х е - м о й с о б р а т н о й с в я з ь ю, такое соединение — а н т и п а р а л л е л ь н ы м. Пример такого соединения приведен на рис. 14.21 и 14.22. Нетрудно увидеть, что передаточная функция для схемы с обратной связью определится в виде

X(p) K1(p)X1(p) K1(p)[X 0 (p) X 2 (p)] X 0 (p)K1(p) X(p)K 2 (p)K1(p), откуда

K(p)	X(p)		K1(p)	,
	X 0 (p)		1 K1(p)K 2 (p)

что соответствует выражению, приведенному в § 13.7.

Часть структурной схемы, в которой выходная функция при помощи обратной cвязи передается к началу этой части схемы, называют з а м к н у т о й. Часть структурной схемы, в которой обратная связь отсутствует, называют р а з о м к - н у т о й. Соответственно отличают передаточную функцию замкнутой системы îò передаточной функции разомкнутой системы.

208 Часть 2. Теория линейных электрических цепей

Ðèñ. 14.24

Передаточную функцию всей сложной структурной схемы можно определить путем последовательного нахождения передаточных функций отдельных участков при помощи полученных выше формул для различных соединений. Например, передаточную функцию K(p) K12(p) всей схемы, изображенной на рис. 14.24, можно найти, выполняя операции, указанные на этом рисунке.

14.8. К вопросу об устойчивости в электрических цепях

В линейных электрических цепях, содержащих источники энергии, при наличии обратных связей может возникнуть вопрос об устойчивости процесса â öåïè.

Под устойчивостью будем понимать следующее. Если под влиянием некоторого кратковременного (импульсного) возмущения x0(t) система выйдет из состояния равновесия, то процесс в системе устойчив, когда возникшее отклонение x(t) от состояния равновесия после окончания действия возмущения стремится к нулю или остается неизменным. Процесс в системе неустойчив, если это отклонение нарастает. Итак, пусть x0(t) является импульсной функцией, и, следовательно, ее операторное изображение есть постоянная величина, т. е. X0(p) A. Операторные изображения отклонения и возмущающей функции свя-

заны через передаточную функцию K(p) X(p) , откуда

X 0 (p)

			Q(p)	k n	ak
X(p) X		(p)K(p) AK(p) A				,
	0
			G(p)	k 1 p pk

ãäå p1, p2, ..., pn суть корни уравнения G(p) 0, т. е. являются полюсами передаточной функции и, следовательно, полюсами величины X(p). При этом имеем

Глава 14. Цепные схемы. Электрические фильтры. Структурные схемы 209
n	n
x(t) a epkt	a e Κk j k t .
k	k
k 1	k 1

Система устойчива, если вещественные части Κk всех корней pk отрицательны, так как x(t) 0 ïðè t . Система устойчива и в том случае, если пара сопряженных корней имеет Κk 0, так как при этом устанавливаются колебания с

	неизменной амплитудой. Система неустойчива,
	если хотя бы один из корней имеет положительную
	вещественную часть Κk > 0, так как соответству-
	þùèé ÷ëåí epkt будет неограниченно возрастать.
	Отсюда следует, что система устойчива, если все
	полюсы передаточной функции лежат в левой по-
	луплоскости переменной p Κ + j или на мнимой	Ðèñ. 14.25
	оси. Система неустойчива, если хотя бы один полюс

передаточной функции лежит в правой полуплоскости (рис. 14.25).

Пусть в рассматриваемой линейной системе полностью отсутствуют обратные связи и она устойчива, т. е. передаточная функция K1(p) этой разомкнутой системы не имеет полюсов в правой полуплоскости. Замкнем систему с помощью обратной связи, передаточная функция K2(p) которой также не имеет полюсов в правой полуплоскости.

Передаточная функция замкнутой системы имеет вид

K 3 (p)

K1(p)

Q1(p) G1(p)

1 K1(p) K

Q1(p)Q2 (p)

2 (p)

1

G1(p)G2 (p)

Q1(p)G2 (p)

Q1(p)G2 (p)

.

G (p)G

(p) Q

(p)Q

(p)

b pn b

pn 1

b

1

2

1

2

n

n 1

0

В знаменателе передаточной функции имеем разность двух полиномов от p

G1(p)G2(p) – Q1(p)Q2(p), и поэтому в результирующем полиноме bn p n + bn–1 p n–1 + + ... + b0 возможно появление корней в правой полуплоскости и система может

оказаться неустойчивой. По этой причине возникает необходимость в исследовании вопроса об устойчивости замкнутой системы, если даже заведомо известно, что разомкнутая система является устойчивой.

Для того чтобы система была устойчивой, коэффициенты полинома знаменателя должны удовлетворять определенным условиям, известным в литературе под названием критериев устойчивости Рауса–Гурвица. Приведем без доказательства эти критерии. Составим вспомогательную матрицу коэффициентов полинома bn p n + bn–1 p n–1 + ... + b0, состоящую из n строк и n столбцов, в следующем виде

Ðèñ. 14.26

Часть 2. Теория линейных электрических цепей

210

bn 1	bn	0	0	0		0
bn 3	bn 2	bn 1	bn	0		0
bn 5	bn 4	bn 3	bn 2	0		0	.
. . . . . . . . . . . . . . . . . . . . .
0	0	0	0		b1	b2
0	0	0	0		0	b0

По вертикали номера коэффициентов изменяются на две единицы, а по горизонтали идут по порядку. По виду матрицы очевиден способ ее построения. Гурвиц показал, что если все n диагональных миноров этой матрицы больше нуля, то полином не имеет корней в правой полуплоскости. Будем считать, что bn > 0. Тогда первый минор этой таблицы будет bn–1, второй минор есть определитель, составленный из членов двух первых строк-столбцов:

	1	b	8 0;		2		bn 1		bn	,
		n 1						bn 3	bn 2
третий минор
				bn 1		bn		0
		3		bn 3	bn 2			bn 1
				bn 5	bn 4			bn 3

и так далее.

Таким образом, критерием устойчивости служат неравенства

1 8 0; 2 8 0; 3 8 0; ; n 8 0.

При анализе систем с отрицательной обратной связью находят применение также частотные критерии устойчивости.

Рассмотрим один из таких критериев, основанный на анализе годографа ам- плитудно-фазовой частотной характеристики разомкнутой системы.

При разрыве цепи обратной связи в месте прохождения сигнала Õ2 (см. рис. 14.21) образуется разомкнутая система с двумя последовательно соединенными блоками с передаточной функцией

K(p) X 2 (p) K1(p) K 2 (p).

X 0 (p)

По виду годографа амплитудно-фазовой частотной характеристики K(j ) K1(j ) K2(j ) можно судить о том, будет ли устойчивой замкнутая система.

Если при 0 разомкнутая система имеет коэффициент передачи, при котором влияние высокочастотных помех минимальное, равный

K( j0) = Kó , à ïðè K( j ) 0, что характерно для систем управления и регулирования, то типичный годограф K( j ) имеет показанный на рис. 14.26 вид.

Глава 14. Цепные схемы. Электрические фильтры. Структурные схемы

211

Так как годограф проходит через четыре квадранта, то в рассматриваемом случае наивысшая степень полинома знаменателя передаточной функции K(p) превышает на четыре наивысшую степень полинома числителя (см. § 13.5).

При частоте 1, соответствующей точке пересечения годографа K(j ) с отрицательной частью оси вещественных, угол сдвига по фазе между сигналами Õ0 è Õ2 составляет 180Τ, так что, учитывая, что обратная связь отрицательная, при возникновении колебаний сигнала Õ0 с частотой 1 и замыкании цепи обратной связи сигнал Õ2 будет совпадать по фазе с сигналом Õ0.

В результате обратная связь при = 1 становится положительной и система может стать неустойчивой, что будет иметь место, если коэффициент передачи системы при частоте 1 превышает 1.

Вопросы упражнения и задачи к главам 13 и 14

13.1. Уравнения и системы параметров четырехполюсников

ВОПРОСЫ

1.Могут ли все параметры четырехполюсника быть: à) вещественными; á) мнимыми; â) комплексными?

2.В каких случаях целесообразно выбирать услов-

ные положительные направления токов I1, I 2 так, как указано на рис. B13.1 и B13.2?

	3. Сколько параметров четырехполюсника необхо-
	димо задать, чтобы записать уравнения, связываю-	Ðèñ. B13.1
	щие токи и напряжения на его входных и выход-
	ных зажимах, если известно, что четырехполюсник:
	à) симметричный, á) несимметричный?
	4. Могут ли параметры A, B, C, D пассивного четы-
	рехполюсника быть все равными единице?	Ðèñ. B13.2
	5. A-параметры четырехполюсника, содержащего ре-

активные элементы, рассчитаны при частоте напряжения 0. Сохранят ли они свои значения при частоте 2 0?

6.Почему Í-параметры четырехполюсника называют гибридными?

7.(О) Сколько можно предложить систем параметров пассивного четырехполюсника, связывающих его входные и выходные напряжения и токи?

УПРАЖНЕНИЯ

1. Выразите недостающий в строках – таблиц параметр четырехполюсника через заданные:

? B C D

? H12

H 21

H 22

? Z12

Z 21

Z 22

)

,

)

,

)

,

à) )A ? C D,

; á) )H11

?

H 21

H 22 ,

; â) )Z11

?

Z 21

Z 22 , .

)A B ? D,

)H11

H12

?

H 22

,

)Z11

Z12

?

Z 22

,

)

,

)

H12

H 21

?

,

)

Z12

Z 21

?

,

(A B C ? +

(H11

+

(Z11

+

2.Выразите через Z-параметры симметричного четырехполюсника его A-, Y- è H-параметры при указанных на рис. B13.1 и B13.2 положительных направлениях токов и напряжений.

3.(Р) Выразите параметры четырехполюсников, показанных на рис. B13.3, че- рез параметры r, L, C их элементов в установившемся синусоидальном режиме.

Могут ли быть определены: à) Z-параметры четырехполюсников в строке a; á) Y-параметры четырехполюсников в строке á?

ЗАДАЧИ

1. (Р) Найдите A-, Z-, Y-параметры изображенных на рис. B13.4 четырехполюсников.