книги по релейке часть 1 / ТОЭ / Демирчян К.С. Нейман Л. Р. Теоретические основы электротехники / Теоретические основы электротехники том 2

Вопросы упражнения и задачи к главам 13 и 14

223

9. (О) К чему приводит отклонение от линейной зависимости Π k коэффициента фазы при передаче сигнала через фильтр?

УПРАЖНЕНИЯ

1. Изобразите зависимость коэффициента затухания ( ) идеальных фильтров: à) нижних частот; á) верхних частот; â) полосового; ã) заграждающего от частоты .

2. (О) Получите выражения для характеристических параметров Zc1, Zc2, Ã + jΠ изображенных на рис. B14.6 фильтров, вычисляя предварительно их сопротивления в режимах холостого хода и короткого замыкания. Значения сопротивлений на схеме указаны в омах, индуктивностей — в миллигенри, емкостей конденсаторов — в микрофарадах, f 500 Ãö.

Ðèñ. B14.6

3. (О) Рассчитайте и постройте зависимости коэффициента затухания ( ) и коэффициента фазы Π( ) фильтров, схемы которых изображены на рис. В14.6, при условии их согласования с сопротивлениями источника и приемника при всех частотах. Cравните построенные зависимости ( ) с аналогичными, полу- ченными при питании фильтров от идеального источника ЭДС и сопротивлении приемника rïð 200 Îì.

4.(О) Найдите параметры Z1 è Z2 Г-образного фильтра, включенного между источником с внутренним сопротив-

лением Zè и приемником с сопротивлением Zïð и согласующего источник и приемник.

5.(Р) Получите выражения для амплитудно-частотной характеристики и постройте зависимость K( ) для изображенных на рис. В14.7 фильтров: à — нижних частот; á — верхних частот. Примите следующие параметры эле-

ментов: à)		r1 75 êÎì,	r2 3,94	êÎì,	Ñ1 10–7	Ô,
Ñ2	9,5·10–7	Ô, k 10; á)	r1 39,3	êÎì,	r2 717	Îì,
Ñ1	Ñ2 10–7 Ô, k 100.					Ðèñ. B14.7

224 Вопросы упражнения и задачи к главам 13 и 14

14.3. Электрические фильтры нижних частот типов k è m

	ВОПРОСЫ
	1. Можно ли построить фильтр верхних частот типа k?
	2. (О) К каким качественным изменениям зависимости
	( ) Г-звена, изображенной на рис. В14.8, приведет со-
	единение нескольких Г-звеньев, при условии согласова-
	ния их между собой, с источником и нагрузкой?
	3. Можно ли построить фильтр верхних частот типа m?
	4. (О) Одинакова ли полоса пропускания звена-прото-	Ðèñ. B14.8
	типа и производных от него звеньев?

5. (О) Какими положительными и отрицательными качествами характеризуется Г-образное звено фильтра нижних частот, содержащее как параллельный, так и последовательный LC-контуры одновременно?

6. Можно ли с помощью метода преобразования частоты построить фильтр нижних частот, имея схему фильтра верхних частот?

7. Можно ли применить метод преобразования частоты для получения фильтров, не принадлежащих к типам k è m?

8. (О) Как изменятся характеристики ( ), U 2 ( ) фильтров нижних и верхних U1( )

частот при преобразовании частоты в соответствие с формулой p(s) bs?

УПРАЖНЕНИЯ

1.(Р) Фильтр нижних частот типа k имеет параметры элементов L 0,1 10–3 Ãí,

C 64 10–8 Ф. Рассчитайте частоту среза ñ, а также зависимости Zñ ò( ), Zñ ï( ). Постройте зависимости ( ), Π Π( ) и найдите частоту, при которой: à) коэффициент затухания равен 3 дБ; á) коэффициент фазы Π равен #/4.

2.(Р) Рассчитайте параметры LC-фильтра нижних частот, нагруженного на при-

емник сопротивлением rïð 10 Ом и подключенного к источнику с внутренним сопротивлением rè 10 Ом. Частота среза фильтра ñ 103 c–1.

3.Рассчитайте частоты среза фильтров нижних частот, схемы которых изображены на рис. B14.6 (варианты á, â).

4.(Ð) LC-фильтр нижних частот (L 0,2 Ãí, C 0,2 мкФ) согласован с источником и приемником. На входе фильтра действует напряжение u(t) 2 sin 0,4 104t + + 2 sin 1,5 104t В. Рассчитайте напряжение на выходе фильтра.

5.Рассчитайте параметры последовательно-производного фильтра нижних час-

òîò òèïà m и необходимое число звеньев при заданных частоте среза ñ 10 c–1, сопротивлении приемника rïð 10 Ом, коэффициента затухания 20 дБ при

1,2 ñ.

Вопросы упражнения и задачи к главам 13 и 14

225

14.4. Электрические фильтры нижних частот
УПРАЖНЕНИЯ
1. (О) При максимально плоской аппроксимации характеристики K( ) U2/U1
идеального фильтра нижних частот используют функцию f ( )	1	, ãäå

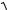1 Υ 2 12n

Υ — параметр, 1 / c, c — частота среза, n 1, 2, ... — порядок фильтра. Изобразите функцию f( ) ïðè Υ 0,5, Υ 1, n 1, n 2.

2. (Р) Рассчитайте значение параметра Υ, входящего в выражение аппроксими-

рующей функции f ( )	1	, при котором неравномерность коэффици-

1 Υ 2 2n

ента затухания фильтра низкой частоты в полосе пропускания не превысит зна- чения 3 дБ.

3.(Р) Заданная неравномерность коэффициента затухания фильтра нижних частот в полосе пропускания составляет 2 дБ. Найдите порядок фильтра при максимально плоской аппроксимации его характеристики K( ), при котором коэффициент затухания при частоте сигнала ; 2 ñ превышает 10 дБ.

4.(Р) Найдите соотношение между параметрами rC-фильтра нижних частот при максимально плоской аппроксимации его характеристики K( ) и неравномерности коэффициента затухания 3 дБ в полосе пропускания. Рас-

считайте значение коэффициента затухания при частоте сигнала 2 ñ (rïð ).

5. (Р) Найдите соотношение между параметрами r, L, C фильтра
нижних частот второго порядка (рис. B14.9) при максимально
плоской аппроксимации его характеристики K( ) и неравно-
мерности коэффициента затухания = 3 дБ в полосе пропус-
кания (rïð = ).	Ðèñ. B14.9

6. (О) Запишите амплитудные и фазовые частотные характеристики фильтров (см. упр. 5, §13.5, схемы вариантов á, â, ã, ä, å), используя полученные выражения для их передаточных функций.

14.5. Устойчивость в электрических цепях

ВОПРОСЫ И УПРАЖНЕНИЯ

1.(О) Может ли быть неустойчивой линейная à) пассивная электрическая цепь; á) электрическая цепь, не содержащая независимых источников; â) электриче- ская цепь с зависимыми источниками?

2.Может ли быть неустойчивой электрическая цепь, не содержащая реактивных элементов?

3.(Р) В цепи обратной связи усилителя с коэффициентом усиления K(p) k включено устройство с передаточной функцией W (p) 1(Tp 1). Может ли эта система быть неустойчивой (k > 0)?

226 Вопросы упражнения и задачи к главам 13 и 14

4. (Р) Усилитель с коэффициентом усиления k охвачен отрицательной обратной связью. Передаточная функция устройства обратной связи

à) W(p)		1		; á) W(p)		1		.
	a p2				a p3	a p2
		a p 1					a p 1
0			1		0	1	2

Может ли система быть неустойчивой? (a0, a1, a2 > 0)

5. (Р) Усилитель с передаточной функцией K k(Òð 1 Πk) неустойчив. Для стабилизации его охватывают отрицательной обратной связью, причем передаточная функция устройства обратной связи суть Wîñ (p) . При каких он будет устойчивым? (k > 0)

6.(Р) Используя выражение для передаточной функции, полу- ченное в упр. 5 § 13.5, найдите соотношение между параметрами электрической цепи (рис. В14.10), при выполнении которого цепь становится неустойчивой.

7.(О) Определите соотношение параметров элементов элек-

	трических цепей, изображенных на рис. В13.15, при котором це-	Ðèñ. B14.10
	пи устойчивы.

8. (Р) Характеристическое уравнение устойчивой системы имеет вид

b6 ð6 + b5 ð5 + b4 ð4 + b3 ð3 + b2 ð2 + b1 ð + b0 0. Устойчива ли система, характеристическое уравнение которой b0 ð6 + b1 ð5 + b2 ð4 + b3 ð3 + b4 ð2 + b5 ð + b6 0?

9. (Р) Устойчивы ли системы, характеристические уравнения которых имеют вид:

à) 3ð3 + ð2 + 2ð + 1 0; á) ð4 + ð3 + 3ð2 + 2ð + 1 0; â) ð4 + 3ð3 + 2ð + 1 0; ã) ð5 + 3ð4 + 2ð3 + ð2 + 4ð + 1 0; ä) ð5 + 3ð4 + 2ð3 + ð2 + 4ð 0; å) ð5 + 3ð4 + ð2 + 4ð + 1 0; æ) ð5 + 3ð4 + 3ð3 + 5ð2 + ð + 1 0; ç) 7ð7 + 6ð6 + 4ð5 + 5ð4 + ð3 + 2ð2 + 3ð – 1 0.

10. (Р) С помощью критерия Гурвица найдите соотношения между параметрами элементов и коэффициентом K усиления усилителя для схем (см. рис. В13.15), при которых цепи будут устойчивы.

Ðèñ. B14.11

Ðèñ. B14.12

Вопросы упражнения и задачи к главам 13 и 14

227

11. (О) На рис. В14.11 изображены годографы K(j ) амплитудно-фазовых частотных характеристик трех систем с разомкнутой цепью отрицательной обратной связи (передаточная функция разомкнутой системы суть K(ð) K0(ð)W(p), ãäå K0(ð), W(p) — передаточные функции основного устройства и устройства обратной связи). Какие из систем устойчивы при замыкании цепи обратной связи?

12. (О) На рис. В14.12 изображены логарифмические амплитудно-частотные и фазочастотные характеристики двух систем с разомкнутыми цепями единичной отрицательной обратной связи. Какая из систем устойчива при замыкании цепи обратной связи?

Глава пятнадцатая

Синтез электрических цепей

15.1. Задача синтеза электрических цепей

Все изложенное ранее относилось к анализу процессов в электрических цепях, т. е. к исследованию изменений во времени токов и напряжений в заданной электрической цепи. Однако исключительное значение имеет обратная задача — построить такую электрическую цепь, процессы в которой будут протекать по заданному закону. Решение подобных задач, обратных задаче анализа, носит наименование с и н т е з а э л е к т р и ч е с к и х ц е п е й.

Пусть ставится задача создать цепь с требуемыми характеристиками из линейных элементов. Входная величина (напряжение или ток) является заданной функцией времени x1(t). Ее операторное изображение X1(p), следовательно, также известно. Задан также и требуемый закон изменения во времени выходной величины x2(t) (напряжения или тока), и, соответственно, известно ее операторное изображение X2(p).

Таким образом, имеем выражение K(p) X2(p)/X1(p) для передаточной функции, которой должна обладать создаваемая электрическая цепь, преобразующая

x1(t) â x2(t).

Задача, следовательно, состоит в том, чтобы по заданному операторному выражению передаточной функции K(p) цепи или, соответственно, по заданной частотной характеристике K(j ) цепи построить конкретную цепь, обладающую такой характеристикой или хотя бы характеристикой, близкой к заданной.

Входные сопротивление или проводимость двухполюсника можно представить как частные случаи передаточной функции, если в качестве входной функции рассматривать одну из величин — ток или напряжение на входе, а в качестве выходной — другую из этих величин: напряжение или ток на входе. Нередко для общности и краткости входные и передаточные функции цепи называют просто ф у н к ц и я м и ц е п и и обозначают через F(p).

Функции цепи для линейных цепей с сосредоточенными параметрами являются рациональными дробями комплексной частоты p Κ + j . Их свойства, а следовательно, и свойства описываемых ими электрических цепей однозначно определяются распределением нулей и полюсов этих функций. Функции цепи могут быть представлены также в виде частотных характеристик.

При анализе электрических цепей мы видели, что различные электрические цепи могут иметь одинаковую по виду функцию цепи. Например, две различные цепи на рис. 13.13 являются дифференцирующими цепями и имеют одинаковый вид передаточной функции, а также две различные цепи на рис. 13.14 являются интегрирующими и обладают передаточными функциями одинакового вида. Уже отсюда видно, что одна и та же задача синтеза может иметь различные конкретные решения, т. е. решение ее неоднозначное.

В некоторых случаях, наоборот, конкретное решение задачи синтеза с помощью линейных пассивных цепей может отсутствовать, например, если для реа-

Глава 15. Синтез электрических цепей

229

лизации заданной функции требуется иметь в цепи отрицательное активное сопротивление.

В связи с этим возникают следующие основные вопросы синтеза цепи по заданной функции цепи F(p).

Первым вопросом является выяснение возможности физической реализации цепи, соответствующей заданной функции F(p), с помощью обычных элементов — конденсаторов, катушек, резисторов.

Если функция задана графически в виде частотной характеристики или явной функции времени, то в связи с этим вопросом возникает задача ее аналити- ческой аппроксимации таким образом, чтобы физическая реализация цепи была возможной.

Вторым вопросом синтеза является разработка метода конкретной реализации заданной функции сначала в виде схемы цепи, а затем и в виде физической электрической цепи. При этом важным представляется выбор рационального пути реализации ввиду указанной ранее многозначности решения задачи; в ча- стности, оказываются возможными эквивалентные преобразования схемы цепи с целью уменьшения числа ее элементов.

Для выработки требований, предъявляемых к функции F(p) в отношении ее реализуемости при помощи пассивных элементов электрических цепей, рассмотрим в следующем параграфе некоторые свойства входных функций Z(p) è Y(p) электрических цепей.

15.2. Свойства входных функций пассивных электрических цепей

В настоящем и в четырех последующих параграфах будем рассматривать входные операторные и комплексные сопротивления и проводимости, т. е. входные функции двухполюсников, так как для них можно наиболее легко уяснить условие физической реализации заданной функции F(p) с целью синтеза двухполюсников. В последнем параграфе главы рассмотрим более сложный вопрос — о синтезе четырехполюсников по заданной передаточной функции.

Сформулируем основные свойства входных функций пассивных электриче- ских цепей, установленные или же вытекающие из рассмотренного ранее.

Первым свойством входных операторных сопротивлений Z(p) и проводимостей Y(p) пассивных электрических цепей является то, что они будут вещественными при вещественных значениях p (p Κ). Действительно, коэффициенты полиномов от p в числителе и знаменателе величин Z(p) è Y(p) являются вещественными, так как они образуются суммами, разностями, произведениями и ча- стными от деления вещественных параметров R, L, C участков цепи. Поэтому при p вещественном Z(p) è Y(p) будут вещественными.

Второе свойство величин Z(p) è Y(p), отмеченное в § 10.6, заключается в том, что их полюсы и нули располагаются только в левой полуплоскости комплексного оператора p Κ + j (комплексной частоты) или на оси мнимых, т. е. Κk 0, причем в случае Κk 0 полюсы и нули простые. При этом все коэффициенты полиномов от p, стоящих в числителе и в знаменателе рациональных дробей, выра-

Ðèñ. 15.1

230 Часть 2. Теория линейных электрических цепей

жающих Z(p) è Y(p), положительны. Действительно, разложив полином на множители:

a pn a

pn 1

a

0

a

(p p

n

)(p p

n 1

) (p p ),

n

n 1

n

1

будем иметь для

каждой

ïàðû

сопряженных

комплексных

корней pk è

*

произведения множителей вида

pk 1 pk

(p – pk )(p – p* k ) (p – Κk – j k)(p – Κk + j k) (p – Κk)2 + 2k

и для вещественных корней pi множители вида p – pi p – Κi. Отсюда видно, что если все Κk 0 è Κi 0, то множители, на которые разложен полином, не содержат отрицательных чисел и, следовательно, все коэффициенты an, an–1, ..., a0 полинома положительны.

Третьим важным свойством рассматриваемых функций является то, что их вещественная часть положительна или равна нулю: Re [Z(p)] ; 0 è Re [Y(p)] ; 0, т. е. не отрицательна при условии, что Κ ; 0. Действительно, пусть Κ 0, ò. å. p j . В этом случае Z(j ) è Y(j ), как было указано в § 10.3, являются обычными комплексными сопротивлением и проводимостью. При наличии отличающегося от нуля положительного активного сопротивления хотя бы в одной ветви двухполюсника активная мощность на входе двухполюсника положительна и, следовательно, активное сопротивление и активная проводимость всего двухполюсника также положительны, т. е. Re [Z(j )] > 0. Когда в цепи имеются только реактивные элементы, то Re [Z(j )] 0. Покажем теперь, что Re [Z(p)] > 0 даже для чисто реактивной цепи, если Κ > 0. Например, для цепи на рис. 15.1, à имеем в этом случае выражение для операторного сопротивления:

Z(p) pL	1	(Κ j )L	1	ΚL j L	1	.
	pC		(Κ j )C
					ΚC j C

Это выражение по форме полностью совпадает с выражением для комплексного сопротивления Z(j r + j L + 1/(g + j C) цепи, изображенной на рис. 15.1, á. Последнее при r > 0 è g > 0 имеет вещественную часть больше нуля, точно так же

èвещественная часть операторного сопротивления Z(p) öåïè íà ðèñ. 15.1, à ïðè

Κ> 0 больше нуля. Для любой сложной цепи, состоящей только из реактивных элементов, аналогично может быть построена цепь, содержащая активные элементы, причем последовательно с каждой катушкой Li добавляется сопро-

тивление ri ΚLi и параллельно каждому конденсатору Ci добавляется проводимость gi ΚCi. При этом операторное входное сопротивление Z(p) реактивной цепи при

p Κ + j è Κ > 0 будет по форме совершенно аналогичным комплексному сопротивлению Z(j ) всей цепи с добавленными активными элементами. Активное сопротивление последней цепи r Re [Z(j )] больше нуля из физических соображений, так как для нее активная мощность положительна. Следовательно, и Re [Z(p)] > 0 ïðè Κ > 0 для реактивной цепи. Это условие и подавно имеет место для цепи, содержащей активные сопротивления и проводимости.

Глава 15. Синтез электрических цепей

231

Функции, обладающие указанными выше свойствами, называют п о л о ж и - т е л ь н ы м и в е щ е с т в е н н ы м и ф у н к ц и я м и.

Из изложенного вытекает, что для того чтобы рациональная дробь

F(p)	a pn a	pn 1 a			G(p)
	n	n 1	0
	b pm b		pm 1 b		Q(p)
	m	m 1	0

представляла собой операторное выражение входной функции и могла быть реализована в виде конкретной электрической цепи, она должна удовлетворять перечисленным требованиям, т. е. числитель и знаменатель должны иметь нули в левой полуплоскости или на оси мнимых, все коэффициенты ak è bk должны быть вещественными и положительными и, наконец, должно быть Re [F(p)] ; 0 ïðè Re (p) Κ ; 0.

Кроме того, в соответствии с изложенным в § 6.6 степени n è m полиномов числителя и знаменателя не должны отличаться друг от друга более чем на единицу.

15.3. Представление входных функций в виде простых дробей

Входную функцию F(p), являющуюся рациональной дробью, можно представить в виде суммы двучлена A p + A0 и простых дробей:

F(p)	G(p)	A p A0	A1		A2		Am	,
	Q(p)		p p1		p p2
							p pm

ãäå p1, p2, ..., pm — корни знаменателя Q(p). Ïðè ýòîì A 0, если степень n числителя на единицу больше степени m знаменателя. Случай A 0 è A0 0 имеет место, если n m. Когда n m – 1, коэффициенты A 0 è A0 0. Индекс у первого коэффициента A имеет тот смысл, что этот коэффициент при n m + 1 определяется из выражения для F(p), приведенного в конце предыдущего пара-

графа в виде A

F(p)

an

. Коэффициенты A1, ..., Am определяются после

p

p

bm

выделения двучлена A p + A0 по способу, изложенному в § 10.5.

Рассмотрим частный случай, когда корни знаменателя Q(p) либо мнимые,

либо вещественные.

Мнимые корни должны быть попарно сопряженными. Пусть, например,

p

k

j

k

è p

k+1

–j

. Ïðè ýòîì A

k

A

jA

è A

k 1

должны быть сопряженными

k

*

k

k

величинами, т. е. A

A

jA . Объединяя соответствующую пару про-

k 1

A

k

k

k

стых дробей, получаем

Ak

Ak 1

*

Ak (p j k ) Ak (p j k )

p pk

p pk 1

(p j k )(p j k )

(A

*

)p (A

*

) j

2A p

2A

k

A

k

k

A

k

k

k

k

k

.

p2 2

p2

2

p2 2

k

k

k

Убедимся, что если соблюдено условие Re [F(p)] ; 0 ïðè Κ ; 0, òî A 0.

k

Пусть p Κ 0, тогда из этого условия следует, что (–2A /

) ; 0 и, следова-

k

k

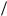232 Часть 2. Теория линейных электрических цепей

тельно, A 0. Пусть теперь p j è >							, ò. å. p2	+ 2	– 2 + 2	< 0. Тогда из
k						k		k	k
		2A
того же условия следует, что				k k		; 0, ò. å. A ; 0. Оба неравенства для
			2	2
								k
				k

A удовлетворяются одновременно только при A 0. Учитывая это, имеем

k

k

A

k

A

k 1

2A p

B

k

p

k

,

p pk

p pk 1

p2 k2

p2 k2

ãäå B

k

2A

2A

k

— вещественное число.

k

Если корень pi

Κi –−i вещественный, то соответствующая ему простая

дробь имеет вид

Ai

Ai

.

p pi

p

− i

Таким образом, разложение функции F(p) при наличии только вещественных

и мнимых корней можно записать в виде

F(p)

G(p)

A p A0

B1 p

B3 p

Am 1

Am

. (*)

Q(p)

p2 2

p2 2

p

−

m 1

p −

m

1

3

15.4. Реализация входных функций двухполюсника, имеющих вещественные и мнимые корни знаменателя, при помощи разложения этих функций на простые дроби

Пусть все коэффициенты в разложении (*) функции F(p) вещественны и положительны. Рассмотрим, как могут быть реализованы отдельные члены этого разложения. Предположим, что функция F(p) должна выражать входное операторное сопротивление цепи, т. е. F(p) Z(p).

Первое слагаемое A p Z (p) реализуется с помощью катушки с индуктивно-
ñòüþ L A , так как операторное сопротивление для нее равно L p.
Второе слагаемое A0 Z0(p) реализуется с помощью участка с активным со-
противлением r0 A0.
Слагаемое, имеющее вид	Bk p				1				, реализуется с помощью
	p2 2		p B	k	2	(pB	k	)
	k				k

участка цепи, состоящего из параллельно соединенных конденсатора с емкостью

Ck и катушки с индуктивностью Lk (рис. 15.2). Действительно, операторное со-
противление такого участка имеет вид Zk(p)		1		, и, следовательно,
		1
	pCk		(pLk )

выбрав Ck 1/Bk è Lk Bk/ 2k , осуществим требуемую реализацию.

Ðèñ. 15.2

Ðèñ. 15.3

Ðèñ. 15.4