Загальна фізика / Теоретичні курси / Конспект лекцій з фізики №1

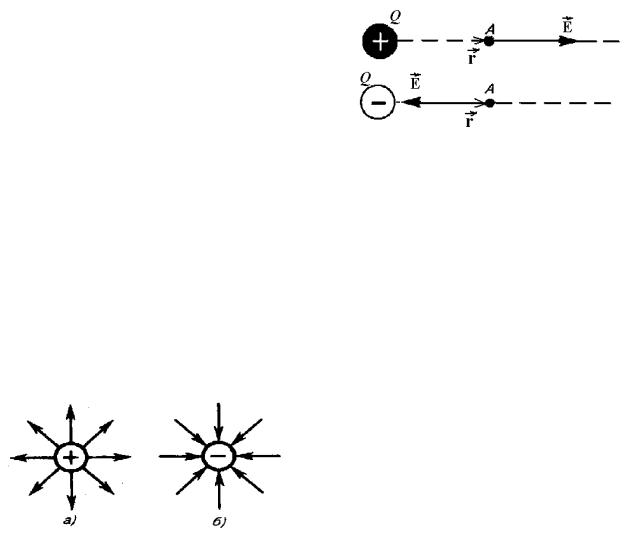
Напрям сили Кулона (рис. 37) визначається згiдно з експериментальними властивостями поведiнки електричних зарядiв. Тому закон Кулона можна сформулювати у векторному виглядi

	→	Q1 Q2	→	(208)
	Fq= k		r .
		r3

3.1.3 Електростатичне поле, напруженiсть електростатичного поля

Напруженiсть електростатичного поля в

→

данiй тоцi поля це вектор E, напрям якого спiвпадає з напрямом дiї сили Кулона, яка дiє на пробний додатнiй точковий заряд, розташований у данiй точцi поля, з боку електорстатичного поля

	→		→
		=	F	.	(209)
	E
			Q
				0

Якщо електростатичне (електричне) поле утворюється довiльним точковим зарядом Q (рис. 37), то модуль вектора напруженостi поля на вiдстанi r згiдно з законом Кулона є

Рис. № 38:

	E = F/Q0 = k	Q Q0	= k	Q	. (210)
		Q0 r2		r2

→

Модуль вектора E не залежить вiд величини пробного заряду Q0.

→ У векторному виглядi напруженiсть

E електростатичного поля, яка утворюється точковим зарядом Q, є

	→		→		→
		=	F	= k	Q r		.	(211)
	E
			Q0		r3

Графiчно електростатичне поле вiдтворюють за допомогою лiнiй напруженостi, дотичнi до яких в кожнiй довiльнiй точцi спiвпадають з напрямом

Рис. № 39:

51

вектора напруженостi електростатичного поля.

Лiнiї напруженостi (силовi лiнiї) переривчастi: вони починаються в додатнiх зарядах i закiнчуються у вiд’ємних (рис. 38). Це є ознакою того, що електростатичне поле є потенцiальним.

3.1.4 Потiк вектора напруженостi електростатичного поля

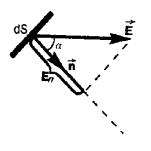
Потiк ветора dΦ, пропорцiйний густинi лiнiй напруженостi поля, якi проходять крiзь деяку площадку dS (рис. 39), орiєнтовану довiльно до лiнiй напруженостi поля, визначається як ска-

лярний добуток векторiв ~ i ~ E dS

dΦE = E→ d→S =
= E dS cos α = En dS,	(212)

→

де вектор dS спрямований вздовж оди-

→

ничної нормалi n до площини dS i по модулю дорiвнює площi dS; α – кут мiж

векторами ~ i ; – проекцiя вектора

→ E ~n En

E (рис. 41) на напрям нормалi до пло-

щадки dS.

Для довiльної замкнутої поверхнi S потiк ΦE

→

вектора E крiзь дану поверхню визначається пiсля iнтегрування по поверхнi S

ΦE = I	E→ d→S = I	En dS .	(213)
S	S
3.1.5 Принцип суперпозицiї		електростатичних
полiв

Рис. № 40:

Якщо електростатичне поле в деякiй точцi утво-

рюється сукупнiстю точкових зарядiв, число

→

яких дорiвнює k, сумарна напруженiсть поля E

52

→

в цiй точцi є векторна сума пружностей полiв Ei, якi окремо утворюються кожним точковим зарядом

E~ =		k	~				F~i.	(214)
	E~i = P		=		1	k
k		i	Fi
X						X
i		Q0			Q0	i

3.1.6 Теорема Остроградського-Гауса

Рис. № 41:

Потiк ΦE вектора напруженостi електростатичного поля E, яке утворюється точковим зарядом Q, крiзь сферичної форми замкнуту поверхню S радiусом r, в центрi якої розташований заряд Q (рис. 42), дорiвнює

	ΦE = I	E→ d→S = E dS cos α =
	S
I	En dS = En I			4πr2Q		Q		(215)
			dS =		=		.
				4πε0εr2		ǫ0ǫ
S		S

Якщо деяка сукупнiсть N зарядiв Qi охоплена замкнутою поверхнею A довiльної форми (рис. 42), потiк вектора напруженостi поля ΦE буде дорiвнювати

N	Qi		(216)
ΦE = iP	,
=1

ǫ0ǫ

де N – кiлькiсть зарядiв, якi охопленi замкнутою поверхнею A. У загальному випадку, коли довiльна поверхня охоплює заряд, який рiвномiрно розповсюджений у деякому об’ємi з деякою густиною ρ = dQ/dV , потiк вектора напруженостi електростатичного поля є

53

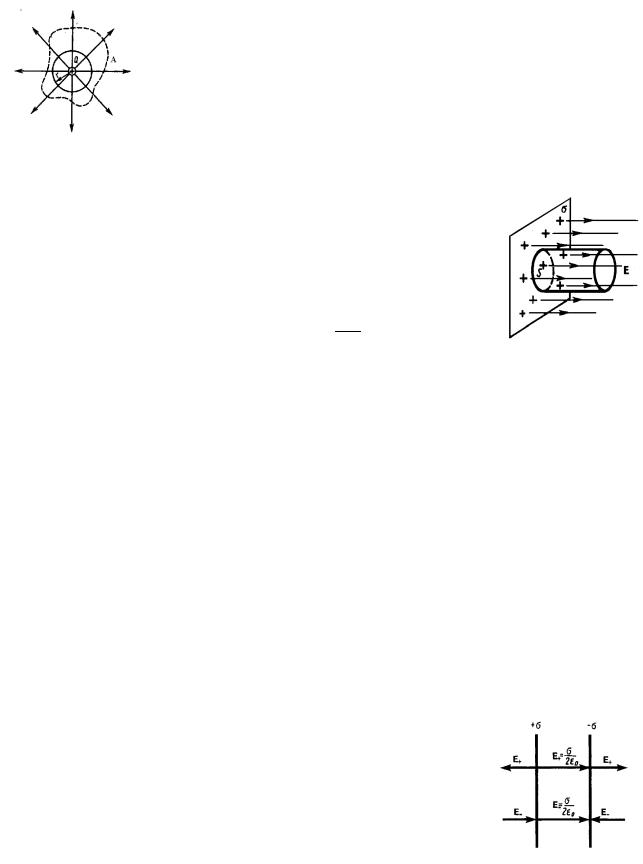
	Рис. № 42:	1
	ΦE =		Z	ρdV.	(217)
		ǫ0 ǫ
			V

Теорема Остроградського-Гауса дозволяє визначити мо-

дуль вектора напруженостi поля ~ :

E

1. Бiля нескiнченної рiвномiрно зарядженої поверхнi з поверхневою густиною заряду σ = ddQS . Якщо на на цiй поверхнi видiлити круглу площадку S, яка є основою для цилiндра, потiк ΦE вектора напруженостi електричного

поля ~ крiзь поверхню цилiндра визначається як потiк

E

вектора ~ крiзь двi площi , якi складають основи видi-

E S

леного цилiндра (рис. 43), оскiльки вектор ~ завжди є

E

перпендикулярним до нескiнченної зарядженої поверхнi i потiк крiзь боковi поверхнi цилiндра дорiвнює нулю. Отже потiк ΦE дорiвнює

ΦE = E S .

Виходячи з теореми Остроградського-Гауса, маємо

Рис. № 43:

(218)

ΦE

=

Q

=

σ S

.

(219)

ε 0ε

ε0ε

Пiсля порiвняння правих частин виразiв (218) i (219) отримаємо

σ S

σ

(220)

E S =

.

E =

.

ε0ε

2 ε0ε

2. Мiж двома нескiнченними рiвномiрно зарядженими

поверхнями (рис. 44) до протилежних знакiв з поверхне-

вою густиною заряду σ =

dQ

. Зрозумiло, що поле мiж

dS

двома пластинами буде в два рази бiльше, нiж бiля однiєї

поверхнi

σ

Рис. № 44:

(221)

E =

.

ǫ ǫ

0

54

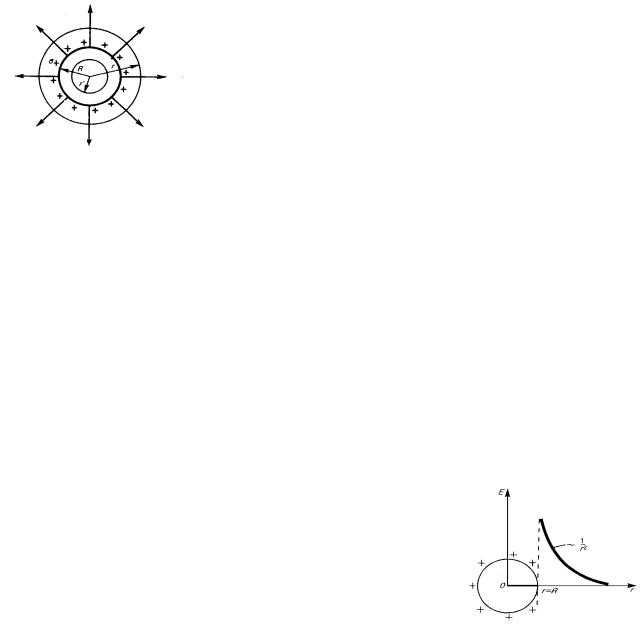
3. На довiльнiй вiдстанi r вiд центра кулi радiусом R (рис. 45), яка утримає заряд Q лише на поверхнi кулi. Потiк ΦE вектора напруженостi поля крiзь замкнуту сфе-

ричну поверхню радiусом r, в центрi якої розташована заряджена куля, буде дорiвнювати, коли R < r

ΦE = E 4 π r2 .

(222)

Виходячи з теореми Остроградського-Гауса, маємо

ΦE =	Q	.	(223)
	ε0ε

Порiвнюючи вираз (222) з (223), якi мають однаковi лiвi частини, отримаємо

E 4 π r2 =	Q	.	(224)
	ε0ε

Звiдки, поле E, яке утворює заряджена куля на вiдстанi r вiд її центра, дорiв-

нює Рис. № 45:	1		Q
E =				(r ≥ R),	(225)
	4π ǫ0ǫ r2
i
E = 0			(r < R) .		(226)

Залежнiсть поля E вiд r представлена на рис. 46.

4. Поле на вiдстанi r′ вiд центра кулi радiусом R, яка утримує заряд Q′, що рiвномiрно розподiлений по об’єму V кулi (ρ = dQ′/dV ). Потiк ΦE вектора напруженостi поля крiзь сферичну поверхню радiуса r′, в центрi якої знаходиться заряджена куля у випадку,

коли r′ > R, дорiвнює
ΦE = E 4π(r′)2 .		(227)
Виходячи з теореми Остроградського-Гауса, потiк ΦE дорiвнює
ΦE =	Q′	=	ρV	.	(228)
	ε0ε
			ε0ε

З порiвняння виразу (227) з (228) у випадку, коли r′ > R, знайдемо поле E

E 4π(r′)2 =	ρV		E =	ρV	,Рис. № 46: (229)
	ε0ε			ε0ε4π(r′)2

55

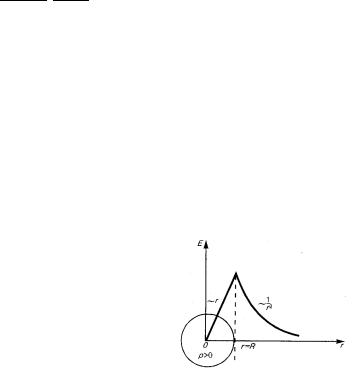
де V = (4/3)πR3. Враховуючи те, що ρ = Q′/((4/3)πR3), вираз (229) можна переписати у виглядi

1 Q′	(230)
E = 4π ǫ0ǫ (r′)2 (r > R).

i залежнiсть E(r′) для r′ > R спiвпадає з залежнiстю (225) для поля, яке утворюється кулею, що заряджена поверхнево.

Для випадку, коли r′ < R, потiк поля вiд зарядiв, якi знаходиться зовнi сфери радiусом r′, дорiвнює нулю, а заряд Q′′ у внутрiшнiй частинi сфери радiусом r′, який дорiвнює Q′′ = ρ (4/3)π(r′)3, утворює потiк

ΦE

ΦE = E · 4π(r′)2 .

(231)

Виходячи з теореми Остроградського-Гауса, потiк дорiвнює

ΦE =	Q′′	=	ρ (4/3)π(r′)3	.	(232)
	ε0ε
			ε0ε

Прирiвнявши правi частини виразiв (231) i (232), i врахувавши те, що ρ = Q′/((4/3)πR3), отримаємо

									Рис. № 47:
		ρ (4/3)π(r′)3							Q′
E · 4π(r′)2 =								E =		r′	(233)
					ε0ε				4πε0ε R3
Залежнiсть поля E вiд r′ представлена на рис. 47.
5. Поле на вiдстанi r вiд осi нескiнченно довгово
цилiндра (нитi) радiусом R, що рiвномiрно вздовж
поверхнi нитi заряджена з лiнiйною густиною заряду
τ = dQ/dl (заряд внутрi нитi дорiвнює нулю),
1				τ				(234)
Eнитi =					(r ≥ R) .
	4π ǫ0ǫ			r
Оскiльки заряд у внутрiшнiй частинi нитi дорiвнює

нулю, внутрiшнє поле дорiвнює нулю
Eнитi = 0 (r < R)	(235)

i залежнiсть поля E вiд r подiбна тiй, що наведена на рис. 46, де E 1/r для r ≥ R.

56

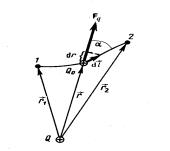
3.1.7 Робота по перемiщенню заряду в електростатичному полi

Елементарна робота dA по перемiщенню пробного заряду Q0 є робота сили Кулона з боку заряду Q, який утворює електричне поле, що дорiв-

→

нює скалярному добутку сили Кулона

Fq та векто-

ра

перемiщення

→

dl

dA = F→q d→l = Fq dl cosα =

1

Q Q

0

dl cosα .

4π ǫ0 ǫ

r2

(236)

Враховуючи те, що dl cosα = dr, отримаємо

dA = Fq dl cosα =

1

Q Q0

dr .

(237)

4πǫ0 ǫ

r2

Повна робота сили Кулона по перемiщенню заряду

Q0 з точки 1 в точку 2 (рис. 48) дорiвнює

r2

Q Q

r2

dr

A12 = Z

dA =

0

Z

(238)

4πǫ0 ǫ

r2

r1

r1

A12

=

Q Q0

1

1

! .

(239)

4πǫ0 ǫ

r1 − r2

Тобто, работа, що виконує сила Кулона (внутрiшня сила замкнутої системи), не залежить вiд форми шляху, а визначається лише положенням початкової та кiнцевої точок траєкторiї. Це є ознакою того, що електростатичне поле є потенцiальним.

3.1.8 Циркуляцiя вектора напруженостi електростатичного поля

Виходячи з останнього виразу, робота A1−2−1 по пе-
ремiщенню пробного заряду Q0 по замкненiй траєкторiї
довiльної форми (r1 = r2) дорiвнює нулю
A1−2−1 = I	dA = 0 .	(240)
L
Дiйсно, повертаючись назад, до визначення роботи
A1−2−1 по перемiщенню пробного заряду Q0 полем вздо-
вж замкнутої траєкторiї (позначеною як L = 1 −2 −1),			Рис. № 48:

57

отримаємо

	I F→ d→l = Q0 I E→ d→l =
	L		L
		2		1
	= Q0 Z E~ d~l + Q0 Z E~ d~l =
		1		2
		2	− Q0	2
	= Q0	Z E~ d~l		Z E~ d~l ≡ 0 ,	(241)
де iнтеграл I E→ d→l = I		1		1
		El dl називається циркуляцiєю вектора елек-
L	L			→
					дорiвнює нулю,
тростатичного поля i той факт, що циркуляцiя вектора E

є ознакою того, що електростатичне поле є потенцiальним.

3.1.9Потенцiальна енергiя заряду в електростатичному полi

Виходячи з того, що електростатичне поле є потенцiальним, робота консервативних (внутрiшнiх), в даному випадку, кулонiвських сил можна представити як рiзницю потенцiальних енергiй W1, 2 пробного заряду Q0 в точках

					→		→
1 i 2, якi характеризуються векторами r1						i r2. Тобто
A1−2 =	1		Q Q0	−	1			Q Q0	= W1	− W2 .	(242)
	4πǫ0 ǫ		r1		4πǫ0 ǫ			r2

Дiйсно, робота консервативних сил для перемiщення пробного заряду Q0 в потенцiальному електростатичному полi повинна дорiвнювати рiзницi потенцiальних енергiй W1 −W2 заряду в початковiй (1) та кiнцевiй (2) точках поля, то

A1−2 = W1 − W2 .

(243)

Звiдки потенцiальна енергiя, яку має пробний заряд Q0 в деякiй точцi поля, визначається з точнiстю до константи

W =	1		Q Q0	+ C,	(244)
	4πǫ0 ǫ		r

де Q – заряд, який утворює електростатичне потенцiальне поле. Константа C у виразi (244) дорiвнює нулю (C = 0), бо на нескiнченностi (r = ∞) потенцiальна енергiя пробного заряду дорiвнює нулю (W∞ = 0).

Якщо електростатичне поле утворюється сумою зарядiв Qi, то потенцiальна енергiя пробного заряду Q0 буде

	Q0	k	Qi		,	(245)
W =		X
	4π ǫ ǫ	i	r	i
0

58

де ri – радiуси-вектори, якi починаються в зарядах Qi i закiнчуються в точцi, де визначається сумарна потенцiальна енергiя пробного заряду.

3.1.10Потенцiал електростатичного поля

Потенцiал електростатичного поля ϕ в деякiй довiльнiй точцi поля є скалярна величина, яка дорiвнює вiдношенню потенцiальної енергiї пробного заряду до величини цього заряду

	W		1		k	Qi		,	(246)
ϕ =			=		X
	Q	0		4πǫ ǫ	i	r	i
			0

i яка не залежить вiд величини пробного заряду Q0.

Виходячи з визначення рiзницi потенцiальної енергiї пробного заряду в точках (1) i (2) (вираз (243)), рiзниця потенцiалiв dϕ = ϕ2 − ϕ1 мiж двома

точками поля (1) i (2) дорiвнює скалярному добутку векторiв ~ i ~ , початок

E dl

якого знаходиться у точцi (1), а кiнець – у точцi (2),

	dA1	2		F~ , d~l	~ ~
dϕ =	Q0−		=	Q0	= E, dl

Тобто

~ ~

dϕ = El, dl .

= (El, dl) . (247)

(248)

Пiсля iнтегрування правої та лiвої частин рiвняння (248) в межах, що вiдпо-

вiдають точкам (1) та (2), отримаємо, що рiзниця потенцiалiв			ϕ, дорiвнює
2	2
ϕ1 − ϕ2 = − ϕ = − Z	E→ d→l = − Z	Eldl .	(249)
1	1

Формула (249) дозволяє визначити рiзницю потенцiалiв ϕ мiж двома будьякими точками електростатичного поля, для якого вiдома залежнiсть E(r).

1. Вiдомо, що бiля нескiнченної зарядженої плоскої поверхнi поле E = σ/(2ε0ε) не залежить вiд координати r (однорiдне електростатичне поле).

Тому рiзниця потенцiалiв ϕ мiж двома довiльними точками дорiвнює

ϕ =

−

σ

r2 dr =

−

σ

r r2

=

σ

(r1

−

r2) =

σ

r

(250)

2ε0ε

2ε0ε

2ε0ε

2ε0ε

Z

1

r1

r

i залежить вiд вiдстанi мiж точками.

2. Аналогiчно можна визначити рiзницю потенцiалiв мiж двома зарядженими до протилежних знакiв нескiнченними площинами

	ϕ =	σ	d ,	(251)
		ε0ε

59

де d – вiдстань мiж площинами (плоского конденсатора).

3. Бiля рiвномiрно зарядженої сферичної поверхнi радiусом R з загальним зарядом Q електростатичне поле E зменшується iз зростом r, коли r > R за формулою

	Q	(252)
E =	4πε0ε r2 .

Звiдки рiзниця потенцiалiв ϕ мiж двома довiльними точками, якi характеризуються радiус-векторами ~r1 i ~r2, дорiвнює

Q

r2

1

Q

1

r2

Q 1

1

ϕ =

Z

dr =

!

=

! .

(253)

4 π ε0 ε

2

4 π ε0 ε

−r

4 π ε0 ε r1

r

1

− r2

r1

r

Тобто, потенцiал ϕR на поверхнi зярядженої сфери (r1 = R, r2 = ∞) дорiвнює

ϕR =	Q 1			−	1	! =	Q	.	(254)
	4 π ε0 ε R
					∞ 4 π ε0 ε R

3.1.11Напруженiсть електростатичного поля як градiєнт потенцiалу

Iснує ще одне визначення вектора напруженостi ~ електростатичного поля

E

в деякiй точцi через градiєнт потенцiалу поля ϕ в цiй же точцi, виходячи з того, що електростатичне поле (поле нерухомих зарядiв) є потенцiальним.

За аналогiєю з визначенням сили тяжiння

~

P , що дiє на тiла, якi знаходяться

в потенцiальному полi тяжiння Землi

~

P = −grad Π, виразимо силу Кулона

~

~

Fq i напруженiсть поля E через вiдповiдно потенцiальну енергiю поля W i

потенцiал поля ϕ

F~q =

−

grad W ,

E~ =

F~q

=

−

grad

W

! =

−

grad ϕ .

(255)

Q0

Q0

Тобто,

∂ϕ

∂ϕ

∂ϕ

E→=

−

e→1

+

e→2 +

e→3

! =

−

grad ϕ =

−

ϕ,

(256)

∂x

∂y

∂z

→

→

→

де e1,

e2

i e3 – одиничнi безрозмiрнi вектори, що спрямованi вздовж трьох

координатних осей x, y та z.

3.1.12Еквiпотенцiальнi поверхнi, лiнiї

Поверхнi, або лiнiї, на яких потенцiал залишається незмiнним, називаються

еквiпотенцiальними (рис. 49).

60